八、樹(Tree)
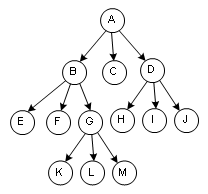
樹,顧名思義,長得像一棵樹,不過通常我們畫成一棵倒過來的樹,根在上,葉在下。不說那么多了,圖一看就懂:
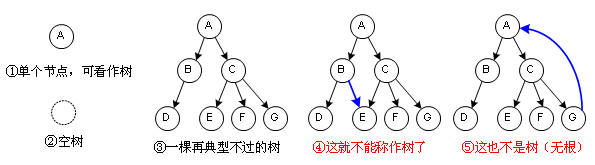
當然了,引入了樹之后,就不得不引入樹的一些概念,這些概念我照樣盡量用圖,誰會記那么多文字?
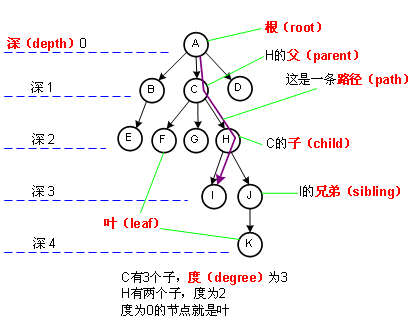
樹這種結構還可以表示成下面這種方式,可見樹用來描述包含關系是很不錯的,但這種包含關系不得出現交叉重疊區域,否則就不能用樹描述了,看圖:
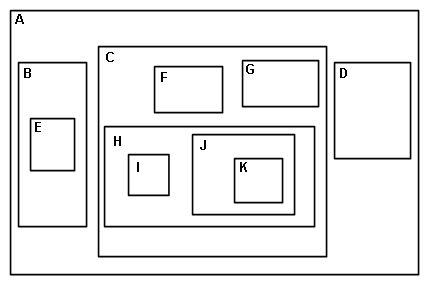
面試的時候我們經常被考到的是一種叫“二叉樹”的結構,二叉樹當然也是樹的一種了,它的特點是除了葉以外的節點都有兩個子,圖:
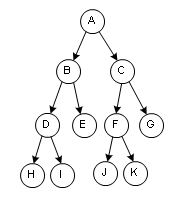
由此我們還可以推出“三叉樹”:
當然還有“四叉樹”,“五叉樹”,“六叉樹”……但太難畫了,節點太多,略過。
九、樹的遍歷(Traversal)
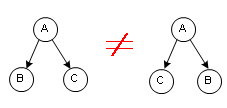
值得再提一下的是二叉樹,因為它確實比較特別,節點有兩個子,這兩個子是有左右之分的,顛倒一下左右,就是不一樣的二叉樹了,所以左右是不能隨便顛倒的。
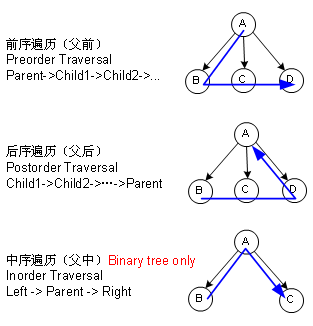
在第三篇講到“隊”的時候,提及到了廣度優先遍歷(Breadth-first traversal),除了廣度優先遍歷之外,還有深度優先遍歷(Depth-first Traversal),深度優先遍歷又可分為:前序遍歷(Preorder Traversal),后序遍歷(Postorder Traversal)和中序遍歷(Inorder Traversal),其中中序遍歷只有對二叉樹才有意義,下圖解釋這幾種遍歷:
好了,又到代碼階段,寫點代碼。我看過許多數據結構的教材,二叉樹遍歷都是必不可少的內容,而且我知道的全部都是用遞歸實現的,現在,我要求你不用遞歸,實現對二叉樹的中序遍歷。怎么辦?我給個提示:廣度優先遍歷時候我們用了隊,中序遍歷,我們使用*棧*。看看能不能寫出來,我也來寫:
#include <stdio.h>
// TreeNode
//////////////////////////////////////////////////////////////////////////
struct TreeNode
{
char m_cVal;
TreeNode* m_pLeft;
TreeNode* m_pRight;
TreeNode(char cVal);
~TreeNode();
};
TreeNode::TreeNode(char cVal)
{
m_cVal = cVal;
m_pLeft = 0;
m_pRight = 0;
}
TreeNode::~TreeNode()
{
}
//Stack
//////////////////////////////////////////////////////////////////////////
class Stack
{
public:
Stack(int iAmount = 10);
~Stack();
//return 1 means succeeded, 0 means failed.
int Pop(TreeNode* &pVal);
int Push(TreeNode* pVal);
int Top(TreeNode* &pVal);
//1 means not null, 0 means null.
int NotNull();
private:
TreeNode **m_ppData;
int m_iCount;
int m_iAmount;
};
Stack::Stack(int iAmount)
{
m_ppData = new TreeNode*[iAmount];
m_iCount = 0;
m_iAmount = iAmount;
}
Stack::~Stack()
{
delete m_ppData;
}
int Stack::Pop(TreeNode* &pVal)
{
if(m_iCount>0)
{
--m_iCount;
pVal = m_ppData[m_iCount];
return 1;
}
return 0;
}
int Stack::Push(TreeNode* pVal)
{
if(m_iCount<m_iAmount)
{
m_ppData[m_iCount] = pVal;
++m_iCount;
return 1;
}
return 0;
}
int Stack::Top(TreeNode* &pVal)
{
if(m_iCount>0 && m_iCount<=m_iAmount)
{
pVal = m_ppData[m_iCount-1];
return 1;
}
return 0;
}
int Stack::NotNull()
{
if(m_iCount!=0)
return 1;
return 0;
}
int main(int argc, char* argv[])
{
//Construct the tree.
// A
// / \
// / \
// B C
// \ / \
// D E F
// \ \
// G H
// / \
// I J
// / \
// K L
TreeNode nA('A');
TreeNode nB('B');
TreeNode nC('C');
TreeNode nD('D');
TreeNode nE('E');
TreeNode nF('F');
TreeNode nG('G');
TreeNode nH('H');
TreeNode nI('I');
TreeNode nJ('J');
TreeNode nK('K');
TreeNode nL('L');
nA.m_pLeft = &nB;
nA.m_pRight = &nC;
nB.m_pRight = &nD;
nD.m_pRight = &nG;
nC.m_pLeft = &nE;
nC.m_pRight = &nF;
nF.m_pRight = &nH;
nH.m_pLeft = &nI;
nH.m_pRight = &nJ;
nI.m_pLeft = &nK;
nI.m_pRight = &nL;
Stack st;
//Inorder traversal
TreeNode *pVal = &nA;
int iPopped = 0;
while(pVal!=0)
{
if(pVal->m_pLeft!=0 && iPopped==0)
{
st.Push(pVal);
pVal = pVal->m_pLeft;
iPopped = 0;
}
else if(pVal->m_pRight!=0)
{
printf("%c ", pVal->m_cVal);
pVal = pVal->m_pRight;
iPopped = 0;
}
else
{
printf("%c ", pVal->m_cVal);
if(0==st.Pop(pVal))
break;
iPopped = 1;
}
}
return 0;
}
代碼就那么一點,可第一次寫的時候我還真覺得頗費腦筋的。代碼中有些注釋顯示不太正常,這是因為這個博客的的代碼字體非等寬的緣故,拿到你的IDE下查看就正常了。
(未完待續……)