七、哈希表（Hash Table）及散列法（Hashing）
數(shù)組的特點是：尋址容易，插入和刪除困難；而鏈表的特點是：尋址困難，插入和刪除容易。那么我們能不能綜合兩者的特性，做出一種尋址容易，插入刪除也容易的數(shù)據(jù)結構？答案是肯定的，這就是我們要提起的哈希表，哈希表有多種不同的實現(xiàn)方法，我接下來解釋的是最常用的一種方法——拉鏈法，我們可以理解為“鏈表的數(shù)組”，如圖：
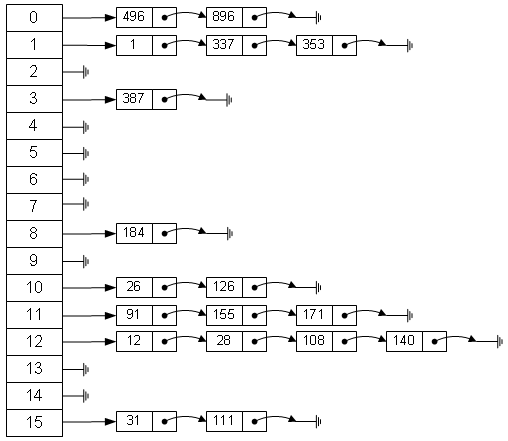
左邊很明顯是個數(shù)組，數(shù)組的每個成員包括一個指針，指向一個鏈表的頭，當然這個鏈表可能為空，也可能元素很多。我們根據(jù)元素的一些特征把元素分配到不同的鏈表中去，也是根據(jù)這些特征，找到正確的鏈表，再從鏈表中找出這個元素。
元素特征轉變?yōu)閿?shù)組下標的方法就是散列法。散列法當然不止一種，我下面列出三種比較常用的。
1，除法散列法
最直觀的一種，上圖使用的就是這種散列法，公式：
index = value % 16
學過匯編的都知道，求模數(shù)其實是通過一個除法運算得到的，所以叫“除法散列法”。
2，平方散列法
求index是非常頻繁的操作，而乘法的運算要比除法來得省時（對現(xiàn)在的CPU來說，估計我們感覺不出來），所以我們考慮把除法換成乘法和一個位移操作。公式：
index = (value * value) >> 28
如果數(shù)值分配比較均勻的話這種方法能得到不錯的結果，但我上面畫的那個圖的各個元素的值算出來的index都是0——非常失敗。也許你還有個問題，value如果很大，value * value不會溢出嗎？答案是會的，但我們這個乘法不關心溢出，因為我們根本不是為了獲取相乘結果，而是為了獲取index。
3，斐波那契（Fibonacci）散列法
平方散列法的缺點是顯而易見的，所以我們能不能找出一個理想的乘數(shù)，而不是拿value本身當作乘數(shù)呢？答案是肯定的。
1，對于16位整數(shù)而言，這個乘數(shù)是40503
2，對于32位整數(shù)而言，這個乘數(shù)是2654435769
3，對于64位整數(shù)而言，這個乘數(shù)是11400714819323198485
這幾個“理想乘數(shù)”是如何得出來的呢？這跟一個法則有關，叫黃金分割法則，而描述黃金分割法則的最經(jīng)典表達式無疑就是著名的斐波那契數(shù)列，如果你還有興趣，就到網(wǎng)上查找一下“斐波那契數(shù)列”等關鍵字，我數(shù)學水平有限，不知道怎么描述清楚為什么，另外斐波那契數(shù)列的值居然和太陽系八大行星的軌道半徑的比例出奇吻合，很神奇，對么？
對我們常見的32位整數(shù)而言，公式：
index = (value * 2654435769) >> 28
如果用這種斐波那契散列法的話，那我上面的圖就變成這樣了：
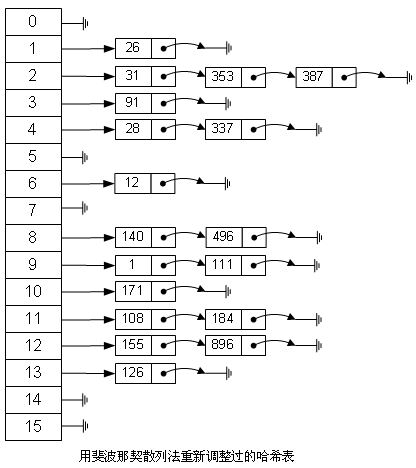
看起來不錯，以后就用斐波那契散列法吧。
不過我們要注意了，前面提到的都是針對整數(shù)的散列法，那如果不是整數(shù)呢？下面給出一些參考算法，我把其它類型的數(shù)據(jù)轉變?yōu)?2位整數(shù)，之后的處理前面已經(jīng)說了。
1，浮點數(shù)的散列法
unsigned int HashingDouble(double d)
{
if (d==0)
return 0;
else
{
int exponent;
double mantissa = frexp(d, &exponent);
return (unsigned int)((2*mantissa-1) * (~0U));
}
}
2，字符串的散列法
unsigned int HashingString(char *str, int iLen)
{
unsigned int hsval = 2654435769;
int i;
int iShift = 0;
for(i=0; i<iLen; i++)
{
hsval ^= (str[i]<<iShift);
iShift+=3;
if(iShift>24)
iShift=0;
}
return hsval;
}
方法就提供那么多，遇到別的情況，比如說Unicode字符串，隨機應變吧！