五、隊(Queue)
前一篇講了棧(Stack),隊和棧其實只有一個差別,棧是先進后出,隊是先進先出,如圖:
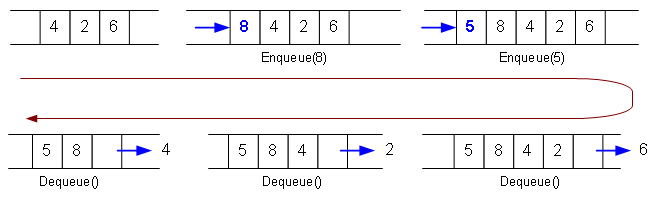
從圖中可以看出,隊有兩個常用的方法,Enqueue和Dequeue,顧名思義,就是進隊和出隊了。隊和棧一樣,既可以用數組實現,也可以用鏈表實現,我還是偏向于用數組,我的實現示意圖如下:
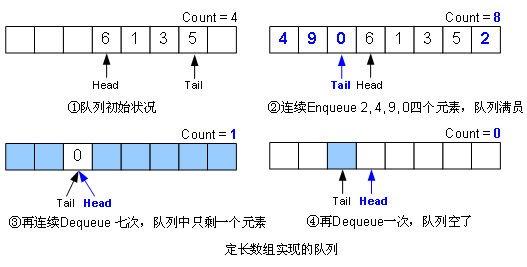
隊有啥用呢?一個最常用的用途就是“buffer”,即緩沖區,比如有一批從網絡來的數據,處理需要挺長的時間,而數據抵達的間隔并不均勻,有時快,有時慢,先來的先處理,后來的后處理,于是你創建了一個隊,用來緩存這些數據,出隊一筆,處理一筆,直到隊列為空。當然隊的作用遠不止于此,下面的例子也是一個很經典的例子,希望讀者能舉一反三。
例子:使用隊對樹進行廣度優先遍歷。
廣度優先區別于深度優先,即優先遍歷最靠近根節點的各個節點:

我們的算法是:
1,根節點入隊
2,出隊一個節點,算一次遍歷,直到隊列為空
3,將剛出隊的節點的子節點入隊
4,轉到2
隊列的狀況如下圖:
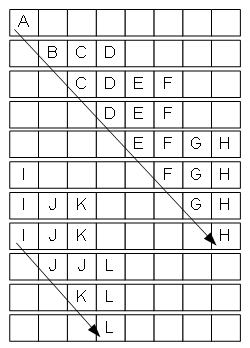
樹的遍歷一般習慣使用遞歸,理論上所有的遞歸都可以轉變為迭代,如何實現這個轉變?隊就是其中一種有效的辦法,OK,下面我給出上述例題的代碼以及注釋。
//Not grace code but enough for demo. ^_^
#include "stdio.h"
// The Node
//////////////////////////////////////////////////////////////////////////
struct Node
{
Node(char cChar, int iSubNodeNum=0);
~Node();
char m_cChar;
int m_iSubNodeNum;
Node** m_arrNodePointer; //Pointers to the sub-node.
};
Node::Node(char cChar, int iSubNodeNum)
{
m_cChar = cChar;
m_iSubNodeNum = iSubNodeNum;
if(iSubNodeNum!=0)
m_arrNodePointer = new Node*[iSubNodeNum];
else
m_arrNodePointer = NULL;
}
Node::~Node()
{
if(m_arrNodePointer!=NULL)
delete[] m_arrNodePointer;
}
// The Queue
//////////////////////////////////////////////////////////////////////////
class Queue
{
public:
Queue(int iAmount=10);
~Queue();
//return 0 means failed, return 1 means succeeded.
int Enqueue(Node* node);
int Dequeue(Node* & node);
private:
int m_iAmount;
int m_iCount;
Node** m_ppFixed; //The pointer array to implement the queue.
int m_iHead;
int m_iTail;
};
Queue::Queue(int iAmount)
{
m_iCount = 0;
m_iAmount = iAmount;
m_ppFixed = new Node*[iAmount];
m_iHead = 0;
m_iTail = iAmount-1;
}
Queue::~Queue()
{
delete[] m_ppFixed;
}
int Queue::Enqueue(Node* node)
{
if(m_iCount<m_iAmount)
{
++m_iTail;
if(m_iTail > m_iAmount-1)
m_iTail = 0;
m_ppFixed[m_iTail] = node;
++m_iCount;
return 1;
}
else
return 0;
}
int Queue::Dequeue(Node* & node)
{
if(m_iCount>0)
{
node = m_ppFixed[m_iHead];
++m_iHead;
if(m_iHead > m_iAmount-1)
m_iHead = 0;
--m_iCount;
return 1;
}
else
return 0;
}
// Main
//////////////////////////////////////////////////////////////////////////
int main(int argc, char* argv[])
{
//Construct the tree.
Node nA('A', 3);
Node nB('B', 2);
Node nC('C');
Node nD('D', 3);
Node nE('E');
Node nF('F', 2);
Node nG('G');
Node nH('H', 1);
Node nI('I');
Node nJ('J');
Node nK('K');
Node nL('L');
nA.m_arrNodePointer[0] = &nB;
nA.m_arrNodePointer[1] = &nC;
nA.m_arrNodePointer[2] = &nD;
nB.m_arrNodePointer[0] = &nE;
nB.m_arrNodePointer[1] = &nF;
nD.m_arrNodePointer[0] = &nG;
nD.m_arrNodePointer[1] = &nH;
nD.m_arrNodePointer[2] = &nI;
nF.m_arrNodePointer[0] = &nJ;
nF.m_arrNodePointer[1] = &nK;
nH.m_arrNodePointer[0] = &nL;
Queue que;
que.Enqueue(&nA);
Node *pNode;
while (que.Dequeue(pNode)==1)
{
printf("%c ", pNode->m_cChar);
int i;
for(i=0; i<pNode->m_iSubNodeNum; i++)
{
que.Enqueue(pNode->m_arrNodePointer[i]);
}
}
return 0;
}
代碼不算通用,但用來演示和理解足夠了,下一篇的內容更精彩!
(未完待續……)