Welcome to ErranLi's Blog!

原文：http://www.cnblogs.com/JCSU/articles/1490363.html

?

一、用矩陣運算法解線性方程組

?

1、矩陣運算規則及MATLAB實例

?

(1)? 矩陣加(減)法：即兩矩陣對應元素相加減，要求兩矩陣的階數必須相同。

??????C = A + B

?

(2)? 矩陣乘法：m×p階矩陣A與p×n階矩陣B的乘積C是一個m×n階的矩陣。元素C(i, j)的值為A矩陣的第i行和B矩陣的第j列對應元素乘積的和。

??????A*B = C

????? 矩陣乘法一般不滿足交換律，即：A*B ≠ B*A

例：

?

?

(3)? 矩陣求逆：矩陣的逆陣V定義為滿足V*A = I (I為與A同階的單位矩陣)。只有方陣才可以求逆，而且此方陣的行列式必須不為零，det(A) ≠ 0。如果det(A)?= 0，求逆時就會出現無窮大，此時的矩陣稱為奇異的。

例：

?

?

(4)? 矩陣轉置：矩陣的行列互換后構成轉置矩陣。如果A是m×n階的，則A^T是n×m階的。

例：

?

?

(5)? 矩陣分塊：矩陣A可以劃分成許多小矩陣。

例：

?

?

(5)? 矩陣分解為向量：把矩陣沿行向或列向分解為單列或單行向量，常見的是分解為列向量。

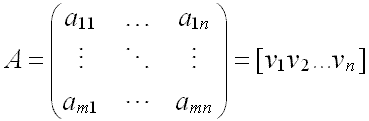
其中：

?

?

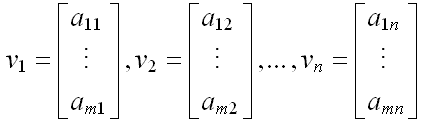
(6)? 行向量左乘列向量：要求兩向量的長度必須一致，結果為一個標量。得出的是向量各分量的平方和。如果這些分量是正交的，則得出的是向量的長度平方。它的平方根就是向量長度，也稱為向量的范數或2范數。

行向量左乘列向量得到的是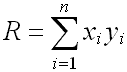，在工程中具有這樣計算形式的問題很多，比如用它計算兩個向量x和y之間的相關性。

?

(7)? 列向量左乘行向量：如果列向量的長度為n，行向量的長度為m，則相乘會得出一個n×m的矩陣，這種方法常常用來生成和計算一些復雜的大矩陣。

?

(8)? 矩陣乘法和冪次：A^2 = A*A,? A^n =? A*A*...*A。根據矩陣相乘內階數必須相等，只有方陣才能乘方和冪次。

?

?

2、初等變換乘子矩陣的生成及MATLAB實例

?

本節通過將原矩陣左乘變換的單位矩陣實現矩陣的初等行變換：

(1) 行交換：將矩陣A的第 i , j 兩行互換位置。

?

寫成函數E1gen(A,i,j)：

?

?

(2) 行乘數：將矩陣A的第 i 行乘以 k 。

?

?

寫成函數E2gen(A,i,k)：

?

?

?

(3) 行相加：將矩陣的第 i 行乘以 k，加到第 j 行。

?

寫成函數E3gen(A,i,j,k)：

?

?

實例：

要消去下列矩陣的A(2,1)，求乘子矩陣E3

?

在第二行加以第一行乘 -A(2,1)/A(1,1) = -2，故令E3 = E3gen(A,1,2,-2)

?

綜上可知：

1、 行階梯生成等價于矩陣左乘

因此，整個行階梯形式U的生成過程，可以看作把原矩陣左乘以一系列的初等變換矩陣E1和E3。把這些初等矩陣的連乘積寫成EX，則有:?U=EX*A，設其逆為L:

從而有 L*U=A?

就是說，A可以分解為一個準下三角矩陣L和一個上三角（即行階梯）矩陣U的乘積。MATLAB提供了三角分解的函數lu，它的調用方法是：[L,U]=lu(A)

2、 lu分解是求行階梯的一個方法

用lu函數求出的U實際上就是A的行階梯形式（不是簡化行階梯形式）。所以，求簡化行階梯形式用rref函數，而求行階梯形式可以用lu 函數。不過，它和我們用消元運算所得U的數據不一定相同，盡管得出的階次和階梯形狀相同。但因為行階梯形式可以有無數種，用不同步驟算出的結果也不同。只有變成簡化行階梯形式，才能進行比較，看它是不是惟一的。

?

?

3、行列式

(1) 行列式的幾何意義：

行列式的幾何意義是面積或體積，它的用途很單一，就是判斷奇異性，連正負號都不必關心。

(2) 行列式的計算方法：

計算行列式的最好方法還是行階梯法，可以利用lu分解
??????????????? [L,U] = lu(A)
把A分解為一個準下三角矩陣L和一個上三角矩陣U的乘積。因為det(L) = 1，所以U和A的行列式相等。??

?????????????? det(A) = det(U)
而三角矩陣U的det(U)很好求。只要把U的主對角線元素連乘就可得到它的行列式。

?

實例：

?

用det求A的行列式值得到相同的結果：

?

?

?

4、矩陣的秩和矩陣求逆

?

矩陣的秩：

(1) 按定義，矩陣的秩是矩陣A中行列式不等于零的最高階子式的階次。是用以衡量聯立方程中有效方程數目的指數。
(2) 按照定義來計算矩陣的秩，可能遇到的問題也是子矩陣的數量很大，每個矩陣的行列式計算又非常麻煩，其計算量也將是不可接受的天文數字。
(3) 計算矩陣的秩的最好方法是行階梯法，行階梯化簡后非全為零的行數就是該矩陣的秩。用MATLAB函數r=rank(A)可以檢驗A的秩，rank函數對A是否是方陣沒有要求，即可以有m≠n。

?

矩陣求逆：

(1) 對于n×n方陣A，當r=n時，稱A是滿秩的，若r<n，必有det(A) = 0，稱A是欠秩的或奇異的。奇異矩陣不可以求逆。?
(2) 矩陣求逆的最簡單方法也是行階梯化簡，其方法是設定一個由A和I組成的增廣矩陣C = [A,I]，求C的簡化行階梯形式UC = rref([A,I])，得出UC = [I,V]。V就顯示出這個逆矩陣的內容。

?

求逆實例：

?

矩陣求逆命令：V=inv(A)

?

?

5、條件數—衡量奇異程度的量

(1) 在用數值方法計算矩陣的逆時，由于計算中的誤差，人們不大可能得到理想的零合理想的全零行，所以矩陣是否奇異，并不是那么絕對的。
(2) 為了評價矩陣接近‘奇異’的程度，采用了‘條件數’（Condition Number）作為常用的衡量指標。它永遠大于1。其數值愈接近于1，計算誤差愈小。
(3) MATLAB中，條件數用cond(A)計算，它達到10的4次方以上時，求逆的誤差就可能相當可觀。像現在，條件數達到10的16次方（注：條件數是逆條件數RCOND的倒數），結果是根本不能用的。

?

6、用矩陣‘除法’解線性方程

?

(1) 如果m = n，則線性代數方程Ax = b中的A是方陣，設det(A)≠0，則它的逆陣存在。將上式左右同乘以inv(A) ，由于inv(A)*A = I，得到

X = inv(A)*b （1）

MATLAB創立了矩陣除法的概念，因為 inv(A)相當于將A放到分母上去，所以可以把上式寫成

X = A \ b????? （2）

‘\’就稱為左除，因為inv(A)是乘在b的左方。

?

(2) 左除’\’解線性方程的擴展

左除‘\’的功能遠遠超過了矩陣求逆函數inv，inv(A)函數要求A必須是方陣，所以（1）式只能用來解‘適定’方程，而（2）式并不要求A為方陣，在A是m×n階且m < n（欠定）時，它只要求A與b的行數相等且A的秩為m。所以（2）式也可以用來解欠定方程，在下例中可以看出。此外，運算符‘\’還能用來解超定方程。

?

例：左除’\’解欠定方程

?

得到x=inf，無解。改用行階梯方法找有效行。左除要求的是系數矩陣的行數與秩相同

?

其中，x是此欠定方程的一個特解。

?