首先，要再現bug得先準備bug條件，使用Windows下的Dev-C++按照目錄下bin文件夾下面的c和c++編譯器和鏈接器，可以直接使用Dev-C++，或者用CodeBlocks然后編譯鏈接的目錄設置為Dev-C++的bin目錄。這個bug是在今天月賽時候出現的，我用%lld讀入一個不大的整數后，再for循環讀入其它一些數字，發現無論如何輸出不了，而我用cin和cout操作longlong的時候，超時1倍多，很惡心的出題人，本來就是一個水題，居然做成這樣。然后沒辦法，快結束的時候，問旁邊的隊友，因為是個人賽，所以是自己在做，longlong，如何讀入，他說%lld。是啊，我一直這樣讀，這樣輸出，為啥出問題了。。。沒辦法照著他的樣子，把輸入改成了int，直接%d讀入，答案還是longlong，再%lld輸出就沒超時了，真惡心的一天啊。
64位本來就用得不多，而且對于大多數Windows下的用戶，基本都是vc6和vs08什么的。vs08我已經實驗過，不會出現這個bug，PS：是完全一樣的代碼，親自單步調試實驗的，無任何bug。vc6只能用%I64d輸入和輸出。那么，問題就只是在Dev-C++的用戶中存在了。 回來的時候，我就決心找出問題的所在。所以，我打算升級g++的版本。下了個Dev-C++ 5.0也沒用，和前面的Dev-C++ 4.9.9.2一樣的，惡心啊。
然后google+百度了很久，發現CSDN上一篇博文解釋說，這就是Dev-C++自己的事情。因為gcc本來是linux下的，所以longlong在自己家里是不會出現問題的。而Dev-C++是把人家移植過來的，那篇博文說Dev-C++的編譯和鏈接器是mingw32-g++.exe，但是Mingw32在編譯期間使用gcc的規則檢查語法，在連接和運行時使用的卻是Microsoft庫。這個庫里的printf和scanf函數當然不認識linux gcc下"%lld"和"%llu"，對"%I64d"和"%I64u"，它則是樂意接受的。Mingw32在編譯期間使用gcc的規則檢查語法，在連接和運行時使用的卻是Microsoft庫。這個庫里的printf和scanf函數當然不認識linux gcc下"%lld"和"%llu"，對"%I64d"和"%I64u"，它則是樂意接受的。意思是，程序里面實質的二進制代碼可能是微軟的庫，只解析%I64d,然后就可能出錯了。具體是什么原因，只有開發Dev-C++的人知道了。或者其它高人。。。
#include <stdio.h>
#include <iostream>
using namespace std;
int main()
{
long long nN;
long long nX, nY;
if (scanf("%lld", &nN) != EOF)
{
printf("nN:%lld\n", nN);
for (
long long i = 0; i < nN; ++i)
{
printf("nN:%lld i:%lld\n", nN, i);
}
getchar();
printf("Over\n");
}
return 0;
}
該代碼會一直死循環，大家可以試試
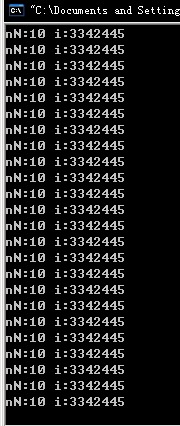
如果改成下面這樣，還可以看到輸入的數據都沒有到達指定的變量
#include <stdio.h>
#include <iostream>
using namespace std;
int main()
{
long long nN;
long long nX, nY;
if (scanf("%lld", &nN) != EOF)
{
printf("nN:%lld\n", nN);
for (long long i = 0; i < nN; ++i)
{
printf("nN:%lld i:%lld\n", nN, i);
scanf("%lld %lld", &nX, &nY);
printf("nX:%lld nY:%lld\n", nX, nY);
}
getchar();
printf("Over\n");
}
return 0;
}
鏈接:
http://poj.grids.cn/practice/2774
這個題可以用二分解,雖然也有dp的解法。可能用二分解這個題不是很明顯,但是確實是可以的。最大的解就是所有的棍子長/要求的棍子數,最小的解是0,直接在其中進行二分即可。這個題屬于二分出最大滿足條件的解的情況。這個題為什么能夠二分了。我是這樣想的。首先,解空間確實是有序的吧,從數字0-數字nSum/nK。其次,對于任意一個處于這個范圍內的數字,只有滿足和滿足題目要求2種情況,那么和我們二分數字有什么區別了,我們二分一個有序數組,看里面有沒有某個數字,是不是也只要判斷下nMid滿足是否條件是吧。所以,這個題是可以二分的。二分的條件就是解空間有序的,或者可以方便在解空間里面跳躍。而且這個題的二分還需要點技巧,因為是查找滿足條件的最大解。
代碼:
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define MAX (10000 + 10)
using namespace std;
int nN, nK;
int nWoods[MAX];
bool IsAnsOk(int nAns)
{
if (nAns == 0)
{
return true;
}
else
{
int nTotal = 0;
for (int i = nN - 1; i >= 0; --i)
{
nTotal += nWoods[i] / nAns;
if (nTotal >= nK)
{
return true;
}
}
return false;
}
}
int SearchAns(int nMax)
{
int nBeg = 0, nEnd = nMax;
while (nBeg <= nEnd)
{
int nMid = (nBeg + nEnd) / 2;
if (IsAnsOk(nMid))
{
nBeg = nMid + 1;
}
else
{
nEnd = nMid - 1;
}
}
return nBeg - 1;
}
int main()
{
while (scanf("%d%d", &nN, &nK) == 2)
{
int nSum = 0;
for (int i = 0; i < nN; ++i)
{
scanf("%d", &nWoods[i]);
nSum += nWoods[i];
}
sort(nWoods, nWoods + nN);
int nMax = nSum / nK;
printf("%d\n", SearchAns(nMax));
}
return 0;
}
所以,只是把==換成了IsAnsOk函數調用而已...而且由于這是查找最大解,返回值做了下變化而已...
仔細分析二分的寫法(我的另一篇文章(標題是關于密碼的一個解題報告)有說明),
其實寫出查找最大解和最小解的二分都不是件麻煩的事情...
鏈接:
http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1219
這個題就是求出所有結點的距離之后,再找出某個結點,該結點離其它結點的最大距離是所有結點中是最小的...
解法1:深搜出所有結點間的距離,但是會超時,即使深搜的過程使用中記憶化搜索(就是用2維數組保存已經搜出的答案,如果后面的搜索需要用到直接使用即可)...
解法2:Floyd算法,3重循環直接找出所有結點之間的最短距離
解法3:對每一個結點應用一次迪杰斯特拉算法,找出所有結點與其它結點間的最短距離...
解法2:
#include <stdio.h>
#include <string.h>
#define MAX (100 + 10)
#define INF (1000000 + 10)
int nN, nM;
int nDis[MAX][MAX];
void SearchAll()
{
for (int k = 0; k < nN; ++k)
{
for (int i = 0; i < nN; ++i)
{
for (int j = 0; j < nN; ++j)
{
if (nDis[i][k] + nDis[k][j] < nDis[i][j])
{
nDis[i][j] = nDis[j][i] = nDis[i][k] + nDis[k][j];
}
}
}
}
}
int main()
{
while (scanf("%d%d", &nN, &nM) == 2)
{
for (int i = 0; i < nN; ++i)
{
for (int j = 0; j < nN; ++j)
{
if (i == j)
{
nDis[i][j] = 0;
}
else
{
nDis[i][j] = INF;
}
}
}
while (nM--)
{
int nX, nY, nK;
scanf("%d%d%d", &nX, &nY, &nK);
nDis[nX][nY] = nDis[nY][nX] = nK;
}
SearchAll();
bool bOk = false;
int nMin = 1 << 30;
for (int i = 0; i < nN; ++i)
{
int nTemp = 0;
int j = 0;
for ( ; j < nN; ++j)
{
if (i == j) continue;
if (nDis[i][j] == INF)
{
break;
}
else
{
if (nDis[i][j] > nTemp)
{
nTemp = nDis[i][j];
}
}
}
if (j == nN)
{
bOk = true;
if (nTemp < nMin)
{
nMin = nTemp;
}
}
}
if (bOk)
{
printf("%d\n", nMin);
}
else
{
printf("Can not\n");
}
}
return 0;
}
關于Floyd算法,可以這樣理解...比如剛開始只取2個結點i,j,它們的距離一定是dis(i,j),但是還有其它結點,需要把其它結點也慢慢加進來,所以最外層關于k的循環意思就是從0至nN-1,把所有其它結點加進來,比如加入0號結點后,距離dis(i,0)+dis(0,j)可能會比dis(i,j)小,如果是這樣就更新dis(i,j),然后后面加入1號結點的時候,實際上是在已經加入0號結點的基礎上進行的處理了,效果變成dis(i,0,1,j),可能是最小的,而且中間的0,1也可能是不存在的,當然是在dis(i,j)原本就是最小的情況下...
這個算法可以用下面這個圖片描述...
解法3:
#include <stdio.h>
#include <string.h>
#define MAX (100 + 10)
#define INF (1000000 + 10)
int nN, nM;
int nDis[MAX][MAX];
void Search(int nSource)
{
bool bVisit[MAX];
memset(bVisit, false, sizeof(bVisit));
bVisit[nSource] = true;
for (int i = 0; i < nN - 1; ++i)
{
int nMin = INF;
int nMinPos = 0;
for (int j = 0; j < nN; ++j)
{
if (!bVisit[j] && nDis[nSource][j] < nMin)
{
nMin = nDis[nSource][j];
nMinPos = j;
}
}
if (bVisit[nMinPos] == false)
{
bVisit[nMinPos] = true;
for (int j = 0; j < nN; ++j)
{
if (nDis[nSource][nMinPos] + nDis[nMinPos][j] < nDis[nSource][j])
{
nDis[nSource][j] = nDis[nSource][nMinPos] + nDis[nMinPos][j];
}
}
}
}
}
void SearchAll()
{
for (int k = 0; k < nN; ++k)
{
Search(k);
}
}
int main()
{
while (scanf("%d%d", &nN, &nM) == 2)
{
for (int i = 0; i < nN; ++i)
{
for (int j = 0; j < nN; ++j)
{
if (i == j)
{
nDis[i][j] = 0;
}
else
{
nDis[i][j] = INF;
}
}
}
while (nM--)
{
int nX, nY, nK;
scanf("%d%d%d", &nX, &nY, &nK);
nDis[nX][nY] = nDis[nY][nX] = nK;
}
SearchAll();
bool bOk = false;
int nMin = 1 << 30;
for (int i = 0; i < nN; ++i)
{
int nTemp = 0;
int j = 0;
for ( ; j < nN; ++j)
{
if (i == j) continue;
if (nDis[i][j] == INF)
{
break;
}
else
{
if (nDis[i][j] > nTemp)
{
nTemp = nDis[i][j];
}
}
}
if (j == nN)
{
bOk = true;
if (nTemp < nMin)
{
nMin = nTemp;
}
}
}
if (bOk)
{
printf("%d\n", nMin);
}
else
{
printf("Can not\n");
}
}
return 0;
}
迪杰斯特拉算法的核心思想是維護一個源點頂點集合,任何最短路徑一定是從這個頂點集合發出的...
初始化時,這個集合就是源點...
我們從該其它結點中選出一個結點,該結點到源點的距離最小...
顯然,這個距離就是源點到該結點的最短距離了,我們已經找到了答案的一部分了...然后,我們就把該結點加入前面所說的頂點集合...
現在頂點集合更新了,我們必須得更新距離了...由于新加入的結點可能發出邊使得原來源點到某些結點的距離更小,也就是我們的源點變大了,邊也變多了,所以我們的最短距離集合的值也必須變化了...
該算法一直循環nN-1次,直至所有的點都加入源點頂點集合...
鏈接:
http://poj.grids.cn/practice/2814
這個題目可以枚舉或者直接暴力。但是,這之前必須弄明白答案的解空間。。。也就是解可能的情況。。。很簡單,一共有9種移動方案。也很了然的知道對于某種方案使用N次的效果等同于N%4的效果,也就是說某種方案只可能使用0,1,2,3次。。。一共有9種方案,那么一共就只有4^9種可能的解。。。這么小的解空間,無論用什么方法都不會超時了。。。暴力可以才用9重循環,或者深搜,當時覺得寫9重循環是件很糗的事情,就果斷深搜了。。。
如果這題才用枚舉的方法的話,思考方式還是那樣先確定假設解的部分情況,通過已經知道的規則確定解的其它情況,然后求出這個解,判斷這個解是否滿足題目要求。。。比如,我們可以枚舉1,2,3號方案的情況,根據規則確定其它方案的使用情況,求出所有方案的使用情況后,判斷假設的解是否滿足要求就可以了...
我才用的是dfs+剪枝,這個題目其實題意或者說答案有誤,因為答案是搜索找到第一個解,而不是所謂的最短序列的解,當然如果數據使得2者都是一樣的話,那么題意就無誤了...我的代碼是假設找到的第一個就是最短序列的,這種情況下才能使用剪枝,因為找到一個解后就不需要繼續找了...
代碼如下:
#include <stdio.h>
int nMinTimes;
int nPath[40];
bool bFind = false;
char* szMoves[10] =
{
NULL,
"ABDE",
"ABC",
"BCEF",
"ADG",
"BDEFH",
"CFI",
"DEGH",
"GHI",
"EFHI"
};
bool IsPosOK(int* nPos)
{
for (int i = 0; i < 9; ++i)
{
if (nPos[i])
{
return false;
}
}
return true;
}
void Move(int nChoose, int nTimes, int* nPos)
{
if (nTimes > 0)
{
char* pszStr = szMoves[nChoose];
while (*pszStr)
{
nPos[*pszStr - 'A'] = (nPos[*pszStr - 'A'] + nTimes) % 4;
++pszStr;
}
}
}
void MoveBack(int nChoose, int nTimes, int* nPos)
{
if (nTimes > 0)
{
char* pszStr = szMoves[nChoose];
while (*pszStr)
{
nPos[*pszStr - 'A'] = (nPos[*pszStr - 'A'] - nTimes + 4) % 4;
++pszStr;
}
}
}
void Cal(int nChoose, int* nPos, int* nUsed, int nUsedTimes)
{
if (nChoose == 10)
{
if (IsPosOK(nPos) && !bFind)
{
nMinTimes = nUsedTimes;
for (int i = 0; i < nMinTimes; ++i)
{
nPath[i] = nUsed[i];
}
bFind = true;
}
return;
}
for (int i = 0; i <= 3; ++i)
{
Move(nChoose, i, nPos);
for (int j = 0; j < i; ++j)//放入i次的nChoose
{
nUsed[nUsedTimes + j] = nChoose;
}
if (!bFind)
{
Cal(nChoose + 1, nPos, nUsed, nUsedTimes + i);
}
MoveBack(nChoose, i, nPos);
}
}
int main()
{
int nPos[9];
int nUsed[40];
for (int i = 0; i < 9; ++i)
{
scanf("%d", &nPos[i]);
}
Cal(1, nPos, nUsed, 0);
for (int i = 0; i < nMinTimes; ++i)
{
printf("%d", nPath[i]);
if (i != nMinTimes - 1)
{
putchar(' ');
}
else
{
putchar('\n');
}
}
return 0;
}
這道題其實我wa了近10次,原因就是Move和MoveBack寫錯了,沒有移動nTimes次,而前面一直寫成了1,昨晚wa得實在無語了...今天晚上檢查才突然發現的...
這半個多月做了60道題了,都沒有改動這低級的bug習慣...實在無語...遞歸,回溯,剪枝都寫上了...唉...實在無語...還不如直接9重循環,多省心...真不該歧視某種方法的...
鏈接：
http://poj.grids.cn/practice/1183/
方法1:
本題很容易推斷出,a = (b*c-1)/(b+c), 由于需要求(b+c)的最小值,根據高中的函數思想,如果(b+c)能夠轉換為關于b或者c的函數就好辦了,剛好這里已經有個b和c的關系式子了,可以推導出(b+c) = (c^2+1)/(c-a),這個時候只需要求f(c)的最小值,但是c必須取整數,對這個函數可以求導,也可以進行變形,變形后可以得到f(c) = (c-a)
+ 2*a + (a^2+1)/(c-a),令x=c-a,那么可以得到(b+c)=f(x)=x+2*a+(a^2+1)/x, 其中x必須是整數,到現在為止就是一個用程序模擬高中時候學過的雙曲線函數的求最值問題了,我們知道該函數的極值點是sqrt(a^2+1),但是由于x必須是整數,我們必須從極值開始往下和往上找到一個最小值,然后取2者中的最小值...
這樣這個題就解出來了...
代碼:
#include <stdio.h>
#include <iostream>
#include <math.h>
//b + c = (c^2 + 1) / (c - a) = (c-a) + (2 * a) + (a^2 + 1) / (c -a)
//令c-a = t, f(t) = t + 2*a + (a^2+1)/ t
//因為f(t)在sqrt(a^2+1)時取最小值,但是由于t只能取整數,
//所以,必須從極值點往下和往上尋找最小的值,然后取2者中最小的
int main()
{
long long a;
while (std::cin >> a)
{
long long nTemp = a * a + 1;
long long nDown = sqrt(nTemp);
long long nUp = nDown;
long long one, two;
while (nTemp % nDown )
{
nDown--;
}
one = 2 * a + nTemp / nDown + nDown;
while (nTemp % nUp )
{
nUp++;
}
two = 2 * a + nTemp / nUp + nUp;
std::cout << (one < two ? one : two) << std::endl;
}
return 0;
}
方法2:
#include <stdio.h>
#include <iostream>
#include <math.h>
//a = (b*c-1)/(b+c)
//令b = a + m, c = a + n, c >= b
//-> a*(2*a+m+n) = (a+m)*(a+n)-1
//m*n = a^2 + 1 (n>=m)
//所以,求出a^2+1所有因子對,取其中m+n最小的即可
int main()
{
long long a;
while (std::cin >> a)
{
long long m, n;
long long nTemp = a * a + 1;
long long nMax = sqrt(nTemp);
long long nRes = 1 + nTemp;
for (m = 2; m <= nMax; ++m)
{
if (nTemp % m == 0)
{
n = nTemp / m;
if (m + n < nRes)
{
nRes = m + n;
}
}
}
std::cout << 2 * a + nRes << std::endl;
}
return 0;
}
鏈接:
http://poj.grids.cn/practice/2797/
這題乍看之下確實沒什么思路,后面終于明白題意了,然后突然想到可以用字典樹做,速度當然會是非常快的...
但是其實還有一種更簡單的方法,那就是對所有字符串排序之后,每個字符串的前綴長度其實就是由其前一個和后一個字符串共同決定,
nLen = max(nOne, nTwo), nOne 和 nTwo就分別代表當前字符串和前后字符串公告部分的長度+1后的值...
代碼寫出來寫非常簡單...同學這樣實現了下,也輕松過了...
然后我就辛苦的寫了一棵字典樹...可能我的寫法不是很標準,因為我沒參考什么模板,自己硬想出來怎么寫的...
我的想法是開一個靜態大數組,第一個結點作為根,不存儲數據,從第二個結點開始作為自由空間分配...
其實,就是對26顆字典樹虛擬了個無數據的根結點...
使用了虛擬的根結點后,代碼比用26個根結點簡潔很多...
剛開始我就假設1-26號結點分別為a-z,作為26顆樹的根,
而且下26個結點的位置我用的是索引,沒用指針,后面換成了指針,代碼看起來更舒服了...
#include <stdio.h>
#include <string.h>
#define LETTER_NUM 26
#define WORD_LEN_MAX 25
#define WORD_NUM_MAX 1030
#define NODE_MAX (WORD_LEN_MAX * WORD_NUM_MAX + 10)
struct WORD_TREE
{
char ch;
WORD_TREE* next[LETTER_NUM];
int nTime;
};
WORD_TREE tree[NODE_MAX];
WORD_TREE* pFreeNode = tree + 1;//第一個結點作為頭結點,不存儲數據
char szWords[WORD_NUM_MAX][WORD_LEN_MAX];
void AddToTree(char* pszStr)
{
WORD_TREE* pTree = tree;
while (*pszStr && pTree->next[*pszStr - 'a'])
{
pTree = pTree->next[*pszStr - 'a'];
pTree->nTime++;
++pszStr;
}
while (*pszStr)
{
pFreeNode->ch = *pszStr;
pFreeNode->nTime++;
pTree->next[*pszStr - 'a'] = pFreeNode;
pTree = pFreeNode;
++pszStr;
++pFreeNode;
}
}
int FindPrefix(char* pszStr)
{
WORD_TREE* pTree = tree;
int nLen = 0;
while (*pszStr)
{
++nLen;
pTree = pTree->next[*pszStr - 'a'];
if (pTree->nTime <= 1)
{
break;
}
++pszStr;
}
return nLen;
}
int main()
{
int nCount = 0;
while (scanf("%s", szWords[nCount]) != EOF)
{
AddToTree(szWords[nCount]);
nCount++;
}
for (int i = 0; i < nCount; ++i)
{
int nLen = FindPrefix(szWords[i]);
printf("%s ", szWords[i]);
for (int j = 0; j < nLen; ++j)
{
putchar(szWords[i][j]);
}
putchar('\n');
}
return 0;
}
鏈接：
http://acm.csu.edu.cn/OnlineJudge/problem.php?id=1207
問題描述是：給定一個大于0的整數
N(1<=N<=10^8),判斷其是否可能是一個直角三角形的直角邊(這個三角形的三條邊必須都是整數)...
這個題還是做得我挺郁悶的。。。剛開始完全沒思路。。。后面沒辦法，硬著頭皮往下想，對于勾股定理a^2 + b^2 = c^2,假設N是a,
可以得到a^2 = (c + b) * (c -b), 那么(c+b)和(c-b)是a^2的2個因子,而且(c+b)>=a,(c-b)<=a。。。
到這一步已經可以用程序輕松解決出來了,但是對于任意一個整數N來說,其復雜度都是O(N),那么計算量還是很大的...
這個時候只需要枚舉1-N,求出a^2的2個因子,然后求c和b,如果能得出c和b都是正整數那么,就滿足條件了...
但是這樣還是過不了題,因為數據量不會這么小...數據量好像有
10000組。。。
那么還需要推導出進一步的結論...
因為1和a^2一定是a^2的一對因子,那么(c+b) = a^2和(c-b) = 1一定可以成功,
則可以推導出,2*c = a^2 + 1;
要c可解,a必須為奇數,那么可以推導出如果a是奇數,一定是直角邊了。。。
如果a是偶數了,可以化簡為4*(a/2)^2 = 4*（c+b)*(c-b) = (2c+2b)*(2c-2b) = a^2,那么繼續推導也可以得到一樣的結果了...
結論就是:對于大于等于3的正整數都可以是一條直角邊(>=3也可以根據上面的c和b是正整數推導出來)...
鏈接:
http://poj.grids.cn/practice/2820
鏈接:
http://poj.grids.cn/practice/2801
為啥把這2個不相干的題目放在一起了...說實話這其實也是二個容易的題目,尤其第二個更容易想到...第一個也許暫時
沒那么容易想出來。。。
而且感覺第一個古代密碼還挺有意思的...判斷一個字符串是否能夠通過移位和替換方法加密成另外一個字符串。。。
至于第二個,各位去看看題目吧。。。
也是個解法跟題目不大相關的題目。。。
這2個題最大的特點和共同點就是解法和題目意思想去甚遠。。。
所以我覺得做這種二丈和尚摸不早頭腦的題,思維應該往跟題意背離的方向思考。。。
尤其第一個題，如果只看代碼,即使代碼可讀性再好，也不知道代碼有何意義，有何目的，跟題意有啥關系。。。
不過第一個居然輕松AC了,雖然我2b得搞了個ce和re出來了...
第一個的轉換方法是,計算出現的字符'A'-'Z'的出現次數,然后從大小排序,如果針對加密后的字符串得到的結果一直大于等于
加密前的字符串得到的結果,表明答案是YES...具體還是看代碼吧...
#include <stdio.h>
#include <
string.h>
#include <algorithm>
using std::sort;
bool Greater(
int one,
int two)
{
return one > two;
}
int main()
{
char szOne[110];
char szTwo[110];
int nNumOne[26];
int nNumTwo[26];
while (scanf("%s%s", szOne, szTwo) == 2)
{
memset(nNumOne, 0,
sizeof(
int) * 26);
memset(nNumTwo, 0,
sizeof(
int) * 26);
char* psz = szOne;
while (*psz)
{
++nNumOne[*psz - 'A'];
++psz;
}
psz = szTwo;
while (*psz)
{
++nNumTwo[*psz - 'A'];
++psz;
}
sort(nNumOne, nNumOne + 26, Greater);
sort(nNumTwo, nNumTwo + 26, Greater);
bool bIsYes =
true;
for (
int i = 0; i < 26; ++i)
{
if (nNumOne[i] < nNumTwo[i])
{
bIsYes =
false;
break;
}
}
if (bIsYes)
{
printf("YES\n");
}
else {
printf("NO\n");
}
}
return 0;
}
鏈接:
http://poj.grids.cn/practice/2804/
這也是一個很簡單的題目,大家一看都知道用什么方法了,當然如果是查找的話,順序查找是不行的,
方法一,是用map,建立個map<string, string>的字典,注意不要想當然用map<char*, char*>,
那樣得動態分配內存,或者還是先開個大數組存好字典,其結果還是多浪費了內存...
排序+二分也不錯的,因為數據量確實很大,而且題目也建議用c的io輸入,所以這樣再建立map<string, string>
中間還得轉換一下...
總之做這個題還是很順利的,就wa了一次,原因是2分寫錯了,我也很久沒在oj上寫2分了...
代碼如下:
#include <stdio.h>
#include <
string.h>
#include <algorithm>
#define MAX_WORD_LEN 11
#define MAX_DICTION_ITEM (100000 + 10)
using std::sort;
struct Dictionary
{
char szWord[MAX_WORD_LEN];
char szEnglish[MAX_WORD_LEN];
};
Dictionary diction[MAX_DICTION_ITEM];
bool CmpDictionItem(Dictionary one, Dictionary two)
{
return strcmp(one.szWord, two.szWord) < 0;
}
int FindEnglish(
char* pszWord,
int nItemNum)
{
int nBeg = 0, nEnd = nItemNum - 1;
int nCmp = 0;
while (nBeg <= nEnd)
{
int nMid = (nBeg + nEnd) / 2;
nCmp = strcmp(pszWord, diction[nMid].szWord);
if (nCmp == 0)
{
return nMid;
}
else if (nCmp < 0)
{
nEnd = nMid - 1;
}
else {
nBeg = nMid + 1;
}
}
return -1;
}
int main()
{
char szStr[30];
char szWord[MAX_WORD_LEN];
int nCount = 0;
int nAnsItem = 0;
while (fgets(szStr, 29, stdin), szStr[0] != '\n')
{
sscanf(szStr, "%s%s", diction[nCount].szEnglish, diction[nCount].szWord);
++nCount;
}
sort(diction, diction + nCount, CmpDictionItem);
while (scanf("%s", szWord) == 1)
{
if ((nAnsItem = FindEnglish(szWord, nCount)) != -1)
{
printf("%s\n", diction[nAnsItem].szEnglish);
}
else {
printf("eh\n");
}
}
return 0;
}
其實我的主要目的是為了指出二分的寫法,大家看我的FindEnglish函數,傳遞的是數組的地址和數組的長度,
然后我寫函數體的時候用的是[]的形式,就是下確界,上確界,這樣最重要的是需要考慮循環的條件是<還是
<=,其實這也很好判斷,因為上界和下界都能夠取到,所以=是成立的...而且修改right的時候,必須將right = mid - 1,
原因也是因為這是上確界,
但是如果是上不確界了,那么等號就必須去掉,而且right也只能修改為mid,因為mid-1就是確界了,而mid才是上不確界...
想到這個程度的話,以后寫只有唯一解二分就應該不會出錯了...但是寫查找滿足條件的最大或者最小解的二分還需要其它技巧...
鏈接:
http://poj.grids.cn/practice/2964/
這本來就是一個簡單的題目,但是還是值得我用一篇文章的位置。大家都做過閏年的題目,這只是閏年的一個升級版。。。本來我不至于這么糾結這個題目的,一看到題目,
我就考慮到了一次次減去天數來加年數和月份,而且我還想在讀入數據之前初始化一個存儲2000-9999年每年有多少天得數組...這樣就可以避免循環時候計算每年的天數了...但是我還是怕時間不夠,所以我想到了個O(1)的算法...
那就是按照題目的說明,其實每400是一個周期的,但是我前面寫代碼的時候把4年當中一個小周期,100年當中一個中周期,400年當中一個大周期,同樣的處理了...
事實上,只能對400作為周期處理,其它的必須分類討論,雖然代碼寫出來很復雜,而且我也因為出現這個bug錯了無數次,但是我還是感覺非常值得的...因為這是我獨立思考的成果,耗費了多少時間和精力倒是無所謂...寫算法題,目的不僅僅應該是學習了多少個算法,而是在于能力的提高,個人的嚴謹性,思考問題的完整性等等...一直覺得自己思考問題時候有創意,但是完整性和嚴謹性很低...
下面貼我的代碼吧,只用了10ms,如果采用第一種方法則需要60ms-70ms...
#include <stdio.h>
#define SMALL (365 * 3 + 366)
#define MID (SMALL * 25 - 1)
#define BIG (MID * 4 + 1)
char* pszWeekdays[7] =
{
"Saturday", "Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday"
};
int nDaysOfMon[2][13] =
{
{0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31},
{0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}
};
void GetMonthAndDay(int nDays, bool bIsLeap, int* nMon, int* nDay)
{
int nChoose = 0;
int i = 0;
if (bIsLeap)
{
nChoose = 1;
}
*nMon = *nDay = 0;
i = 1;
while (nDays > nDaysOfMon[nChoose][i])
{
nDays -= nDaysOfMon[nChoose][i];
++i;
}
*nMon = i;
*nDay = nDays;
}
void CountSmall(int* pnDays, int* pnPastYears, int* pnMon, int* pnDay)
{
if (*pnDays >= 3 * 365)//4
{
*pnPastYears += 3;
*pnDays -= 365 * 3;
GetMonthAndDay(*pnDays + 1, true, pnMon, pnDay);
}
else//1-3
{
*pnPastYears += *pnDays / 365;
*pnDays %= 365;
GetMonthAndDay(*pnDays + 1, false, pnMon, pnDay);
}
}
int main()
{
int nPastDays = 0;
int nPastYears = 0;
int nYear = 0, nMon = 0, nDay = 0;
while (scanf("%d", &nPastDays), nPastDays != -1)
{
int nTemp = nPastDays;
nPastYears = 0;
if (nTemp < 366)
{
GetMonthAndDay(nTemp + 1, true, &nMon, &nDay);
nPastYears = 0;
}
else
{
nPastYears++;
nTemp -= 366;
nPastYears += (nTemp / BIG) * 400;
nTemp %= BIG;
if (nTemp >= MID * 3)//301-400年(以4為周期)
{
nTemp -= MID * 3;
nPastYears += 300;
nPastYears += nTemp / SMALL * 4;
nTemp %= SMALL;
CountSmall(&nTemp, &nPastYears, &nMon, &nDay);
}
else//1-300年
{
nPastYears += nTemp / MID * 100;
nTemp %= MID;
if (nTemp >= SMALL * 24)//97-100年(4個平年)
{
nTemp -= SMALL * 24;
nPastYears += 4 * 24;
nPastYears += nTemp / 365;
nTemp %= 365;
GetMonthAndDay(nTemp + 1, false, &nMon, &nDay);
}
else//1-96年
{
nPastYears += nTemp / SMALL * 4;
nTemp %= SMALL;
CountSmall(&nTemp, &nPastYears, &nMon, &nDay);
}
}
}
printf("%d-%02d-%02d %s\n", nPastYears + 2000, nMon, nDay, pszWeekdays[nPastDays % 7]);
}
return 0;
}