題目意思很簡單就是計算含括號的四則運算表達式的值。這個題目很坑爹，剛做的時候，題目描述里面只說里面會有空格，
后面居然把題目描述改了。所以，這個題無論怎么改，都是不對。因為，不知道是哪個坑爹的出題人，把數據里面加了\t，
難道出題人以為\t也是空格。估計，后面修改題目描述，也是發現這個問題后才改的。這可是還是哥了，改了無數多遍，
不處理非法數據就超時，略過非常數據當然直接WA了。好坑爹。
計算表達式的值，以前嚴蔚敏書上就說用棧構造出來后綴表達式后再計算值。但是這個方法未免太那個了，首先太麻煩了，
雖然算法思路不麻煩。我的做法是直接遞歸計算即可。碰到左括號遞歸計算新的表達式，
右括號作為函數終止條件。否則，按照
四則運算的優先級計算當前的表達式。遞歸算法中需要記錄前一個運算符合的優先級，
如果前一個運算符的優先級比現在碰到的
運算符的優先級高，那么就應該直接返回答案了，當前碰到的運算符的計算交給下一次循環好了。
代碼如下：
#include <stdio.h>
#define MAX (100 + 10)
char szData[MAX];
void TrimSpace(char* pszData)
{
char* pszRead = pszData;
char* pszWrite = pszData;
while (*pszRead)
{
//由于數據中有\t,與先前題目描述不符合,不處理掉就直接超時了
if (*pszRead != ' ' && *pszRead != '\t')
{
*pszWrite++ = *pszRead;
}
++pszRead;
}
*pszWrite = '\0';
}
//nKind代表前一個運算符合的優先級,開始時是0,+-是1,*/是2
double Cal(char*& pszData, int nKind)
{
double fAns = 0.0;
while (*pszData && *pszData != ')')//表達式終止的條件是到達'\0'或者碰到右括號
{
if (*pszData >= '0' && *pszData <= '9')
{
fAns = 10 * fAns + *pszData - '0';
++pszData;
}
else if (*pszData == '+')
{
if (nKind >= 1)
{
return fAns;
}
++pszData;
fAns += Cal(pszData, 1);
}
else if (*pszData == '-')
{
if (nKind >= 1)
{
return fAns;
}
++pszData;
fAns -= Cal(pszData, 1);
}
else if (*pszData == '*')
{
if (nKind >= 2)
{
return fAns;
}
++pszData;
fAns *= Cal(pszData, 2);
}
else if (*pszData == '/')
{
if (nKind >= 2)
{
return fAns;
}
++pszData;
fAns /= Cal(pszData, 2);
}
else if (*pszData == '(')
{
++pszData;
fAns = Cal(pszData, 0);
++pszData;//移到')'后面
return fAns;//一個括號內的是一個完整的表達式,因此直接返回
}
}
return fAns;
}
int main()
{
while (gets(szData))
{
TrimSpace(szData);
char* pszData = szData;
printf("%.4f\n", Cal(pszData, 0));
}
}
一個遞歸函數能計算出表達式的值，而且能處理優先級和括號，如果是以前的話，我應該是寫不出來的。再把算法的實現細節改改，
應該也能計算出浮點數的表達式了。
這是個簡單的字符串處理題目。看題目，數據應該不是很大，直接暴力處理可以過。如果為了加快搜索速度，在中間輸入過程中排序，
再二分很麻煩，速度也快不了多少，因為只是輸入的過程中需要查找。但是，這個題其實很好用map做，代碼量可以少很多，也很簡潔。
寫這篇blog的目的是為了提醒自己，容易題再這樣錯下去，真的很傷人心，學什么都沒必要了，當時打算繼續搞ACM的目的之一就是
為了提高代碼正確率。這個題，不僅細節部分沒看清楚，而且寫代碼時候把比較函數里面的one.nLost寫成了one.nGet，查錯了1個多
小時，還讓隊友幫忙查錯了好久，真的很無語。寫程序確實可以debug，但是這也讓我養成了很嚴重的依賴debug的習慣。
人生不可以debug，人生不可以重來。記得以前很多次很多事情就是開始無所謂，后面悲催到底，無限后悔。
代碼如下：
1 #include <stdio.h> 2 #include <
string.h>
3 #include <
string>
4 #include <map>
5 #include <vector>
6 #include <algorithm>
7 #define MAX (100)
8 using std::map;
9 using std::
string;
10 using std::vector;
11 using std::sort;
12 13 struct INFO
14 {
15 INFO()
16 {
17 nScore = nGet = nLost = 0;
18 }
19 20 string strName;
21 int nScore;
22 int nGet;
23 int nLost;
24 bool operator < (
const INFO& one)
const 25 {
26 if (nScore != one.nScore)
27 {
28 return nScore > one.nScore;
29 }
30 else if (nGet - nLost != one.nGet - one.nLost)
//這里把one.nLost寫成了one.nGet
31 {
32 return nGet - nLost > one.nGet - one.nLost;
33 }
34 else if (nGet != one.nGet)
35 {
36 return nGet > one.nGet;
37 }
38 else 39 {
40 return strName < one.strName;
41 }
42 }
43 };
44 45 int main()
46 {
47 int nN;
48 49 //freopen("in.txt", "r", stdin);
50 //freopen("out.txt", "w", stdout);
51 while (scanf("%d", &nN) == 1)
52 {
53 int nLast = nN * (nN - 1);
54 char szOne[MAX];
55 char szTwo[MAX];
56 int nOne, nTwo;
57 58 map<
string, INFO> myMap;
59 for (
int i = 0; i < nLast; ++i)
60 {
61 scanf("%s %*s %s %d:%d", szOne, szTwo, &nOne, &nTwo);
62 //printf("%s %s %d %d\n", szOne, szTwo, nOne, nTwo);
63 64 string strOne = szOne;
65 myMap[strOne].strName = strOne;
66 myMap[strOne].nGet += nOne;
67 myMap[strOne].nLost += nTwo;
68 69 string strTwo = szTwo;
70 myMap[strTwo].strName = strTwo;
71 myMap[strTwo].nGet += nTwo;
72 myMap[strTwo].nLost += nOne;
73 74 if (nOne > nTwo)
75 {
76 myMap[strOne].nScore += 3;
77 }
78 else if (nOne == nTwo)
79 {
80 myMap[strOne].nScore += 1;
81 myMap[strTwo].nScore += 1;
82 }
83 else 84 {
85 myMap[strTwo].nScore += 3;
86 }
87 }
88 89 map<
string, INFO>::iterator it;
90 vector<INFO> myVt;
91 for (it = myMap.begin(); it != myMap.end(); it++)
92 {
93 myVt.push_back(it->second);
94 }
95 96 sort(myVt.begin(), myVt.end());
97 for (
int i = 0; i < myVt.size(); ++i)
98 {
99 printf("%s %d\n", myVt[i].strName.c_str(), myVt[i].nScore);
100 }
101 printf("\n");
102 }
103 104 return 0;
105 }
兩個棧實現一個隊列
要求：只能使用棧的pop和push，以及測試棧是否為空三個操作。
實現思路：
隊列里面使用stack one 和 stack two。
進隊列時，直接進入棧one即可。
出隊列時，從two彈出一個元素，如果two里面的元素為空，則將one里面的元素依次彈出并壓入two中，再從two彈出一個元素返回。
用STL里面的stack模擬實現queue的代碼如下：
1 #include <stdio.h> 2 #include <stdlib.h>
3 #include <time.h>
4 #include <stack>
5 using std::stack;
6
7 template<class T> class CQueue
8 {
9 public:
10 CQueue()
11 {
12 nSize = 0;
13 }
14
15 void clear()
16 {
17 while (!one.empty())
18 {
19 one.pop();
20 }
21 while (!two.empty())
22 {
23 two.pop();
24 }
25 }
26
27 void push(const T& t)
28 {
29 one.push(t);
30 ++nSize;
31 }
32
33 void pop()
34 {
35 if (two.empty())
36 {
37 while (!one.empty())
38 {
39 two.push(one.top());
40 one.pop();
41 }
42 }
43 two.pop();
44 --nSize;
45 }
46
47 T& front()
48 {
49 if (two.empty())
50 {
51 while (!one.empty())
52 {
53 two.push(one.top());
54 one.pop();
55 }
56 }
57 return two.top();
58 }
59
60 T& back()
61 {
62 return one.top();
63 }
64
65 bool empty()
66 {
67 return nSize == 0;
68 }
69
70 private:
71 stack<T> one;
72 stack<T> two;
73 int nSize;
74 };
75
76 #define MAX 20
77
78 int main()
79 {
80 CQueue<int> q;
81
82 srand(time(NULL));
83 for (int i = 0; i < MAX; ++i)
84 {
85 q.push(i);
86
87 if (rand() % 2)
88 {
89 printf("front: %d\n", q.front());
90 q.pop();
91 }
92 }
93
94 while (!q.empty())
95 {
96 printf("front: %d\n", q.front());
97 q.pop();
98 }
99
100 return 0;
101 }
102
兩個隊列實現一個棧
要求：只能使用從隊列的尾部入和頭部出，以及測試隊列是否為空三個操作。
實現思路：
隊列里面使用queue one 和 stack two。
進棧時，根據當前元素是全部存儲在哪個隊列而選擇從one或者two的尾部進入。
出棧時，假設當前元素都存儲在one里面，則不斷出隊列，直到隊列為空之前的所有元素一次進入隊列two，而one里面的最后一個元素
作為棧彈出的值返回。
對于當前元素是存儲在哪個隊列里面，可以設置變量標記，初始化時候存儲在one里面，操作一次，由于元素要倒轉，則存儲位置會變
一次。
用STL里面的queue模擬實現的stack代碼如下：
1 #include <stdio.h> 2 #include <queue>
3 using std::queue;
4
5 template<class T> class CStack
6 {
7 public:
8 CStack()
9 {
10 nSize = 0;
11 nTime = 1;
12 }
13
14 void clear()
15 {
16 while (!one.empty())
17 {
18 one.pop();
19 }
20 while (!two.empty())
21 {
22 two.pop();
23 }
24 }
25
26 void push(const T& t)
27 {
28 if (nTime % 2)
29 {
30 one.push(t);
31 }
32 else
33 {
34 two.push(t);
35 }
36 ++nSize;
37 }
38
39 void pop()
40 {
41 if (nTime % 2)
42 {
43 while (!one.empty())
44 {
45 T t = one.front();
46 one.pop();
47 if (!one.empty())
48 {
49 two.push(t);
50 }
51 }
52 }
53 else
54 {
55 while (!two.empty())
56 {
57 T t = two.front();
58 two.pop();
59 if (!two.empty())
60 {
61 one.push(t);
62 }
63 }
64 }
65
66 nTime = (nTime + 1) % 2;
67 --nSize;
68 }
69
70 T& top()
71 {
72 if (nTime % 2)
73 {
74 while (!one.empty())
75 {
76 T t = one.front();
77 one.pop();
78 if (!one.empty())
79 {
80 two.push(t);
81 }
82 else
83 {
84 two.push(t);
85 nTime = (nTime + 1) % 2;
86 return two.back();
87 }
88 }
89 }
90 else
91 {
92 while (!two.empty())
93 {
94 T t = two.front();
95 two.pop();
96 if (!two.empty())
97 {
98 one.push(t);
99 }
100 else
101 {
102 one.push(t);
103 nTime = (nTime + 1) % 2;
104 return one.back();
105 }
106 }
107 }
108 }
109
110 bool empty()
111 {
112 return nSize == 0;
113 }
114
115 private:
116 queue<T> one;
117 queue<T> two;
118 int nSize;
119 int nTime;
120 };
121
122 #define MAX 20
123
124 int main()
125 {
126 CStack<int> stack;
127
128 for (int i = 0; i < MAX; ++i)
129 {
130 stack.push(i);
131 }
132
133 while (!stack.empty())
134 {
135 printf("top: %d\n", stack.top());
136 stack.pop();
137 }
138
139 return 0;
140 }
141
帶權中位數定義如下：
郵局位置問題定義如下：
上一篇文章輸油管道問題里面證明了，當權值Wi都為1的時候，中位數就是最佳的解。但是，現在Wi已經不一定是1了。所以，現在
需要證明在任意Wi的取值情況下，帶權中位數能夠成為郵局位置的最佳解。假設，所有Wi都是1的倍數，如果是小數的話，可以所有的
Wi都乘以一定的倍數。那么wi*d(p,pi) =
Σ(p,pi)(i從1到wi)，這個意思是把距離乘以了wi倍。
但是，現在可以換一種看法，換成了pi位置有wi個重合的點，且每一個點的權值都是1，那么其和也是wi*d(p,pi)。那么對所有的pi
都這樣分解，就把問題重新轉換成了輸油管道問題了。輸油管道問題的最優解就是中位數，那么郵局問題的最優解就是轉換之后的
這些點的中位數點。而這個點一定存在于帶權中位數那個點分解出的一堆點中。
二維郵局問題的解法是把x和y分開求2次一維郵局問題，然后把解組和起來，得到答案。
求帶權中位數的算法比較簡單，直接的做法是，先把n個點按照位置排序，然后按點的位置從小到大遍歷，找到滿足要求的點即可。
不算排序點位置的預處理，因為很多時候點應該就是按順序給出的，所以其時間復雜度是O(n)。
要求：
先看算導上輸油管道問題的描述：
這個題，雖然說給出了井的x,y坐標，但是要修建的主管道卻只是一條橫向的，而且其余管道也只是到這條管道的豎向距離。
那么，就轉換為確定一條直線 y = m，使得其它個點到這條直線的距離最多。也許不需要多的提示，大家的直覺就會想到應該
選所有y值的中點。但是，這個的證明卻不是那么的明顯。
證明如下：
設所有的y值系列為y1,y2,...,yn，并且假設這個是按遞增排列的。我們要求的是Sum =
Σ|yi-m|(1<=i<=n),
1）顯然假如選小于y1或者大于yn的y=m都不會比選y1或者yn更好。
2）如果選y1或者yn，那么|y1-m|+|yn-m| = |yn-y1|都是一樣的結果，甚至選y1和yn之間的任意一個值。
3）如此繼續下去，對于y2和yn，也有2）所描述的性質
4）繼續到最后，只需要取最中間一對點之間的值即可，如果n是奇數，那么就是中間的點，如果n是偶數，取任意一個中間
點都可以。
通過上面證明，我們可以選取第y(n/2 + 1)作為修建主管道的地方。當然這可能是唯一的最優選擇，或者無數個最優選擇中的一個。
那么現在已經轉換為求中位數了，求中位數的辦法最簡單的是對序列排序然后取中間的即可。算法導論上有一種平均代價
O(n)的辦法，
思路類似于快速排序，快排的每一次操作都是劃分數組，前小后大，如果我們也這一次次去劃分數組，剛好軸元素處于我們要求的那個位置
上那么就達到我們的目的了，下面的代碼中
Select函數就是求一個數組的中位數。
對于POJ 1723題，很顯然y的選擇是中位數即可，x的選擇需要轉換一下也變成求中位數了。題目中描述，最后要達到的效果是每個士
兵都占成一橫排，而且彼此相鄰，也就是y相同，但是x系列是k,k+1,k+2,...,k+n-1。那么如何從原來的x0,x1,x2,...,x(n-1)移動過去了。
可以簡單的考慮下，
將最左邊的士兵移動到k,次左的移動到k+1,...,最右邊的移動到k+n-1，所需要的移動之和一定是最小的。那么我們
可以將原來的x0-x(n-1)排序，得到x'0,x'1,...,x'(n-1),要求的
Sum = Σ|x'i - (k + i)| = Σ|(x'i - i) - k|,那么要使Sum最小，只需要
求序列X'i - i的中位數即可了。
代碼如下：
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
using std::sort;
using std::swap;
#define MAX (10000 + 10)
int Partion(int* pnA, int nLen)
{
int i, j;
for (i = j = 0; i < nLen - 1; ++i)
{
if (pnA[i] < pnA[nLen - 1])
{
swap(pnA[i], pnA[j++]);
}
}
swap(pnA[j], pnA[nLen - 1]);
return j;
}
int Select(int* pnA, int nLen, int nIndex)
{
if (nLen > 1)
{
int nP = Partion(pnA, nLen);
if (nP + 1 == nIndex)
{
return pnA[nP];
}
else if (nP + 1 > nIndex)
{
return Select(pnA, nP, nIndex);
}
else
{
return Select(pnA + nP + 1, nLen - nP - 1, nIndex - nP - 1);
}
}
else
{
return pnA[0];
}
}
int main()
{
int nX[MAX];
int nY[MAX];
int nN;
int i;
while (scanf("%d", &nN) == 1)
{
for (i = 0; i < nN; ++i)
{
scanf("%d%d", &nX[i], &nY[i]);
}
int nMY = Select(nY, nN, nN / 2 + 1);
sort(nX, nX + nN);
for (i = 0; i < nN; ++i)
{
nX[i] = nX[i] - i;
}
int nMX = Select(nX, nN, nN / 2 + 1);
int nSum = 0;
for (i = 0; i < nN; ++i)
{
nSum += abs(nX[i] - nMX);
nSum += abs(nY[i] - nMY);
}
printf("%d\n", nSum);
}
return 0;
}
雖然簡易二字，因人而異。不過，寫一個快排確實并不需要過20行，超過幾分鐘時間的代碼。面試的時候，面試官確實會經常問起快排什么的。但是，大家上的入門課基本是使用嚴蔚敏老奶奶的教材，上面對于快排的講解我是不敢恭維的。至少上面關于快排的寫法，我是寫過好幾次之后都是沒掌握好的。后面，應該是看K&R的c語言程序設計時候，發現一種更簡便的partion方法，但是當時我也沒怎么掌握。這一切直到，寒假認真閱讀算法導論的時候。
不用算法牛人，算法學得好或者對快排理解深刻的，不用把這篇文章看完了，相信你們都能在10分鐘之內寫一個正確的快排了。
廢話少說，還是來講講如何保證10分鐘之內寫一個正確的快排，而且以后都能10分鐘之內寫出來，而不是此刻看了我說的這些胡言之后。
快排的主函數大家都會，現在我給個簡易點的樣子：
void QuickSort(int* pnA, int nLen)
{
if (nLen > 1)
{
int nP = Partion(pnA, nLen);
QuickSort(pnA, nP);//排序第nP+1個元素前面的nP個元素
QuickSort(pnA + nP + 1, nLen - nP - 1);//排序第nP+1個元素后面的元素
}
}
那么現在就剩下Partion函數了。
我記得嚴蔚敏書上的寫法中Partion 函數里面是有幾個循環的。而且即使大概寫出來了，也很難處理正確邊界。
現在，我要說的就是算法導論上，作為教材內容出現的Partion函數。還是看代碼吧。
int Partion(int* pnA, int nLen)
{
//這里選擇最后一個元素作為軸元素
int i, j;
for (i = j = 0; i < nLen - 1; ++i)
{
if (pnA[i] < pnA[nLen - 1])
{
swap(pnA[i], pnA[j];//交換2個數的函數，大家都能寫吧，stl中也有
++j;
}
}
swap(pnA[j], pnA[nLen - 1]);
return j;
}
為了公平起見，上面的代碼我都是在blog上面直接敲的，寫這10多行代碼是絕對用不了10分鐘的。主遞歸函數大家都會寫，Partion函數里面只有一個for循環，所以只要明確了for循環的意思，快排的速寫就迎刃而解了。其實，按照算導的說法，
這個for一直在劃分區間。區間[0,j-1]是小于最后一個元素的區間，[j,nLen - 2]是大于等于最后一個元素的區間，所以最后將第nLen-1個元素與第j個元素交換即可，Partion應該返回的值也應該是j。
我不知道大家理解上面那句黑體字的話沒，如果理解了，隨便寫個快排是沒問題了。至少，可能的下次面試時候，可以瀟灑地寫個快排給面試官看看了，雖然這也許并不是什么值得慶幸的事情。
算法導論里面的快速排序那章后面還有思考題，其中第一個思考題，提出的另外一種叫做Hoare劃分的partion寫法，意思就和嚴蔚敏書上的partion函數一致的。理解的關鍵是，
軸元素一直處于被交換中。只要發現了這點，寫一兩次后，這種partion方法也能掌握好了，不過寫起來是循環嵌循環了，沒那么舒服。
這個算法的應用，比如洗牌，這個大家都非常熟悉。很久以前用的是最原始的方法，就是一直rand()未出現的牌，直至生成所有的牌。
這當然是一個while(1)循環，很爛的算法吧。后面聽說直接交換牌，打亂即可了。但是打亂后生成的排列是隨機的么，是等可能隨機的么。
其實，這個問題上算法導論上早已經有了答案了，看過算法導論之后覺得沒看之前真的是算法修養太差了。
算法的偽代碼如下圖所示：
具體c++實現如下：
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <time.h>
// void Swap(int& nOne, int& nTwo)
// {
// nOne = nOne + nTwo;
// nTwo = nOne - nTwo;
// nOne = nOne - nTwo;
// }
void Swap(int& nOne, int& nTwo)
{
int nTemp;
nTemp = nOne;
nOne = nTwo;
nTwo = nTemp;
}
//返回一個在區間[nBeg, nEnd]內的隨機數
int Random(int nBeg, int nEnd)
{
assert(nEnd >= nBeg);
if (nBeg == nEnd)
{
return nBeg;
}
else
{
return rand() % (nEnd - nBeg + 1) + nBeg;
}
}
void RandomizeInPlace(int* pnA, int nLen)
{
static bool s_bFirst = false;
if (!s_bFirst)
{
srand(time(NULL));
s_bFirst = true;
}
for (int i = 0; i < nLen; ++i)
{
Swap(pnA[i], pnA[Random(i, nLen - 1)]);
}
}
int main()
{
int nArray[20];
int i, j;
for (i = 1; i <= 20; ++i)
{
int nCnt = i;
while (nCnt--)
{
for (j = 0; j < i; ++j)
{
nArray[j] = j;
}
RandomizeInPlace(nArray, i);
for (j = 0; j < i; ++j)
{
printf("%d ", nArray[j]);
}
printf("\n");
}
printf("\n");
}
return 0;
}
運行效果圖片如下：
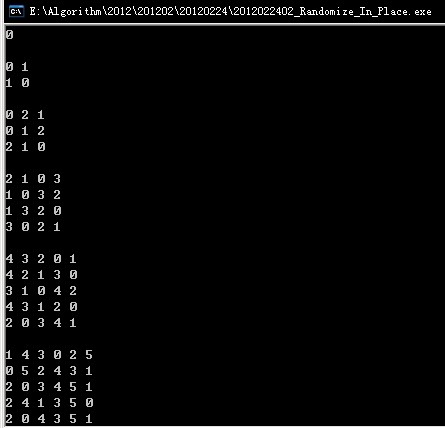
根據運行結果大致就可以感覺到，生成的排列都是隨機的。
這里要多說一句那就是我注釋的那個交換函數其實是有bug的，也許這才是不提倡使用這個交換方法的真正原因，而不僅僅是
難以理解。用同一個變量去調用該函數，會將該變量置0，而不是保持原來的值?。?！
至于如何證明這個算法生成的均勻隨機的排列，可以參考算法導論5.3節最后一部分。
證明的大致思路是利用循環不變式的證明方法：證明i次循環后得到某個排列的概論是(n -i)! / n!，那么n次循環后得到最終那個排列的
概論就是1/n!，這樣就證明了該算法能夠得到均勻隨機排列。
這個算法其實就是隨機化算法的一種，其實快排也有所謂的隨機化版本，改動的地方只是隨機選擇了中軸元素而已，這個
在算法導論上也有介紹。
今天在做課設，由于想給程序加上刪除以前的配置文件的功能，由于某種原因，同類型的文件比較多，加上暑假實習的時候，
做了個用dir命令實現的批量文件修改器，所以決定用del命令，一下子寫好后，發現以前由于沒有要求做界面，而現在課設我用
的是MFC里面的CFormView做的界面，所以會閃爍而過一個console窗口，實在不爽之，所以，找方法去掉它。
網上找來找去，只找到啟動cmd，傳參數的都很少，傳參數時候組合參數的更加少，加上我對dos命令不熟悉，所以實在悲催，
浪費了不少時間。
這種東西，一直竊以為有人做好之后，提供比較合格的接口，大家以后都方便，所以貼出來，大家雅俗共賞，批評下。
還發現網上的代碼有個問題，居然大多把直接cmd路徑寫上去，其實大家都知道，系統路徑是不確定的，所以特定修正了這個bug，
而且我也實驗了下，無論參數是絕對路徑還是相對路徑這個函數都是有效的。
大家用這個函數的時候，記得cmd命令都是可以匹配通配符的哦。
函數代碼如下:
//批量刪除指定格式文件,不顯示console窗口
void BatchDelFile(char* pszFile)
{
char szDelCmd[MAX_INFO_LEN];
char szCurDir[MAX_PATH];
char szCmdPath[MAX_PATH];
SHELLEXECUTEINFO shExecInfo = {0};
GetCurrentDirectory(MAX_PATH, szCurDir);//獲取當前路徑
GetSystemDirectory(szCmdPath, MAX_PATH);//獲取cmd路徑
strcat(szCmdPath, "\\cmd.exe");
sprintf(szDelCmd, "%s /c del /f /q /s %s",
szCmdPath, pszFile);//格式化出命令字符串, 注意加上/c, 還有那2個""
shExecInfo.cbSize = sizeof(SHELLEXECUTEINFO);
shExecInfo.fMask = SEE_MASK_NOCLOSEPROCESS;
shExecInfo.hwnd = NULL;
shExecInfo.lpVerb = NULL;
shExecInfo.lpFile = szCmdPath;//cmd的路徑
shExecInfo.lpParameters = szDelCmd;//程序參數,參數格式必須保證正確
shExecInfo.lpDirectory = szCurDir;//如果szFile是相對路徑,那個這個參數就會起作用
shExecInfo.nShow = SW_HIDE;//隱藏cmd窗口
shExecInfo.hInstApp = NULL;
ShellExecuteEx(&shExecInfo);
WaitForSingleObject(shExecInfo.hProcess, INFINITE);//無限等待cmd窗口執行完畢
}
以下是我在一個消息出來函數的調用：
char szDelFiles[MAX_PATH];
sprintf(szDelFiles, "\"*.tcp.txt\" + \"*.udp.txt\"");
BatchDelFile(szDelFiles);
為了調用方便，我還實現了一個可變參數列表的版本，以及一個傳一個文件名數組的版本。
可變參數版本代碼如下：
//批量刪除指定格式文件,不顯示console窗口
void BatchDelFile(int nNum, ...)
{
va_list argPtr;
int i;
char* pszDelCmd;
char szCurDir[MAX_PATH];
char szCmdPath[MAX_PATH];
SHELLEXECUTEINFO shExecInfo = {0};
pszDelCmd = (char*)malloc((nNum + 2)* MAX_PATH);
GetCurrentDirectory(MAX_PATH, szCurDir);//獲取當前路徑
GetSystemDirectory(szCmdPath, MAX_PATH);//獲取cmd路徑
strcat(szCmdPath, "\\cmd.exe");
sprintf(pszDelCmd, "%s /c del /f /q /s ", szCmdPath);//格式化出命令字符串, 注意加上/c
va_start(argPtr, nNum);
for(i = 0; i < nNum; ++i)
{
strcat(pszDelCmd, "\"");
strcat(pszDelCmd, *(char**)argPtr);
strcat(pszDelCmd, "\"");
if (i != nNum - 1)
{
strcat(pszDelCmd, " + ");
}
va_arg(argPtr, char**);
}
va_end(argPtr);
shExecInfo.cbSize = sizeof(SHELLEXECUTEINFO);
shExecInfo.fMask = SEE_MASK_NOCLOSEPROCESS;
shExecInfo.hwnd = NULL;
shExecInfo.lpVerb = NULL;
shExecInfo.lpFile = szCmdPath;//cmd的路徑
shExecInfo.lpParameters = pszDelCmd;//程序參數,參數格式必須保證正確
shExecInfo.lpDirectory = szCurDir;//如果szFile是相對路徑,那個這個參數就會起作用
shExecInfo.nShow = SW_HIDE;//隱藏cmd窗口
shExecInfo.hInstApp = NULL;
ShellExecuteEx(&shExecInfo);
WaitForSingleObject(shExecInfo.hProcess, INFINITE);//無限等待cmd窗口執行完畢
free(pszDelCmd);
}
調用方法：
BatchDelFile(2, "*.tcp.txt", "*.udp.txt");//第一個是文件個數，后面依次是文件路徑，文件路徑可以是相對路徑也可以是絕對路徑。
文件名數組的版本代碼如下：
void BatchDelFile(int nNum, char** pszFiles)
{
int i;
char* pszDelCmd;
char szCurDir[MAX_PATH];
char szCmdPath[MAX_PATH];
SHELLEXECUTEINFO shExecInfo = {0};
pszDelCmd = (char*)malloc((nNum + 2)* MAX_PATH);
GetCurrentDirectory(MAX_PATH, szCurDir);//獲取當前路徑
GetSystemDirectory(szCmdPath, MAX_PATH);//獲取cmd路徑
strcat(szCmdPath, "\\cmd.exe");
sprintf(pszDelCmd, "%s /c del /f /q /s ", szCmdPath);//格式化出命令字符串, 注意加上/c
for(i = 0; i < nNum; ++i)
{
strcat(pszDelCmd, "\"");
strcat(pszDelCmd, *(pszFiles + i));
strcat(pszDelCmd, "\"");
if (i != nNum - 1)
{
strcat(pszDelCmd, " + ");
}
}
shExecInfo.cbSize = sizeof(SHELLEXECUTEINFO);
shExecInfo.fMask = SEE_MASK_NOCLOSEPROCESS;
shExecInfo.hwnd = NULL;
shExecInfo.lpVerb = NULL;
shExecInfo.lpFile = szCmdPath;//cmd的路徑
shExecInfo.lpParameters = pszDelCmd;//程序參數,參數格式必須保證正確
shExecInfo.lpDirectory = szCurDir;//如果szFile是相對路徑,那個這個參數就會起作用
shExecInfo.nShow = SW_HIDE;//隱藏cmd窗口
shExecInfo.hInstApp = NULL;
ShellExecuteEx(&shExecInfo);
WaitForSingleObject(shExecInfo.hProcess, INFINITE);//無限等待cmd窗口執行完畢
free(pszDelCmd);
}
調用方法：
char* szFiles[2];
szFiles[0] = "*.tcp.txt";
szFiles[1] = "*.udp.txt";
BatchDelFile(2, szFiles);
首先，快點回家過個好年，回家吃好睡好玩好。
第二，明年畢業設計最好一路順風，選的題是個圖像處理的，但是我目前還一無所知，沒辦法，誰叫選的導師是做圖像的了。
第三，明年過了六級或者說能讓六級達到500分，程序員英語太懶確實有點不負責任啊。
第四，也去考個軟考系分什么的吧，盡可能分配的力量考好一點，省的到時候有人認為我基礎課都是打醬油的。
第五，明年暑假再找個地實習吧，希望比西山居的補助高點，以后待學校的日子實在是太窮了。
第六，算法或者說ACM，明年是最后可能的機會去參加正式的比賽，以前一直玩其它的東西，算法比賽一直在渾水摸魚打醬油，
跟認真搞過算法的完全無法比，所以這才是最重要的一件事情，繼續保證前段時間的狀態，唉，最近已經半個月左右沒刷題了。
第七，既然要從信息安全畢業，安全這東西不能太水了，明年深入下安全開發這東西，雖然這幾年醬油的范圍比較廣，但是，
不能太紙上談兵了，妞被別人泡了，再也沒心思瞎想浪費時間了，還是追求哥自己的小小愿望吧。。。
世界末日來臨之前，以上七條還是得盡可能實現些啊，人最可怕的事情是無聊，沒理想沒追求的人其實過得不無聊，有追求又不行動的人，
其實活得最壓抑。。。一直以來活得比較自由散漫，不喜歡的做的事情參與的少，空閑的時間多，但是也因為對自己狠不下心來，錯過了
很多東西。不是希望，而是要求自己，強烈要求自己在2012年完成任務，完成目標，只此要求，完成目標，也是玩成目標，好好玩，
如果自己都不喜歡的事情，還是盡可能不要去做了。
----------------------------------------------------------------------------------------------------------------
3，4，5月計劃：
寫算法代碼，
看算法導論，
學圖像處理等搞定畢設，
繼續背單詞，聽聽力，爭取這學期過了六級，
早起鍛煉身體。
------------------------------------------------------------------------------------------------------------------
話說現在已經10月份了，6級沒過，暑假怎么可能去實習了，肯定得在學校參加acm集訓的。。。怎么這么容易就能泡到妞了。
而且今年一分錢都沒有，好窮。今晚12點就去比賽了，祝愿一路順風吧。。。
題目1描述:
輸入:一個序列s,該序列里面可能會有同樣的字符,不一定有序
輸出:打亂輸入中的序列,可能產生的所有新的序列
題目2描述:
輸入:一個序列s,該序列里面可能會有同樣的字符,不一定有序 和 一個整數k
輸出:該序列往后計算第k個序列,所有序列是以字典序排序的
如果會有序搜索的童鞋自然而然能立刻做出來第一個題目,可是第二個題目在s較長的情況下,卻需要用模擬而不是搜索...
大家都知道STL里面有個泛函模版, prev_permutation和next_permutation,用法也很簡單,實現的就是題目2的功能...
但是算法最好得靠自己想出來,自己想出來的才是自己的,碰到新的問題才能產生思想的火花...
廢話少說,題目1的解法就是深搜,不過需要加上一個bool數組標記和一個函數確定不同字符之間的大小(有可能這個大小還不是Ascii碼就能決定的),
大致描述下搜索過程,比如輸入序列是12345,那么我搜索的過程大致是第一層按順序選取1-5,進入第二層的時候也是按順序選取1-5,
以此類推,但是每一層里面都只能選前面的層次沒有選過的數,而且因為有重復字符,算法還必須保證每一層里面按順序選取的字符必須是升序的,
熟悉順序搜索和回溯的同學,很自然就會產生這樣的想法...
POJ - 1256的代碼如下:
#include <stdio.h>
#include <string.h>
#include <ctype.h>
#include <stdlib.h>
#include <algorithm>
#define MAX (13 + 10)
using namespace std;
bool bUsed[MAX];
char szAns[MAX];
char szInput[MAX];
bool CmpChar(char chOne, char chTwo)
{
if (abs(chOne - chTwo) != 'a' - 'A')
{
return tolower(chOne) - tolower(chTwo) < 0;
}
return chOne - chTwo < 0;
}
bool Greater(char chOne, char chTwo)
{
if (abs(chOne - chTwo) != 'a' - 'A')
{
return tolower(chOne) - tolower(chTwo) > 0;
}
return chOne - chTwo > 0;
}
void Gen(int nDepth, int nLen)
{
if (nDepth == nLen)
{
szAns[nLen] = '\0';
printf("%s\n", szAns);
return;
}
char chLast = '\0';
for (int i = 0; i < nLen; ++i)
{
if (!bUsed[i] && Greater(szInput[i], chLast))
{
bUsed[i] = true;
szAns[nDepth] = szInput[i];
Gen(nDepth + 1, nLen);
bUsed[i] = false;
chLast = szInput[i];
}
}
}
int main()
{
int nCases;
scanf("%d", &nCases);
while (nCases--)
{
scanf("%s", szInput);
int nLen = strlen(szInput);
sort(szInput, szInput + nLen, CmpChar);
Gen(0, nLen);
}
return 0;
}
題目2的解法是模擬,功能類似與STL的那2個泛型模版函數,算法的大致過程是想辦法從當前序列進入下一個剛好比其大或者剛好比其小的序列...很自然我們想到要把序列后面大的字符交和前面小的字符交換就會使序列變大,為了使其剛好變大,可以把交換后的字符從交換位置起至最后都排序一下,現在的問題是我們如何選取2個字符交換...正確的想法是,我們從最后面開始往前面看,尋找一個最長的遞增序列,找到之后,我們只需要選取遞增序列前面的那個字符chBefore和遞增序列里面的一個最小的比chBefore大的字符交換即可...交換之后,將新的遞增序列排序一下即可...
為什么這樣做了,因為從后往前看的遞增序列,是不能交換2個字符讓當前序列變大的,所以必須選取最長遞增序列前面的那個字符交換...
POJ百練 - 1833 的代碼如下:
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define MAX (1024 + 10)
using namespace std;
int nInput[MAX];
void GetNext(int* nInput, int nLen)
{
int i = nLen - 2;
while (i >= 0)
{
if (nInput[i] >= nInput[i + 1])
{
--i;
}
else
{
int k = i + 1;
for (int j = nLen - 1; j > i; --j)
{
if (nInput[j] > nInput[i] && nInput[j] < nInput[k])
{
k = j;
}
}
swap(nInput[i], nInput[k]);
sort(nInput + i + 1, nInput + nLen);
return;
}
}
sort(nInput, nInput + nLen);
}
int main()
{
int nCases;
scanf("%d", &nCases);
while (nCases--)
{
int nLen;
int nK;
scanf("%d%d", &nLen, &nK);
for (int i = 0; i < nLen; ++i)
{
scanf("%d", &nInput[i]);
}
for (int i = 0; i < nK; ++i)
{
GetNext(nInput, nLen);
}
for (int i = 0; i < nLen; ++i)
{
printf("%d%s", nInput[i], i == nLen - 1 ? "\n" : " ");
}
}
return 0;
}