這一節關注根據key定位到數據進行刪除的整個流程。
先來看這個過程的流程圖,其實很簡單,包括以下幾個按部就班的步驟:

a) 首先,根據key查找對應的記錄,這個在上一節已經完整的介紹過了,當時也提到,查找操作是后續進行刪除和插入新數據時的基礎。
如果沒有找到記錄,說明原來就沒有,那么就不必繼續下去了。
假設現在找到了所要刪除的數據,接著以下幾步:
b) 將該記錄的magic number置為0xb0,第一節講解hash數據庫概述的時候提到過,每條記錄的頭部信息中有兩種不同magic number,根據這個判斷一條記錄是否被刪除了,現在將這個magic number置為0xb0就是表示這條記錄已經被刪除了。
c) 將這條被刪除的記錄插入到free pool數組中的合適位置,這是下一節的重點,這里先知道這個操作就好。
d) 上一節提到過,同一個bucket index是以二叉樹形式組織在一起的,雖然不是平衡的二叉樹,但是刪除了一個數據之后會破壞二叉樹的性質,所以需要在二叉樹中找到合適的記錄來替換刪除這條記錄之后剩下的位置。
熟悉數據結構與算法的都知道,一個排序二叉樹如果按照中序遍歷的話,那么是有序的。所以要在刪除一個記錄之后仍然保持排序二叉樹的有序性,是刪除操作的重點,下面就是TC中刪除一個記錄時的調整算法:
if rec.left is not null and rec.right is null
child = rec.left
else if rec.left is null and rec.right is not null
child = rec.right
else if rec.left is null and rec.right is null
child = null
else
child = rec.left
right = rec.right
rec.right = child
while (rec.right is not null)
rec = rec.right
rec.right = right
replace rec's original place with child
也可以從下圖中來理解當刪除一個記錄時,它的左右子節點都不為空時的處理:
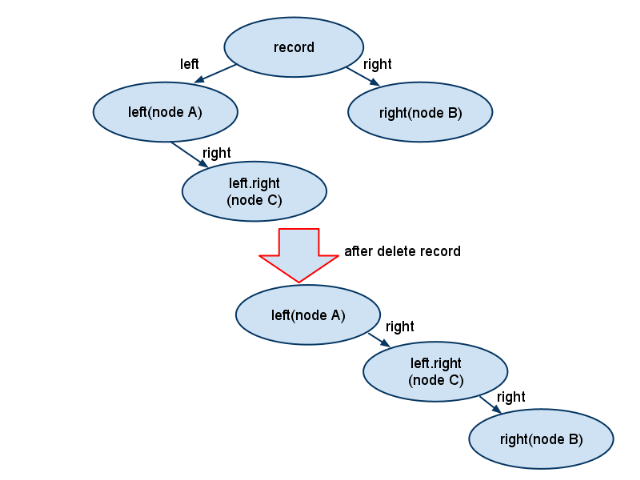
從圖中可以看出,當所要刪除的節點左右子節點都不為空時,會去尋找左子樹中的最右邊的子節點,然后將待刪除記錄的右子樹變成這個最右子節點的右子樹。
需要注意到的是,經典的數據結構算法中,當在排序二叉樹中刪除一個節點之后,所做的調整與上面的流程有所不同,雖然也是找到的原記錄的左子樹的最右節點,但是是將這個最右節點直接替換掉原來記錄的位置,也就是如下圖:
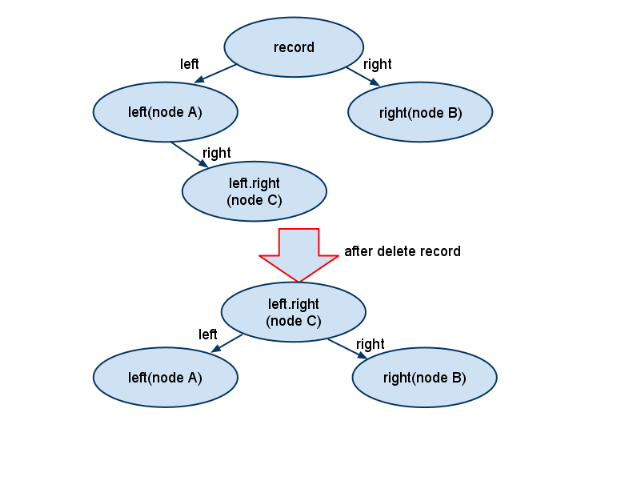
所以,這里出現了一個新的問題,TC中的調整算法是有可能導致刪除記錄之后二叉樹不平衡的,那么為什么不選用第二種方法呢?
我的理解是:
1) 如前一節所述,TC中的二叉樹本來就不是必然平衡的,所以TC中的這種調整算法有可能會有“負負得正”的結果。
2)第二種經典的做法中,需要的調整包括:a)將最右子節點從原來的父節點上刪除 b)最右子節點要替換原記錄的位置,那么要將原記錄的左右子樹分別賦值變為最右子節點的左右子樹。上面的這個調整,每次調整都是需要修改節點的,而每次修改都會有對磁盤的I/O操作。
而第一種做法呢,僅需要一次修改操作-----將原記錄的右子樹變成最右子節點的右子樹即可。
綜合這幾個因素,TC選擇了I/O較少的做法。
我不清楚我的理解是否合理,歡迎補充。
e)刪除了記錄,也跳整了樹的結構之后,最后的工作就是更新數據庫文件header的信息---因為當前記錄少了一條。
最后分析一下整個刪除操作的最壞復雜度,還是以1G的bucket對16G的數據庫文件記錄為例:
1)首先查找元素,前面一節說了,需要O(4)次磁盤I/O+O(1)讀取內存
2)接著置所刪除記錄的magic number,一次磁盤I/O
3)將刪除插入到合適的free pool位置,這個下一節會提到,是在內存中進行的。
4)調整樹結構,在所刪除記錄左右子樹都存在的情況下,首先要找到最右子節點,這又是一個O(4)的磁盤I/O操作,最后將原記錄的右子樹賦值給最右子節點,又是一次磁盤I/O。不過,上面這個推斷與前面是有矛盾的,假如在第一步查找中已經需要O(4)的代價才能定位到所刪除元素了,那么最后的這個調整根本沒有必要了。