   /**//* /**//*
 題意:給出上面n個數,下面n個數,求完美匹配的最大邊最小。邊權定義為兩個數相乘。可以負數 題意:給出上面n個數,下面n個數,求完美匹配的最大邊最小。邊權定義為兩個數相乘。可以負數
 應該有點YY的 應該有點YY的
 先分一下情況 先分一下情況
 同號:大*小 才能使最大那個最小 同號:大*小 才能使最大那個最小
 異號:小*小 才能使最大那個最小 異號:小*小 才能使最大那個最小
 一點貪心的思想 一點貪心的思想
 上面的那些正數跟下面的負數匹配 上面的那些正數跟下面的負數匹配
 上面的那些負數跟下面的正數匹配 上面的那些負數跟下面的正數匹配
 這樣剩下來的(當然可以沒有剩下),肯定是同號的,而且這些數更接近于0 這樣剩下來的(當然可以沒有剩下),肯定是同號的,而且這些數更接近于0

 現在再來看那些 正數*負數 的情況 現在再來看那些 正數*負數 的情況
 剛才提到“小*小 才能使最大那個最小”,而且越小的話越好 剛才提到“小*小 才能使最大那個最小”,而且越小的話越好
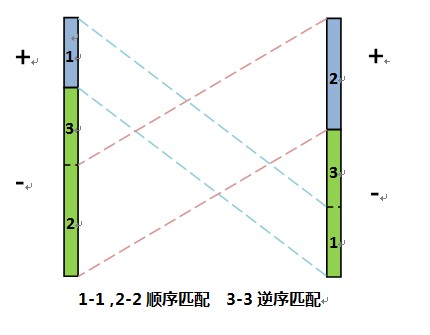
 所以上面那些最大的正數跟下面那些最小的負數匹配(順序匹配,大-大,小-小) 所以上面那些最大的正數跟下面那些最小的負數匹配(順序匹配,大-大,小-小)
 同理,上面的那些最小的負數跟下面那些最大的正數匹配 同理,上面的那些最小的負數跟下面那些最大的正數匹配

 就這樣先排序,然后找出各自的0的位置 就這樣先排序,然后找出各自的0的位置
 再分類一下即可 再分類一下即可
 */ */
 #include<cstdio> #include<cstdio>
 #include<cstring> #include<cstring>
 #include<algorithm> #include<algorithm>
 using namespace std; using namespace std;

 const int MAXN = 100010; const int MAXN = 100010;
 const long long INF = 1LL<<62; const long long INF = 1LL<<62;

 int A[MAXN],B[MAXN]; int A[MAXN],B[MAXN];

 int main() int main()
   { {
 int n; int n;
 while(~scanf("%d",&n)) while(~scanf("%d",&n))
   { {
 for(int i=0;i<n;i++) for(int i=0;i<n;i++)
 scanf("%d",&A[i]); scanf("%d",&A[i]);
 for(int i=0;i<n;i++) for(int i=0;i<n;i++)
 scanf("%d",&B[i]); scanf("%d",&B[i]);
 sort(A,A+n); sort(A,A+n);
 sort(B,B+n); sort(B,B+n);
 long long ans=-INF; long long ans=-INF;
 int ka=lower_bound(A,A+n,0)-A; int ka=lower_bound(A,A+n,0)-A;
 int kb=lower_bound(B,B+n,0)-B; int kb=lower_bound(B,B+n,0)-B;
 int d1=min(n-ka,kb); int d1=min(n-ka,kb);

 int a1=n-1,b1=d1-1; int a1=n-1,b1=d1-1;
 for(int cnt=0;cnt<d1;cnt++) for(int cnt=0;cnt<d1;cnt++)
   { {
 ans=max(ans,(long long)A[a1--]*B[b1--]); ans=max(ans,(long long)A[a1--]*B[b1--]);
 } }
 int d2=min(ka,n-kb); int d2=min(ka,n-kb);
 int a2=d2-1,b2=n-1; int a2=d2-1,b2=n-1;
 for(int cnt=0;cnt<d2;cnt++) for(int cnt=0;cnt<d2;cnt++)
   { {
 ans=max(ans,(long long)A[a2--]*B[b2--]); ans=max(ans,(long long)A[a2--]*B[b2--]);
 } }
 a1=n-1-d1,b1=d1; a1=n-1-d1,b1=d1;
 for(int cnt=0;cnt<n-d1-d2;cnt++) for(int cnt=0;cnt<n-d1-d2;cnt++)
   { {
 ans=max(ans,(long long)A[a1--]*B[b1++]); ans=max(ans,(long long)A[a1--]*B[b1++]);
 } }
 printf("%I64d\n",ans); printf("%I64d\n",ans);
 } }
 return 0; return 0;
 } }

|
|
常用鏈接
隨筆分類
Links
搜索
最新評論

|
|