Bernoulli EquationThe Bernoulli Equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids. The qualitative behavior that is usually labeled with the term "Bernoulli effect" is the lowering of fluid pressure in regions where the flow velocity is increased. This lowering of pressure in a constriction of a flow path may seem counterintuitive, but seems less so when you consider pressure to be energy density. In the high velocity flow through the constriction, kinetic energy must increase at the expense of pressure energy. 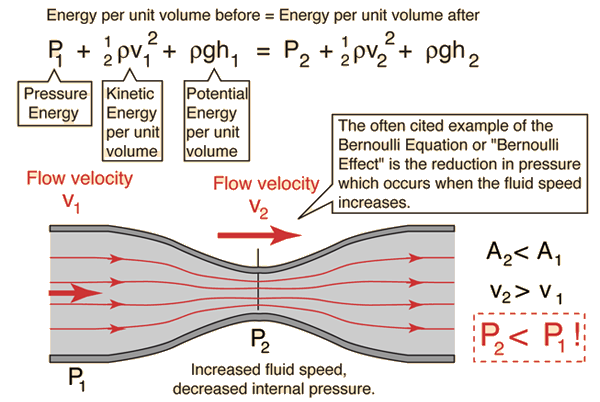 Steady-state flow caveat: While the Bernoulli equation is stated in terms of universally valid ideas like conservation of energy and the ideas of pressure, kinetic energy and potential energy, its application in the above form is limited to cases of steady flow. For flow through a tube, such flow can be visualized as laminar flow, which is still an idealization, but if the flow is to a good approximation laminar, then the kinetic energy of flow at any point of the fluid can be modeled and calculated. The kinetic energy per unit volume term in the equation is the one which requires strict constraints for the Bernoulli equation to apply - it basically is the assumption that all the kinetic energy of the fluid is contributing directly to the forward flow process of the fluid. That should make it evident that the existence of turbulence or any chaotic fluid motion would involve some kinetic energy which is not contributing to the advancement of the fluid through the tube. It should also be said that while conservation of energy always applies, this form of parsing out that energy certainly does not describe how that energy is distributed under transient conditions. A good visualization of the Bernoulli effect is the flow through a constriction, but that neat picture does not describe the fluid when you first turn on the flow. Another approximation involved in the statement of the Bernoulli equation above is the neglect of losses from fluid friction. Idealized laminar flow through a pipe can be modeled by , which does include viscous losses resulting in a lowering of the pressure as you progress along the pipe. The statement of the Bernoulli equation above would lead to the expectation that the pressure would return to the value P1 past the constriction since the radius returns to its original value. This is not the case because of the loss of some energy from the active flow process by friction into disordered molecular motion (thermal energy). More accurate modeling can be done by combining the Bernoulli equation with Poiseuille's law. A real example which might help visualize the process is the pressure monitoring of the flow through a constricted tube. |