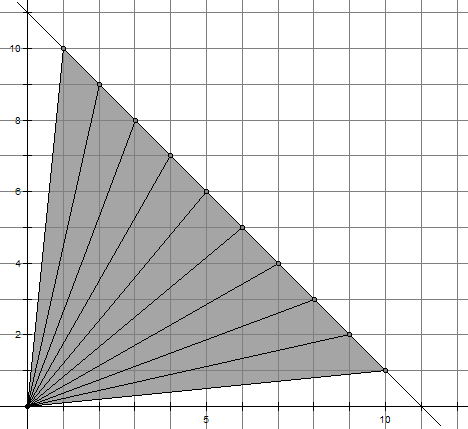
考慮直線x+y=n,其中n是一個素數。這條直線將恰好通過第一象限里的n-1個格點(如上圖,圖中所示的是n=11的情況)。將這n-1個點分別和原點相連,于是得到了n-2個灰色的三角形。仔細數數每個三角形內部的格點數,你會發現一個驚人的事實:每個三角形內部所含的格點數都是一樣多。這是為什么呢?
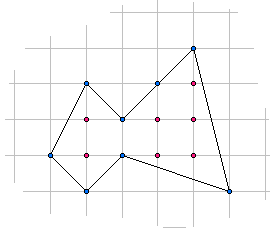
Pick定理是說,在一個平面直角坐標系內,如果一個多邊形的頂點全都在格點上,那么這個圖形的面積恰好就等于邊界上經過的格點數的一半加上內部所含格點數再減一。例如,上圖多邊形的邊界上有8個格點,內部含有7個格點,那么其面積就等于8/2+7-1=10。我們曾經在這里看到過一個非常神奇非常詭異的證明。這個定理有一些非常巧妙的應用。在上面的問題里,所有三角形都是等底等高的,因此它們的面積都相等。另外,注意到x與y的和是一個素數,這表明x和y是互素的(否則x+y可以提出一個公因數d,與和為素數矛盾),也就是說(x,y)和原點的連線不會經過其它格點。既然所有三角形的面積都相等,邊界上的格點數也相等,由Pick定理,我們就能直接得出每個三角形內部的格點數也相等了。
另一個有趣的問題則是,一個n*n的正方形最多可以覆蓋多少個格點?把這個正方形中規中矩地放在直角坐標系上,顯然能夠覆蓋(n+1)^2個格點。貌似這已經是最多的了,不過如何證明呢?利用Pick定理,我們能夠很快說明它的最優性。注意到由于任兩個格點間最近也有一個單位的間距,再考慮到正方形的周長為4n,因此該正方形的邊界上最多有4n個格點。把正方形邊界上的格點數記作B,內部所含格點數記為I,于是它所能覆蓋的總格點數等于I+B,由于I+B = I+B/2-1 + B/2+1 ≤ n^2 + 4n/2 + 1 = (n+1)^2,結論立即得證。
一個東西最出神入化的運用還是見于那些與它八桿子打不著的地方。Farey序列是指把在0到1之間的所有分母不超過n的分數從小到大排列起來所形成的數列,我們把它記作F_n。例如,F_5就是
0/1, 1/5, 1/4, 1/3, 2/5, 1/2, 3/5, 2/3, 3/4, 4/5, 1/1
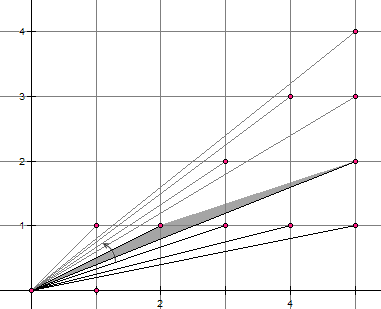
Farey序列有一個神奇的性質:前一項的分母乘以后一項的分子,一定比前一項的分子與后一項分母之積大1。用Pick定理來證明這個結論異常簡單。把分母不超過n的每一個0和1之間的分數都標在平面直角坐標系上,例如0/1就對應點(1,0),1/5就對應點(5,1)。考慮一根從原點出發的射線由x軸正方向逆時針慢慢轉動到y軸正方向,這根射線依次掃過的標記點恰好就是一個Farey序列(因為Farey序列相當于是給每個標記點的斜率排序)。考慮這根射線掃過的兩個相鄰的標記點,它們與原點所組成的三角形面積一定為1/2——由于分數都是最簡分數,因此它們與原點的連線上沒有格點;又因為這是射線掃過的兩個相鄰的標記點,因此三角形內部沒有任何格點。另外注意到,由于三角形面積等于叉積的一半,因此兩個點(m,n)和(p,q)與原點組成的三角形面積應該為(mq-np)/2。于是,對于Farey序列的兩個相鄰分數n/m和q/p,我們有(mq-np)/2 = 1/2,即mq-np=1。