題意:
有一些圓形的鏡子,一束光線射進來,試模擬光線的反射過程
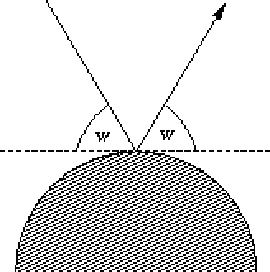
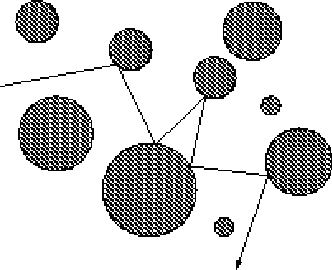
測試數據:
/Files/yzhw/reflect.rar解法:
這個問題首先從整體上看應該用迭代法,每次確定v向量和初始位置,然后循環10次即可
下面解決2個問題:
1、求與某個圓的的第一個交點
2、求新的速度矢量
對以第一個問題,我們設參數k,然后列方程:
設x',y'為圓心坐標,r為半徑。x0,y0為初始點,(dx,dy)為速度矢量
那么有
(x0+kdx-x')
2+(y0+kdy-y')
2=r
2
如果delta<0,那么說明直線與圓沒有交點
否則取k=(-b-sqrt(delta))/2a
如果k<=0,則說明交點在射線的反方向或者交點就在原來的位置,不滿足題意
第一個問題算比較好的解決了。
第二個問題我覺得比較簡單的方法是利用向量的旋轉矩陣
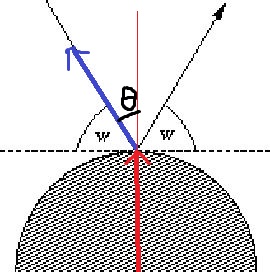
藍色的向量和紅色的向量在知道交點后是很容易算出的。cosθ利用向量夾角公式也不是問題,由于θ肯定是銳角,sinθ也不是問題了。
然后就可以利用旋轉矩陣將紅色的向量右旋得到目標速度向量(不一定是右旋,如果光線從紅色向量右側射入,那么就要左旋了。判斷左右可以用叉積或者干脆直接將兩個向量都求出,選擇與原來那個不同的向量即可)。
旋轉矩陣(左旋):
[cosθ -sinθ]
[sinθ cosθ]
有一點要注意:精度卡到1e-8就夠了,求sin的時候sqrt(1-cos*cos+
eps),不然可能會出現-0.000000001這種情況。。。
代碼:
1 # include <cstdio>
# include <cstdio>
2 # include <cmath>
# include <cmath>
3 # include <cstdlib>
# include <cstdlib>
4 using namespace std;
using namespace std;
5 # define eps 1e-8
# define eps 1e-8
6 struct circle
struct circle
7

 {
{
8 double x,y,r;
double x,y,r;
9 }cir[30];
}cir[30];
10 int n,id[30];
int n,id[30];
11 double tmp[30][4];
double tmp[30][4];
12 double dx,dy,x0,y00;
double dx,dy,x0,y00;
13 inline double dis(double x1,double y1,double x2,double y2)
inline double dis(double x1,double y1,double x2,double y2)
14

 {
{
15 return (((x1)-(x2))*((x1)-(x2))+((y1)-(y2))*((y1)-(y2)));
return (((x1)-(x2))*((x1)-(x2))+((y1)-(y2))*((y1)-(y2)));
16 }
}
17 inline bool less(double n1,double n2)
inline bool less(double n1,double n2)
18

 {
{
19 return (fabs((n1)-(n2))>eps&&(n1)<(n2));
return (fabs((n1)-(n2))>eps&&(n1)<(n2));
20 }
}
21 inline bool gt(double n1,double n2)
inline bool gt(double n1,double n2)
22

 {
{
23 return (fabs((n1)-(n2))>eps&&(n1)>(n2));
return (fabs((n1)-(n2))>eps&&(n1)>(n2));
24 }
}
25 void cal(circle &pos,int &count,int _id)
void cal(circle &pos,int &count,int _id)
26

 {
{
27 double b=2.0*((x0-pos.x)*dx+(y00-pos.y)*dy),a=dx*dx+dy*dy,c=(x0-pos.x)*(x0-pos.x)+(y00-pos.y)*(y00-pos.y)-pos.r*pos.r;
double b=2.0*((x0-pos.x)*dx+(y00-pos.y)*dy),a=dx*dx+dy*dy,c=(x0-pos.x)*(x0-pos.x)+(y00-pos.y)*(y00-pos.y)-pos.r*pos.r;
28 double delta=b*b-4.0*a*c;
double delta=b*b-4.0*a*c;
29 if(less(delta,0)) return;
if(less(delta,0)) return;
30 else
else
31

 {
{
32 double k=(-b-sqrt(delta))/2.0/a;
double k=(-b-sqrt(delta))/2.0/a;
33 if(!gt(k,0)) return;
if(!gt(k,0)) return;
34 id[count]=_id;
id[count]=_id;
35 tmp[count][0]=x0+dx*k;
tmp[count][0]=x0+dx*k;
36 tmp[count][1]=y00+dy*k;
tmp[count][1]=y00+dy*k;
37 double x2=tmp[count][0]-pos.x,y2=tmp[count][1]-pos.y;//連心線向量
double x2=tmp[count][0]-pos.x,y2=tmp[count][1]-pos.y;//連心線向量
38 double x1=x0-tmp[count][0],y1=y00-tmp[count][1];//原向量
double x1=x0-tmp[count][0],y1=y00-tmp[count][1];//原向量
39 double cs=(x1*x2+y2*y1)/sqrt(x1*x1+y1*y1)/sqrt(x2*x2+y2*y2);//計算cos
double cs=(x1*x2+y2*y1)/sqrt(x1*x1+y1*y1)/sqrt(x2*x2+y2*y2);//計算cos
40 double sn=sqrt(1-cs*cs);//計算sin
double sn=sqrt(1-cs*cs);//計算sin
41 if(less(x1*y2-x2*y1,0))//點積判斷左右情況
if(less(x1*y2-x2*y1,0))//點積判斷左右情況
42 x1=cs*x2+sn*y2,y1=-sn*x2+cs*y2;
x1=cs*x2+sn*y2,y1=-sn*x2+cs*y2;
43 else if(gt(x1*y2-x2*y1,0))
else if(gt(x1*y2-x2*y1,0))
44 x1=cs*x2-sn*y2,y1=sn*x2+cs*y2;
x1=cs*x2-sn*y2,y1=sn*x2+cs*y2;
45 else x1=x2,y1=y2;
else x1=x2,y1=y2;
46 k=sqrt(x1*x1+y1*y1);
k=sqrt(x1*x1+y1*y1);
47 x1/=k;
x1/=k;
48 y1/=k;
y1/=k;
49 tmp[count][2]=x1;
tmp[count][2]=x1;
50 tmp[count][3]=y1;
tmp[count][3]=y1;
51 count++;
count++;
52 }
}
53 }
}
54 int main()
int main()
55

 {
{
56 //freopen("reflect.in","r",stdin);
//freopen("reflect.in","r",stdin);
57 //freopen("ans.txt","w",stdout);
//freopen("ans.txt","w",stdout);
58 int count=1;
int count=1;
59 while(true)
while(true)
60

 {
{
61 scanf("%d",&n);
scanf("%d",&n);
62 if(!n) break;
if(!n) break;
63 for(int i=0;i<n;i++)
for(int i=0;i<n;i++)
64 scanf("%lf%lf%lf",&cir[i].x,&cir[i].y,&cir[i].r);
scanf("%lf%lf%lf",&cir[i].x,&cir[i].y,&cir[i].r);
65 scanf("%lf%lf%lf%lf",&x0,&y00,&dx,&dy);
scanf("%lf%lf%lf%lf",&x0,&y00,&dx,&dy);
66 printf("Scene %d\n",count++);
printf("Scene %d\n",count++);
67 for(int t=1;t<=11;t++)
for(int t=1;t<=11;t++)
68

 {
{
69 int c=0;
int c=0;
70 for(int i=0;i<n;i++)
for(int i=0;i<n;i++)
71 cal(cir[i],c,i);
cal(cir[i],c,i);
72 if(c==0)
if(c==0)
73

 {
{
74 printf("inf\n\n");
printf("inf\n\n");
75 break;
break;
76 }
}
77 else if(t!=11)
else if(t!=11)
78

 {
{
79 double len=1e16;
double len=1e16;
80 int target;
int target;
81 for(int i=0;i<c;i++)
for(int i=0;i<c;i++)
82

 {
{
83 if(less(dis(x0,y00,tmp[i][0],tmp[i][1]),len))
if(less(dis(x0,y00,tmp[i][0],tmp[i][1]),len))
84 len=dis(x0,y00,tmp[i][0],tmp[i][1]),target=i;
len=dis(x0,y00,tmp[i][0],tmp[i][1]),target=i;
85 }
}
86 printf("%d ",id[target]+1);
printf("%d ",id[target]+1);
87 x0=tmp[target][0];
x0=tmp[target][0];
88 y00=tmp[target][1];
y00=tmp[target][1];
89 dx=tmp[target][2];
dx=tmp[target][2];
90 dy=tmp[target][3];
dy=tmp[target][3];
91 // printf("%.4f %.4f %.4f %.4f\n",x0,y00,dx,dy);
// printf("%.4f %.4f %.4f %.4f\n",x0,y00,dx,dy);
92 }
}
93 else printf("
else printf(" \n\n");
\n\n");
94 }
}
95 }
}
96 return 0;
return 0;
97 }
}
98
99
100