1.技能快捷键
2.判断技能CD�Q�范��_���Ҏ��技能类型设�|�技能目标,eg.以自�w��ؓ中心的AOE技能,目标是自�w?br />3.向Server发送TryUseSkill消息
Server
1.收到Client消息,使用的技能压入到‘技能处理列�?#8216;�?br /> m_skillTaskMgr.Push( TaskType_Skill, target, position, skillID, skillLvl )
2.在玩家每一帧中调用 m_skillTaskMgr.GetTask() 处理所有类型的��d���Q�包括技�?/p>
3.判断使用技能的一些条�Ӟ��eg.技能目标,技能范�?..
都满���_��Client发送MsgIntonateStart开始吟唱消�?br />
Server:
1.目标�q�入视野�Q�如果目标正在吟唱或�l�持��法�Q�将此状态消息MsgSkillStatus发给自己
EnterMySight(pTarget)
if ( pTarget->IsIntonate() || pTarget->IsHoldSkill() )
pTarget->SendSkillStatusTo( pMe )
Client
1.接受到Server技能吟唱消�?MsgIntonateStart MsgSkillStatus
参数:iSkillID, iSkillLvl, srcPlayerID, tagPlayerID, iPercent
1). 若是自己吟唱�Q�显�C�吟��p��度条 UIProgressBar::Show(...)
2). 加入到动作队列中�{�待处理 GetActionQueue()->Push_Intonate(...)
2. 每�� HandleActionQueue 中处�?‘技能吟�?#8217;Intonate
1�Q�保存吟��q��技�?skillID, skillLvl
2�Q�播攑�ƈ记录吟唱的特�?iSkillEffectID = PlayEffect(...)
3�Q�切换到吟唱动作 SwitchActionStatus( Intonate, ...)
3. 吟唱�l�束 条�g诸如�Q�EndIntonate IntonateInterrupt HoldSkillEnd HoldSkillCancel Dead
1).切换动作到idle状�?br /> 2).清除播放中的吟唱�Ҏ�� GetEffectMgr()->ReleaseEffect( iSkillEffectID )
本�h��x��动实��C��世界坐标�p�M��的一点到屏幕坐标�pȝ��转换 , �|�上的资料都是在讲解固定���线的渲染过�E?span style="line-height: normal"> , 本�h的需求�ƈ不需要做 背面拣选裁剪等操作 , 所以自己来写一�?span style="line-height: normal"> ,
��M�����程�?span style="line-height: normal">
世界坐标�p?span style="line-height: normal">->视图坐标�p?span style="line-height: normal">->投媄�q�面坐标�p?span style="line-height: normal">->屏幕坐标�p?span style="line-height: normal">
世界坐标�p?/span>->视图坐标�p?/span>
见本人的另外一��?br style="line-height: normal" />
详述世界坐标�p�d��视图坐标�p?摄像机坐标系)的矩阵变�?/a>
视图坐标�p?/span>->投媄�q�面坐标�p?/span>(透视投媄)
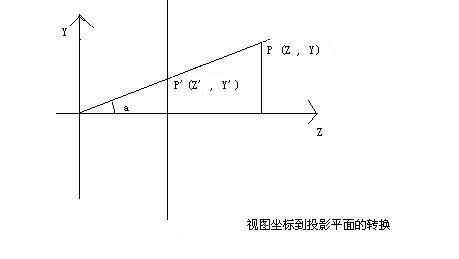
投媄�q�面, �?span style="line-height: normal">D3D�?span style="line-height: normal">Z = 1 且与X, Y轴��^行的�q�面 , �׃��透视投媄, 灭点在视囑֝�标系的原�?span style="line-height: normal">, ��L��一点在该��^面的投媄�?span style="line-height: normal"> .
已知视图坐标�pȝ��一�?span style="line-height: normal">P(Y , Z) , �?在投影��^面的�?span style="line-height: normal">P(Y’ , Z’) , �?span style="line-height: normal">a未知 ,�?span style="line-height: normal">
�׃��角�Ş�怼�可得 , (X Z的坐标��u与上囄����?span style="line-height: normal"> , 只是�?span style="line-height: normal">Y换成X而已)
Y’= Y * Z’ / Z
X’= X * Z’ / Z
D3D中投影��^�?span style="line-height: normal">Z’ =1, 所�?span style="line-height: normal">
Y’= Y / Z
X’= X / Z
Z’= 1
�׃��可得变换矩阵�?span style="line-height: normal">
1 0 0 0
0 1 0 0
0 0 1 1
0 0 0 0
投媄�q�面坐标�p?/span>->屏幕坐标�p?/span>
设投投媄�q�面最大高宽�ؓPh ,Pw ,通过Y轴的最大可视角�?span style="line-height: normal">a , 视截体的最�q?span style="line-height: normal">Z�?span style="line-height: normal"> Zf 则可得出 , 投媄�q�面的最大高�?span style="line-height: normal">Ph(Y轴方�?span style="line-height: normal">)
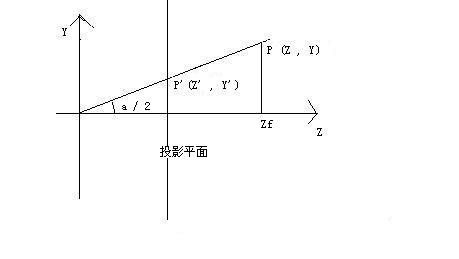
Ph= tan( a/2 ) * Zf
通过屏幕高宽�?span style="line-height: normal">Aspect, 求出最大宽�?span style="line-height: normal">Pw
Pw= Ph * Aspect
求得Ph , Pw , 我们可以得到投媄�q�面到屏�q���^面的转换比例(�׃��Ph , Pw仅是整个最大高宽的一�?span style="line-height: normal"> , 所以屏�q�最大高宽也除二)
Yscale= (Sh/2)/Ph
Xscale= (Sw/2)/Pw
则投影面上�Q意一�?span style="line-height: normal">P(X, Y) 到屏�q���^�?span style="line-height: normal">P’(X’ , Y’)的�{换�ؓ
X’= Sw/2 + X * Xscale
Y’= Sh/2 - Y * Yscale
PS.屏幕坐标原点在左上角
�׃��可得变换矩阵�?span style="line-height: normal">
Xscale 0 00
0 -Yscale 0 0
0 0 1 0
Sw/2 Sh/2 0 1
视口默认位置�?span style="line-height: normal">(0 , 0) , 不排除你会修�?span style="line-height: normal"> , 所以还要加上视口在windows�H�口的�v始位�|?span style="line-height: normal"> , 可以通过getviewport获得 所以矩阵应�?span style="line-height: normal">
Xscale 0 0 0
0 -Yscale 0 0
0 0 1 0
Port.x +Sw/2 Port.y +Sh/2 0 1
DirectX中投影变换D3DXMatrixPerspectiveFovLH�Q�)其实产生的变换矩阵不是将3D物体转换�?D�q�面画面的变换。实际上是把3D世界的物体变换到(1,1,0) (-1,1,0) (-1,-1,0) (1,-1,0) (1,1,1) (-1,1,1) (-1,-1,1) (1,-1,1)�q�个���盒子中。在Jim Adams 的著�?lt;Role playing games with DriectX 8.0>和Frank Luna 的著作中<Introduction to 3D Game Programming with DirectX9.0>都把�q�个变换矩阵讲成�?D�?D的变换。实际上在DirectX�?D�?D的变换是由SDK自己完成的。而我们要做的是把3D世界变换��C��面那个小盒子中�?/p>
�q�个变换矩阵是投影变换的预变换�?/span>
在DirectX中,把视口的高作�?D世界里面的长度:2.0f来��用的�Q�一个视点观察世界的视野范围在Y轴上无论什么情况下都是 -1.0f�?.0f�Q�这一点在后面来证明)。把视口的高作�ؓy��_����端坐标为(x�Q?�Q�,底端坐标为(x�Q?1�Q��?/span>
视口�Q�在�H�体中显�C?D的矩形范��_��可以通过D3DDevice的SetViewPort�Q�)来设�|�大���,默认的大����ؓ�H�体的大����?/span>
变换的过�E�就是把点的向量乘以变换矩阵�Q�可以得到这个点在新坐标�pȝ��对应向量�Q�在投媄变换矩阵中Z轴的��D���?~1之内�Q�也���是�?D世界里所有的炚w��会被投媄��C��上描�q�的���盒子中�?/span>
我们用函数D3DXMatrixPerspectiveFovLH来获得该“投媄变换”矩阵�?/span>
D3DXMATRIX * D3DXMatrixPerspectiveFovLH(
D3DXMATRIX *pOut,
FLOAT fovy,
FLOAT Aspect,
FLOAT zn,
FLOAT zf
);
其中参数fovy为y轴上的视角,Aspect为高宽比�Q�zn�����裁面�Q�zf�����裁面�?/span>
Y轴的视角�Q�在DirectX的帮助文档中描述fovy为filed of view in y direction�?/p>
高宽比:一般用于全屏显�C�,如果我们要让3D世界充满整个�H�口�Q�就必须让高宽比�{�于�H�口的高宽比�Q�例如让我们的窗口正常显�C?#8221;标准视野”[2X2 的一个面,��点坐标为(1�Q?�Q�,�Q?1�Q?�Q�,�Q?1�Q?1�Q�,�Q?�Q?1�Q�]�Q�我们必���L���H�口的高宽比讄����?�Q?�Q�这��P��标准视野���可以充满整个窗口,否则 会在左右留出�I�白�Q�这个空白是无法用VIEW�Q�WORLD变换所能填充的�Q�相当于word文档采用“文档”视图里面的两边的灰色区域�Q�是无法�~�辑的,在一般的3D�E�序里面是不允许出现�q�种情况的,但是我们的显�C�器的高宽比不是1�Q?�Q�而且大部分的用户也不习惯�?�Q?的窗口来使用�E�序�Q�我们需要调整这个标准视野,来适应我们的窗口大���,Aspect���是�q�个作用�Q�有一炚w��要说明的Aspect不等�?�Q�不代表标准视野��׃��是(1�Q?�Q�,�Q?1�Q?�Q�,�Q?1�Q?1�Q�,�Q?�Q?1�Q�,如果Aspect = 0.5 标准视野也还是(1�Q?�Q�,�Q?1�Q?�Q�,�Q?1�Q?1�Q�,�Q?�Q?1�Q�,只不�q�x轴上的单位长度的像素�?�?y轴上单位长度的像素值的2倍�?/p>
裁面的作�? 在Z轴方向上�Q�不昄���z坐标���于zn的或者大�?zf的点�?/span>
在上图中�Q����U�色的线为我们要昄���的面�Q�红色的弧就是上面函数fovy的夹角,当这个夹角�ؓ90°的时候,我们�H�口的视野�ؓ标准视野�Q�当夹角�~�小�Ӟ��可视范围���变���,如图�Q�从90°变�ؓ60°的时候,可视范围变小了,要显�C�的面,相对于可以范围变大了�Q�由于我们的�H�口是不变的�Q�也���是说实际显�C�的像素��g��变,要显�C�的面就相对于变大,fovy的值变���的�l�果���是把要昄���的面变大�?/span>
�?/span>fovy�?/span>0的时候呢�Q�视野就�?/span>0�Q�就是说什么都看不刎ͼ��H�口中显�C�的���是底色�?/span>
�?/span>fovy变大�?/span>180°的时候呢�Q?/span>视野的范围�ؓ视线夹角上的垂直�?/span>Z轴的且过点(0�Q?/span>0�Q?/span>1�Q�的�q�线。当视线夹角变大视野范围也变大,夹角���近�?/span>180°的时候视野范围趋�q�于无穷大,要显�C�的面相对于视野范围���是0�Q�也���是说羃���到最���就�?/span>0.所以我们在讑֮�fovy的��gؓ180°的时候也是什么都看不见,为底艌Ӏ?/span>
那大�?/span>180°的情况呢�Q�在我们的视野理��Z��是不存在�q�种情况的,当视角大�?/span>180°�Ӟ��视角�?/span>Z轴垂直的�q�线是不会过点(0�Q?/span>0�Q?/span>1�Q�的。但是函数放在我们面前,我们是可以输入大�?/span>180°的数��|���l�果会如何呢�Q?/span>
非常���奇的事情发生了�Q�我们的图以原点��Z��心旋转了180°�Q�这是无法用我们的视野理论来解释�?/span>,因�ؓ180°的视野范围就已经是个极限了,“���越极限”是只能在�q�告中出现的词汇�Q�如果能���越�Q�那��׃��叫极限了�Q?/span>P�Q��?/span>
�?/span>MSDN的文档中有这样一个数学公式:y-scale = cot�Q?/span>fovy/2�Q?/span>
�q�下���明白了�Q�当我们输入大于180°的时�?/span>cot的��gؓ负数。�?/span>x-scale = y-scale/ Aspect�?/span>.
也就是说�Q�一�?/span>3D世界的点�Q�在视野大于180°的作用下�Q�它的放�?/span>/�~�小倍数不变�Q�但是需要对X轴做一�ơ对�U�变换,�q�要�?/span>Y轴做一�ơ对�U�变换。相当于对原点做一�ơ对�U�变换�?/span>
拿到�q�个公式�Q�我们就可以对前面的标准做一个证明:
�?/span>fovy�?/span>90° Aspect = 1的时候,���是�?/span>y-scale = cot�Q?/span>45°�Q?/span> = 1
x-scale = 1�Q�这�?/span>y�?/span>x的羃放比都�ؓ1�Q�没有羃放。我们显�C����样一个面
{-1.0f, -1.0f, 0.0f},
{-1.0f, 1.0f, 0.0f},
{ 1.0f, 1.0f, 0.0f},
{-1.0f, -1.0f, 0.0f},
{ 1.0f, 1.0f, 0.0f},
{ 1.0f,-1.0f, 0.0f}
我们会发现无论怎么改变�H�口的高度,�q�个画面�?/span>Y轴方向上都会充满整个视口。(如果我们把视口的高度和宽度设�|�成一��L���Q�在X轴上也会充满整个视口�Q�所�?/span>DirectX会以视口的高度的二分之一作�ؓY轴的单位长度�?/span>
透过它的工作原理我们可以发现�Q�硬件��L���Ҏ��眼睛到目标的距离�Q�来玄奇最适合当前屏幕像素分��L率的囑ֱ�。假设一�?2768x32768的mipmap贴图�Q�当前屏�q�分辨率�?024*1024。眼睛距��ȝ��体比较近�Ӟ��mipmap最大也只可能从1024*1024的Mipmap囑ֱ�选取texel。再�ơ,当��用三�U�性过滤(trilinear�Q�时�Q�最大也只能讉K��2048*2048的图层选取texel�Q�来�?024*1024囑ֱ�中的像素�q�行�U�性插倹{�?img height="144" alt="" src="http://www.shnenglu.com/images/cppblog_com/wc250en007/D3D/MipMap1.jpg" width="514" border="0" />
��Z��加快渲染速度和减���图像锯齿,贴图被处理成�׃���p�d��被预先计���和优化�q�的囄����l�成的文�?�q�样的脓图被�U�Cؓ MIP map 或�?mipmap
多��渐进�U�理�׃���l�分辨率逐渐降低的纹理序列组成,每一�U�纹理宽度和高度都是上一�U�纹理宽度和高度的一半。宽和高不一定相�{�,也就是说�Q�这些纹理不一定都是正方�Ş�?/p>
Direct3D在纹理映���时�Q�自动选择一�q�与物体大小最接近的纹理进行渲染。当物体���L��影��^面较�q�时�Q�Direct3D会选择一张尺寸较���、分辨率较低的纹理进行渲染;当物体离投媄�q�面较近�Ӟ��Direct3D会选择一张尺寸较大、分辨率较高的纹理进行渲染。Direct3D���纹理序列看成一条多�U�渐�q�纹理链。链头处�U�理的分辨率最高,下一�U�往后依�ơ递减�Q�链���֤��U�理的分辨率最低�?/p>
Direct3D能估计出多��渐进�U�理链中哪幅�U�理的分辨率最接近惌���的输出结果,然后它将像素映射到纹理空间。当最�l�显�C�的囑�Ş大小介于��L��两��U�理囑�Ş之间�Ӟ��Direct3D���两�U�纹理的相应元素�q�行混合后显�C��?/span>
多��渐进�U�理�q���o能够有效�?span style="color: red">提高囑�Ş渲染速度
�Q?span style="color: red">当物体离投媄�q�面较远�Ӟ��Direct3D会选择一张尺寸较���的�U�理�q�行渲染�Q�而无需�l�过复杂的诸如各��异性纹理过�?/span>�Q��ƈ且由于这时纹理需要的昑֭�比不使用多��渐进�U�理时小�Q�因此能有效�?span style="color: red">减少�U�理载入昑֭�的时间�?/span>�~�点是对内存的要求比较高
讄���多��渐进�U�理�q���o方式
当最�l�显�C�的�U�理贴图大小介于��L��两��U�理之间�Ӟ��Direct3D能够取得两��U�理元素�q�行混合后显�C�,具体的�合方式由指定的多�U�渐�q�纹理过滤方式决定。可以调用函数IDirect3DDevice9::SetSamplerState()讄���多��渐进�U�理�q���o方式�Q�将�W�一个参数设为纹理层序号�Q�第二个参数设�ؓD3DSAMP_MIPFILTER表示多��渐进�U�理�q���o�Q�第三个参数设�ؓ在相�ȝ��理��之间的过滤方式,可取枚�D�c�d��D3DTEXTUREFILTERTYPE的�Q意倹{��下面的�C�Z��代码讄���盔R���U�理�U�之间的�q���o方式为线性过滤�?/p>
g_device->SetSamplerState(0, D3DSAMP_MIPFILTER, D3DTEXF_LINEAR);
如果���第三个参数设�ؓD3DTEXF_NONE�Q�那么就会一直��用最高一�U�的�U�理�Q�即���用多��渐进�U�理�q���o。如果将其设为D3DTEXF_POINT�Q�就会只使用与图元大���最匚w��的一�U�纹理。如果将其设为D3DTEXF_LINEAR�Q�Direct3D���将与图元大���最匚w��的两�U�纹理以�U�性方式�合�?/font>
需要注意的是,多��U�理�q���o是羃���和攑֤��q���o器的�l�合。例如,如果���羃���和�Ҏ���q���o器设为线性过滤,但是多��U�理�q���o方式设�ؓ最�q�点采样�Q�Direct3D��׃��选择与要昄���的纹理脓囑֤����最接近的纹理��别,在该�U�纹理上完成双线性纹理过滤,�q�将�l�果作�ؓ像素的倹{��如果将�~�小、放大过滤器和多�U�渐�q�纹理都讄���为线性过滤,则Direct3D��׃��在两个最接近的纹理��别上都进行双�U�性纹理过滤,然后再对盔R��两��U�理囑�Ş上对应的两个�U�理颜色�q�行加权�q�_���Q�最后的�l�果作�ؓ单个像素倹{��这�U��ؓ了图元中的一个像素,而结合了两幅�U�理�Q�共8个像素的技术,�U�Cؓ“三线性过�?#8221;�Q�因为它在纹理的三个方向----u�?v和纹理��别上都进行了�U�性过滤�?/font>
可以通过IDirect3DDevice9::SetSamplerState()函数讄���实际渲染时纹理过滤的最大��敎ͼ�其中需要将�W�二个参数设为D3DSAMP_MAXMIPLEVEL�Q�第三个参数设�ؓ实际渲染时纹理过滤的最大��数。下面的�C�Z��代码讄����U�理�?的最大多�U�纹理过滤����Cؓ16�?/p>
g_device->SetSamplerState(0, D3DSAMP_MAXMIPLEVEL, 16);
�q�可以通过���IDirect3DDevice9::SetSamplerState()的第二个参数设�ؓD3DSAMP_MIPMAPLODBIAS�Q�设�|�多�U�纹理映�����数偏�U�d��{��如果对某个�U�理映射讄���正偏�U�d��|��得到的图形结果就会比原来的更清晰�Q�但锯��更多�Q�反之设�����偏移��|��得到的图形结果就会更模糊�?/p>
代码�Q?a title="实例下蝲" href="/Files/wc250en007/D3D/TextQuad�U�理映射.rar">实例下蝲
-潘宏
-2009.12.31
-本�h水��^有限�Q�疏忽错误在所隑օ��Q�还请各位数学高手、编�E�高手不吝赐�?/span>
-email: popyy@netease.com
原文地址�Q?a >http://blog.csdn.net/popy007/article/details/5120158
一些网友写信给我希望能够了解固定流水线中世界空间到相机�I�间变换矩阵的具体推��D���E�。其实之前我在《向量几何在游戏�~�程中的使用6》中已经���单的把相机变换作��Z��个��用基理论的例子进行了说明�Q�但可能仍然不够具体。这���文章中�Q�我会尽力阐�q�相机变换的整个来龙去脉。希望能够对正在学习固定���水�U�的朋友们有所帮助。这里我们仍然会在推导相机变换之前介�l�几个理论知识,目的是�ؓ了更好的理解推导�q�程。我们马上开始!
什么是相机变换�Q?/span>
在流水线中,当物体从模型坐标通过世界矩阵变换��C��界空间之后,它将通过相机变换从世界空间变换到相机�I�间。下囄���固定���水�U�中�Q�蓝色框中的部分���是�q�个�q�程�?/span>

其实�Q�所谓的相机�I�间�Q�就是以相机作�ؓ坐标原点的一个参考系�Q�所以,从世界空间变换到相机�I�间�Q�就是把物体从世界坐标系�Q�变换到相机为原点的相机坐标�p�,如下图所�C��?/span>

左半部分是小人在世界�I�间中的位置�Q�右半部分是����h变换到相机空间后的位�|�。这��L��一个变换可以有很多�U�方式来实现�Q�欧拉相机系�l��?/span>UVN�pȝ���?/span>Two Points & A Twist�{�等。这里我们讨论最为广泛的UVN�pȝ��构徏相机矩阵�Q�如果读者对其他�Ҏ��感兴���,可以查找相关的资料。我们仍然讨�?/span>OpenGL的相机矩�늚�推导�Q�其�?/span>API可以�c�M��的推对{�?/span>
坐标转换公式
我们在《向量几何在游戏�~�程中的使用6》中提到了正交矩阵,�q�是在基理论基础上的一个概念(如果对基理论不是很熟悉,请参考《向量几何在游戏�~�程中的使用6》)。正交矩阉|��有列�Q�行�Q�向量构成了一�?strong>标准正交�?/strong>�Q�它的列向量都是互相正交�Q��ƈ且长度�ؓ1�Q�,因此�Q�可以把正交矩阵看成是对一个坐标系的描�q�。同�Ӟ��我们知道�Q?strong>同一个向量,在不同的��Z��面的坐标是不同的。因此,可以用正交矩阉|��代表坐标�p�(也可以看作基�Q�从而写出在�l�一的参考系�Q�全局坐标�p�)下同一个向量在不同��Z��的坐标�?/span>

上面的式子表�C�,参考系中向�?/span>v在基Q中的坐标�?/span>v’�Q�在�?/span>R中的坐标�?/span>v’’�Q�注意这里的环境下基矩阵是用列向量表�C�的�Q�这��L��乘之后的�l�果表示的是基向量的�U�性组合)。如下图�Q�黑色基表示的是参考系�Q�红色是�?/span>Q�Q�蓝色是�?/span>R�Q?/span>v是参考系中的一个向量�?/span>

��Z��让大家更清楚�Q�我举一个例子:

上式的意思是�Q�参考系中的向量v�Q�在�?/span>Q( 1 0 0 ), ( 0 1 0 ), ( 0 0 1)下的坐标�?/span>( 1 2 6 )�Q�在�?/span>R( 0 1 0 ), ( 0 0 1 ), ( 1 0 0 )下的坐标�?/span>( 2 6 1 )。注意,我们所讨论的所有基和向量的关系都只是线性表�C�的关系�Q�没有位�U�d���p�,因此我们�?/span>3D向量表示�Q�而不�?/span>4D的齐�ơ表�C�(如果寚w���ơ坐标不是很熟悉�Q�请参考《深入探索透视投媄变换》中的齐�ơ坐标部分)�?/span>
�q�样�Q�已知一个基Q和向�?/span>v在它之中的坐�?/span>v’�Q�以及另外一个基R�Q�我们可以通过v=Qv’=Rv’’公式来计��?/span>v’’�?/span>

上面���是�?/span>v’’的公式,注意到右辚w��要计���基R的逆矩�?/span>R^-1�Q�因为基R是正交矩阵,而正交矩�늚�一个重要性质���是逆等于�{�|�。因此,我们可以把它写成
![]()
�q�个公式���是坐标转换公式。特别地�Q�如�?/span>Q是和参考系相同的坐标系�Q?/span>3D�~�程中大多数情况下如此)�Q�比如世界坐标系�Q�则Q是一个单位矩�?/span>I�Q�则我们可以把它写成
![]()
�q�个坐标转换公式可以解释为:对于世界坐标�p�M��的向�?/span>v’�Q�它在坐标系R中的坐标�?/span>v’’。我们在后面会用到这个公式�?/span>
除了用正交矩阉|��阐述坐标转换�Q�我们还可以使用点积所代表�?strong>��q���E�度�Q?/span>colinear amount�Q�来描述坐标转换�Q?/span>AndréLaMothe的�?/span>Tricks Of The 3D Game Programming Gurus》)。这个理论基于点�U�的几何意义�Q�一个向量在另一个向量上的共�U�程度。比如两个向�?/span>v�?/span>s点积

几何意义���是v�?/span>s方向上的投媄长和s的长的乘�U�,或者是s�?/span>v方向上的投媄长和v的长的乘�U�(�U�的�W�号为:�?/span>v�?/span>s的角度小�?/span>90度,�U��ؓ正,如果是直角,�U��ؓ�Ӟ��否则������Q��?/span>

�q�一步地�Q�如�?/span>v是一个单位向量,则这个点�U�可以解释�ؓs�?/span>v方向上的投媄长;如果s是一个单位向量,则可以解释�ؓv�?/span>s方向上的投媄�ѝ��现在,我们把点�U�推�q�到基的层次上,把一个向�?/span>v’和一个基R的三个单位��u向量�q�行点积�Q�点�U�得到的三个值则表示�q�个向量在这个基下的坐标v’’

数学表达�?/span>

��h��意,��Z���?/span>v’能够和基的每一个��u向量�q�行点积�Q�我们必���L��基写成�{�|��Ş式,卌���向量乘法�Q�否则就变成了线性组合的形式。这个公式的意义���是世界�I�间中的向量v’和基R的��u向量�q�行点积从而得�?/span>v’�?/span>R下的��q���E�度——坐标v’’。这个公式和上面我们得到的坐标�{换公式一模一栗���实际上我们是从两个不同的方向解释同一个公式,希望你能够把两个方向都理解�?/span>
UVN�pȝ��
UVN�pȝ��本��n是一个基。如下图所�C�,三个基向�?/span>U�Q?/span>V�Q?/span>N分别指向相机的右斏V��上方和后方从而构成右手坐标系�Q�相机则处于坐标原点�?/span>

使用UVN�pȝ��可以非常方便的设�|�相机朝向。它的构������E�如下如所�C?/span>

在参考系下(�q�里是世界坐标系�Q�,我们�l�定相机的位�|?#8212;—eye�Q�被观察的小人的位置——lookat�Q�以及一个辅助向�?#8212;—参考系中表�C?#8220;上方”的向�?/span>up�Q�这个向量会影响U�?/span>V的生成,因�ؓ以后求出�?/span>V向量会在up�?/span>N向量所军_��的��^面上�Q�有兴趣可以自己证明一下)�Q�所以可以通过�q�个向量让相��Z�生不同的偏�{�?/span>

首先我们求出向量N
![]()
很简单,用目标位�|�减�ȝ��机的位置�Q�就是图中的步骤2。第3步,我们求出向量U。这一步需要��用辅助向�?/span>up�Q�如果不希望相机产生偏�{�Q�一般取(0, 1, 0)
![]()
U使用向量的叉乘实玎ͼ����是图中的步�?/span>3。最后,使用N�?/span>U计算出向�?/span>V
![]()
最后将计算出的U�Q?/span>V�?/span>N�q�行单位化,���得��C��相机�?/span>UVN�pȝ��。结合上面我们谈到的坐标转换理论�Q�我们可以把UVN�pȝ��看作是相机的基,从而可以方便的把一个向量在世界坐标和相机坐标进行�{换�?/span>
OpenGL�?/span>gluLookAt(eyex, eyey, eyez, lookatx, lookaty, lookatz, upx, upy, upz)�Ҏ�����是使用的上面的步骤�q�行相机矩阵的设�|�。它的前三个参数���是相机的位�|�向量,中间三个参数是所观察的目标位�|�向量,最后三个参数就是辅助向�?/span>up�?/span>
相机矩阵的推�?/span>
上面我们已经说明�?/span>UVN�pȝ���Q�标准流水线中就是��用了UVN�pȝ��来描�q�相机�?/span>U, V, N分别对应相机坐标�pȝ��三个基向量�?/span>
此外�Q�对于一个相机来��_��它在开始的时候和世界坐标�p�L��重合的,用户控制相机在世界空间中�U�d��之后�Q�相机的状态可以用两个属性来描述——朝向和位�|�。也���是��_��有了�q�两个属性,一个相机模型在世界中的状态就���定了。而这两个属性,我们用变换的理论来描�q�ͼ����是旋�{和��^�U�R��可以想象,对于世界中的��M��一个相机状态,我们都可以把它看成是�Q�相机先围绕自��n基原�Ҏ��转一定的角度�Q�然后��^�U�d��世界�I�间的某个地斏V��下囑ֱ��C�Z���q�个�q�程

图中�Q�红色是相机的基�Q�而黑色是世界的基�Q�也���是参考系。小人是世界中的一个物体。相机在�U�d��之前�Q�两个基是重合的。当相机在屏�q�中定位�Ӟ��它首先会�q�行朝向的确�?#8212;—旋�{�Q�然后进行位�|�的���定——�q�移。图中的Rotation�?/span>Translation两步���是相机定位时所发生的变换。可以看到相机相对于����h的运动。而当�q�行相机变换的时候,����h应该从世界基变换到相机的基里面。这��P��他应该进行一个相机定位的逆定位,先逆��^�U�d��人和相机�Q�然后再逆旋转小人和相机�Q�最后相机归位,����h随相机变��C��相机�I�间。这是由Inverse Translation�?/span>Inverse Rotation两个步骤完成的,�q�两个步骤就是相机变换。现在我们推��D��个变换。我们把关系写出来,相机本��n的变�?/span>C包括两个元素
![]()
其中T是��^�U�d��换,R是旋转变换。而相机变换是相机本��n变换的逆变�?/span>
![]()
�q�个C^-1���是我们要求出的相机变换。其�?/span>T^-1很容易求出,�?/span>

�?/span>R^-1���没有这么容易求出来了。所以,我们不求它,我们�?/span>UVN�pȝ��。什么意思?��L��上面的那张相机变换的图,当相机变换进行完Inverse Translation�q�一步之后,相机的原点和世界原点���重合了�Q�也���是处理完了关于�q�移的变换。接下来我们要做的是逆旋转,而其�?strong>逆旋转的目的�Q�就是要得到目前世界坐标中经�q�逆��^�U?/strong>的小人在相机坐标�p�M��的坐�?/strong>。是不是似曾相识�Q�我们的坐标变换理论���派上用��Z��。我们回忆上面坐标变换的公式
![]()
�q�个坐标转换公式可以解释为:对于世界坐标�p�M��的向�?/span>v’�Q�它在坐标系R中的坐标�?/span>v’’。那么,我们可以套用在这里:对于世界坐标中的已经�l�过逆��^�Uȝ��坐标v’�Q�它在相机坐标系R中的坐标�?/span>v’’。什么是相机坐标�p?/span>R�Q�就是我们的相机UVN�pȝ���Q�就�?/span>

则相机变换的完整公式���是
![]()
�q�里�Q?/span>v是小人在世界�I�间中的坐标�Q?/span>v’’是小人在相机�I�间中的坐标。则相机变换矩阵���是

��x���Q�我们就完成了相机矩�늚�推导。物体经�q�这个矩阵就从世界空间变换到了相机空��_���{�待���水�U�对它进行投影变换�?/span>OpenGL��׃��用了上面推导出的最后的那个矩阵。希望你能够理解�q�个推导�q�程�Q�如果你有什么问题或者不同的看法�Q�请一定给我发�?/span>J下次见!
 BOOL D3DXIntersectTri(
BOOL D3DXIntersectTri( CONST D3DXVECTOR3* p0, //��点1
CONST D3DXVECTOR3* p0, //��点1 CONST D3DXVECTOR3* p1,
CONST D3DXVECTOR3* p1, CONST D3DXVECTOR3* p2,
CONST D3DXVECTOR3* p2, CONST D3DXVECTOR3* pRayPos, //���线起始位置
CONST D3DXVECTOR3* pRayPos, //���线起始位置 CONST D3DXVECTOR3* pRayDir, //���线方向
CONST D3DXVECTOR3* pRayDir, //���线方向 FLOAT* pU, //三个�Ҏ���?br>
FLOAT* pU, //三个�Ҏ���?br> FLOAT* pV,
FLOAT* pV, FLOAT* pDist //���线��L����C��点位�|?br>
FLOAT* pDist //���线��L����C��点位�|?br> );
);
para �Q?/font>其中p0, p1, p2分别指向三角形的三个��点�Q�position为射�U��v点,direction为射�U�方向向量,u,v,��Z��炚w��心坐标,因�ؓ不可能只点到��点上,可能点在三角形范围内�Q�distance����v点到交点距离�Q�成功返回TRUE�Q�失败返回FALSE�?br>
vPickPos = v0 * ( 1-u-v) + v1*u + v2*v = v0 + u * (v1 - v0) + v * (v3 - v0);
特别注意�Q�方向向量必���Mؓ单位向量�Q�即pRayDir - pRayPos 为单位向量否则,pDist的值和向量长度成正比关�p?/span>
eg:
 D3DXVECTOR3 rayDir;
D3DXVECTOR3 rayDir; D3DXVECTOR3 vDest( 10,200,0.f);
D3DXVECTOR3 vDest( 10,200,0.f); D3DXVECTOR3 vSour( 10,200,-10.f );
D3DXVECTOR3 vSour( 10,200,-10.f ); rayDir = vDest - vSour;
rayDir = vDest - vSour; D3DXVec3Normalize( &rayDir, &rayDir ); //���方向向量化
D3DXVec3Normalize( &rayDir, &rayDir ); //���方向向量化 BOOL bHit = D3DXIntersectTri( &D3DXVECTOR3(0.0f, 0.0f, 0.5f),
BOOL bHit = D3DXIntersectTri( &D3DXVECTOR3(0.0f, 0.0f, 0.5f), &D3DXVECTOR3(250.0f, 250.0f, 0.5f),
&D3DXVECTOR3(250.0f, 250.0f, 0.5f), &D3DXVECTOR3(0.0f, 250.0f, 0.5f), //pos
&D3DXVECTOR3(0.0f, 250.0f, 0.5f), //pos &D3DXVECTOR3(10,200,-10.f ), //dir
&D3DXVECTOR3(10,200,-10.f ), //dir &rayDir,
&rayDir,  &fu,
&fu,  &fv,
&fv,  &t );
&t );游戏中应�?br>
 float CTerrain::GetZByXY( float fx,float fy )
float CTerrain::GetZByXY( float fx,float fy )

 {
{ //求出�W�几个方�?/span>
//求出�W�几个方�?/span> int x,y;
int x,y; x = fx / MAPTILESIZE;
x = fx / MAPTILESIZE; y = fy / MAPTILESIZE;
y = fy / MAPTILESIZE; if( x < 0 || x >= m_iMapWidth-1 )
if( x < 0 || x >= m_iMapWidth-1 ) return 0;
return 0; if( y < 0 || y >= m_iMapHeight-1 )
if( y < 0 || y >= m_iMapHeight-1 ) return 0;
return 0; 
 //�Ҏ��四顶�?/span>
//�Ҏ��四顶�?/span> D3DXVECTOR3 *pos[4];
D3DXVECTOR3 *pos[4]; pos[0] = &m_ppPointPos[ y ][ x ];
pos[0] = &m_ppPointPos[ y ][ x ]; pos[1] = &m_ppPointPos[ y ][ x + 1];
pos[1] = &m_ppPointPos[ y ][ x + 1]; pos[2] = &m_ppPointPos[ y + 1][ x + 1];
pos[2] = &m_ppPointPos[ y + 1][ x + 1]; pos[3] = &m_ppPointPos[ y + 1][ x ];
pos[3] = &m_ppPointPos[ y + 1][ x ];
 float fMaxZ;
float fMaxZ; fMaxZ = pos[ 0 ]->z ;
fMaxZ = pos[ 0 ]->z ; int iLoop;
int iLoop; for( iLoop = 1 ; iLoop < 4 ; iLoop ++ )
for( iLoop = 1 ; iLoop < 4 ; iLoop ++ )

 {
{ if( fMaxZ < pos[ iLoop ]->z )
if( fMaxZ < pos[ iLoop ]->z ) fMaxZ = pos[ iLoop ]->z;
fMaxZ = pos[ iLoop ]->z; }
}
 // 求眼睛和地�Ş�怺�位置�Q�注意单位化方向向量
// 求眼睛和地�Ş�怺�位置�Q�注意单位化方向向量 D3DXVECTOR3 vEye,vDir(0,0,-1);
D3DXVECTOR3 vEye,vDir(0,0,-1);
 vEye.x = fx;
vEye.x = fx; vEye.y = fy;
vEye.y = fy; vEye.z = fMaxZ + 10;
vEye.z = fMaxZ + 10;
 float fU,fV,fDis;
float fU,fV,fDis;
 if( !D3DXIntersectTri( pos[0],pos[1] ,pos[2],&vEye,&vDir, //三角�?
if( !D3DXIntersectTri( pos[0],pos[1] ,pos[2],&vEye,&vDir, //三角�? &fU,&fV,&fDis ) )
&fU,&fV,&fDis ) )

 {
{  if( !D3DXIntersectTri( pos[2],pos[3],pos[0],&vEye,&vDir, //三角�?
if( !D3DXIntersectTri( pos[2],pos[3],pos[0],&vEye,&vDir, //三角�? &fU,&fV,&fDis ) )
&fU,&fV,&fDis ) )

 {
{ return 0.0f;
return 0.0f; }
} else
else

 {
{ return vEye.z - fDis;
return vEye.z - fDis; }
} }
} else
else

 {
{ return vEye.z - fDis;
return vEye.z - fDis; }
} }
}参�?
地�Ş���撞计算:
一.如果是鼠标点��d���?
可将���线固定长度�q�分�D?然后用射�U�与每一个分�D�上的点所落在的地面tile(两个三角�?�q�行求交,
�怺�则返回对应位�|?否则�l�箋与下一个段上的�Ҏ��落在的地面tile求交
/*
0 1
---->
| \ |
| \ |
2 V --- 3
*/
�q�里不讨论点��d���q�求���线�Ҏ��与射�U�分�D�处�?只算求交
如下d3d求交得出uv,再求位置:
VECTOR3 vPickPos;
// 双���:
if( D3DXIntersectTri(&v0, &v1, &v3, &vOrig, &vDir, &u, &v, NULL) == TRUE)
{
vPickPos = v0 + u * (v1 - v0) + v * (v3 - v0);
return vPickPos.z;
}
// 左边:
if( D3DXIntersectTri(&v0, &v3, &v2, &vOrig, &vDir, &u, &v, NULL) == TRUE)
{
vPickPos = v0 + u * (v3 - v0) + v * (v2 - v0);
return vPickPos.z;
}
�?如果是仅是求地表某点高度
则可用uv重心求法(注意上述�W�一点的d3d的那个uv重心求法不太一�?他的uv跟他的向量走?)
float u = (fX-(int)fX);
float v = (fY-(int)fY);
float p0 = fHeight[0];
float p1 = fHeight[1];
float p2 = fHeight[2];
float p3 = fHeight[3];
if(u>v){ // 双���
return p0 + u * (p1 - p0) + v * (p3 - p1);;
}
else{ // 左边
return p0 + u * (p3 - p2) + v * (p2 - p0);
}
http://flipcode.spaces.live.com/blog/cns!8E578E7901A88369!1052.entry
