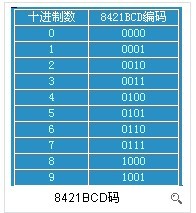
一、8421BCD碼 二進制編碼的十進制數(shù),簡稱BCD碼(Binarycoded Decimal). 這種方法是用4位二進制碼的組合代表十進制數(shù)的0,1,2,3,4,5,6 ,7,8,9 十個數(shù)符。4位二進制數(shù)碼有16種組合,原則上可任選其中的10種作為代碼,分別代表十進制中的0,1,2,3,4,5,6,7,8,9 這十個數(shù)符。最常用的BCD碼稱為8421BCD碼,8.4.2.1 分別是4位二進數(shù)的位取值。 右圖為十進制數(shù)和8421BCD編碼的對應關(guān)系表:
2、BCD碼的格式
計算機中的BCD碼,經(jīng)常使用的有兩種格式,即分離BCD碼,組合BCD碼。
所謂分離BCD碼,即用一個字節(jié)的低四位編碼表示十進制數(shù)的一位,例如數(shù)82的存放格式為:
_ _ _1 0 0 0 _ _ _ _0 0 1 0 其中_表示無關(guān)值。
組合BCD碼,是將兩位十進制數(shù),存放在一個字節(jié)中,例82的存放格式是1000 0010
3、BCD碼的加減運算
由于編碼是將每個十進制數(shù)用一組4位二進制數(shù)來表示,因此,若將這種BCD碼直接交計算機去運算,由于
計算機總是把數(shù)當作二進制數(shù)來運算,所以結(jié)果可能會出錯。例:用BCD碼求38+49。
解決的辦法是對二進制加法運算的結(jié)果采用"加6修正,這種修正稱為BCD調(diào)整。即將二進制加法運算的結(jié)果修正為BCD碼加法運算的結(jié)果,兩個兩位BCD數(shù)相加時,對二進制加法運算結(jié)果采用修正規(guī)則進行修正。修正規(guī)則:
(1)如果任何兩個對應位BCD數(shù)相加的結(jié)果向高一位無進位,若得到的結(jié)果小于或等于9,則該不需修正;若得到的結(jié)果大于9且小于16時,該位進行加6修正。
(2)如果任何兩個對應位BCD數(shù)相加的結(jié)果向高一位有進位時(即結(jié)果大于或等于16),該位進行加6修正.
(3)低位修正結(jié)果使高位大于9時,高位進行加6修正。
下面通過例題驗證上述規(guī)則的正確性。
用BCD碼求35+21 BCD碼求25+37 用BCD碼求38+49 用BCD碼求42+95
用BCD碼求91+83 用BCD碼求94+7 用BCD碼求76+45
兩個組合BCD碼進行減法運算時,當?shù)臀幌蚋呶挥薪栉粫r,由于"借一作十六"與"借一作十"的差別,將比正確的結(jié)果多6,所以有借位時,可采用"減6修正法"來修正.兩個BCD碼進行加減時,先按二進制加減指令進行運算,再對結(jié)果用BCD調(diào)整指令進行調(diào)整,就可得到正確的十進制運算結(jié)果。 實際上,計算機中既有組合BCD數(shù)的調(diào)整指令,也有分離BCD數(shù)的調(diào)整指令。另外,BCD碼的加減運算,也可以在運算前由程序先變換成二進制數(shù),然后由計算機對二進制數(shù)運算處理,運算以后再將二進制數(shù)結(jié)果由程序轉(zhuǎn)換為BCD碼。