申明：Blog上的文章只是個人學(xué)習(xí)的一些記錄和總結(jié)，這些記錄部分來自于網(wǎng)絡(luò)，加上自己的一些理解，有些已經(jīng)找不到最原始的出處了，在此對大牛們的貢獻表示感謝，如有侵權(quán)的地方，請通知我，我會盡快刪除。
對關(guān)注性能的程序開發(fā)人員而言，一個好的計時部件既是益友，也是良師。計時器既可以作為程序組件幫助程序員精確的控制程序進程，又是一件有力的調(diào)試武器，在有經(jīng)驗的程序員手里可以盡快的確定程序的性能瓶頸，或者對不同的算法作出有說服力的性能比較。GPU程序性能瓶頸測試，比較常用的工具是NVIDIA PerfHUD ，它能準確測量出渲染管線的每個階段消耗的時間，從時間軸上可以很明顯的看出在渲染一幀是，渲染瓶頸在哪個階段，從而根據(jù)具體情況進行優(yōu)化。CPU程序性能分析工具，Intel公司的 VTune在業(yè)界比較常用，一直想用，還沒試過。
然而下面將要介紹的，從網(wǎng)上搜集到的一些關(guān)于程序代碼段時間統(tǒng)計函數(shù)，用于單個算法的性能分析，比上面提及的工具，更加方便，輕量，易用，根據(jù)你對時間統(tǒng)計的精度要求，選擇不同的時間統(tǒng)計函數(shù)。
1.C語言時間庫<time.h>的clock()函數(shù)
unsigned long sTime,eTime;
double dTime;
sTime = click();
/**////TODOeTime = click();
dTime = (double)(eTime-sTime)/CLOCKS_PER_SEC;
2. RDTSC :(Read Time Stamp Counter)
[1]在Intel Pentium以上級別的CPU中，有一個稱為“時間戳（Time Stamp）”的部件，它以64位無符號整型數(shù)的格式，記錄了自CPU上電以來所經(jīng)過的時鐘周期數(shù)。由于目前的CPU主頻都非常高(1GHz = 10
9)，因此這個部件可以達到納秒級(
一秒的10億分之一，即等于10的負9次方秒)的計時精度。這個精確性是上述方法所無法比擬的。在Pentium以上的CPU中，提供了一條機器指令RDTSC（Read Time Stamp Counter）來讀取這個時間戳的數(shù)字，并將其保存在EDX:EAX寄存器對中。由于EDX:EAX寄存器對恰好是Win32平臺下C++語言保存函數(shù)返回值的寄存器，所以我們可以把這條指令，嵌入?yún)R編代碼的方式，看成是一個普通的函數(shù)調(diào)用。像這樣：
inline unsigned __int64 GetCycleCount()
{
__asm RDTSC
}
但是不行，因為RDTSC不被C++的內(nèi)嵌匯編器直接支持，所以我們要用_emit偽指令直接嵌入該指令的機器碼形式0X0F、0X31，如下：
inline unsigned __int64 GetCycleCount()
{
__asm _emit 0x0F
__asm _emit 0x31
}
以后在需要計數(shù)器的場合，可以調(diào)用兩次GetCycleCount函數(shù)，比較兩個返回值的差，像這樣：
#include <iostream>
#include <Windows.h>
using namespace std;
inline unsigned __int64 GetCycleCount()
{
__asm _emit 0x0F
__asm _emit 0x31
}
int main()
{
unsigned long t;
t = (unsigned long)GetCycleCount();
Sleep(1000);
t = (unsigned long)GetCycleCount() - t;
cout<<"時間："<<t<<endl;
system("pause");
return 0;
}
我的CPU是2.0GHz
所以輸出結(jié)果：
時間：1995027270
程序所花時間秒數(shù) = RDTSC讀出的周期數(shù)T1-RDTSC讀出周期數(shù)T2 / CPU主頻速率（Hz）
缺點：
1.數(shù)據(jù)抖動比較厲害，每次測得結(jié)果都不一樣，波動幅度上百甚至上千
2.在多核下不準確或不可用，有以下幾個方面的原因
[2]：
a.兩個CPU核的內(nèi)部計數(shù)器不同步。如果程序兩次讀取這個計數(shù)器的時候恰好被輪換到不同的核上，那么用來計時就會有比較大的誤差。
b.CPU 的時鐘頻率可能變化，例如筆記本電腦的節(jié)能功能；
c.亂序執(zhí)行導(dǎo)致 RDTSC 測得的周期數(shù)不準，這個問題從 Pentium Pro 時代就存在。
解決方法
[3]：可以采用設(shè)定線程親核性的方法。函數(shù)SetThreadAffinityMask可以指定某線程只在某些核上運行（由第二個參數(shù)設(shè)定，每個位代表一個核）。例如，在需要調(diào)用RDTSC的那個線程里執(zhí)行SetThreadAffinityMask(GetCurrentThread(), 0x00000001);就能保證該線程只在第一個核上運行，不會因為兩個核的RDTSC計數(shù)器不同步而造成計時誤差。我在windows7和VS2005下測試，測出的數(shù)據(jù)和我CPU主頻不符，我一度懷疑剛買的筆記本是不是被刷屏了，后來還找了其他的一些測CPU的工具，比如CPU-Z，這個問題還沒解決。
3.使用QueryPerformanceCounter查詢函數(shù)方法
這個方法在多核下照常有效，QueryPerformanceFrequency()參數(shù)只和主板上的高精度定時器的晶振頻率相關(guān)
在面的例子是兩種求平方根的算法的性能比較，一種采用庫函數(shù)的sqrt(),另一種方法是《編程珠璣》上介紹的牛頓迭代法求平方根，原理類似于二分查找，但是牛頓迭代法收斂速度相比快很多。
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
//a待輸入的開平方根數(shù)
//x 選取的x0點
//y 每次迭代的中間值
double a, x,y;
unsigned long start,endt;
cin>>a;
LARGE_INTEGER t1,t2,tc;
QueryPerformanceFrequency(&tc);
printf("Frequency:%u\n",tc.QuadPart);
QueryPerformanceCounter(&t1);
if (a<0)
cout<<"負數(shù)沒有平方根！"<<endl;
else
{
x = 1;
y = (x+a/x)/2;
while (x!=y)
{
x = y;
y = (x+a/x)/2;
}
}
QueryPerformanceCounter(&t2);
//牛頓迭代法求平方根所需時間;
printf("Lasting Time:%u\n",(t2.QuadPart-t1.QuadPart));
//duration = (double)(finish - start)/CLOCKS_PER_SEC ;
cout <<a<<"的平方根為："<<x<<endl;
QueryPerformanceCounter(&t1);
sqrt(a);
QueryPerformanceCounter(&t2);
//math.h庫函數(shù)sqrt求平方根所需時間;
printf("Lasting Time:%u\n",(t2.QuadPart-t1.QuadPart));
cout<<a<<"的平方根為："<<sqrt(a)<<endl;
system("pause");
return 0;
兩種求平方根所需時間對比如下：
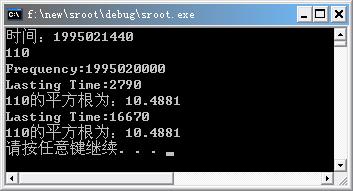
在圖形學(xué)中求平方根使用頻率非常高，尤其是在碰觸檢測中，盡量提高求平方根的效率是非常有必要的。
總結(jié)：效率就是生命，在平時的項目開發(fā)中盡量做到簡單，簡單代表高效。這是檢測高效的第一步。
引用：
[1]:http://zhidao.baidu.com/question/41853032.html
[2]:http://blog.csdn.net/Solstice/archive/2010/01/16/5196544.aspx
[3]:http://blog.21ic.com/user1/5184/archives/2009/65439.html