Sunshine Alike

一、 MFC 框架下使用 OpenGL 繪圖演示平移、旋轉、縮放等操作的具體實現

二、 實現算法

繪制的圖形以各種頂點及頂點之間的線、面構成

要想對這些圖形進行操作，只需要對各種頂點在坐標系中的坐標進行轉換即可

頂點在 OpenGL 中的坐標以四維形式表示：（ X,Y,Z,W ）

其中 X,Y,Z 對應三維系統中 X ， Y ， Z 三個柚； W 默認為 1 ，一般為了方便各種操作時坐標換算而將三維坐標系提升為四次，即齊次坐標系。

① 平移操作——對應 glTranslate 函數：

初始點：（ X,Y,Z,W ）

使用轉換矩陣 TMatrix ：

1, 0, 0, Tx

0, 1, 0, Ty

0, 0, 1, Tz

0, 0, 0, 1

(X’, Y’, Z’) = TMatrix * (X, Y, Z), 其中 Tx ， Ty ， Tz 對應 glTranslate 函數中的三個參數，分別表示三個方向的的平移量；原始坐標右乘平移矩陣后即得到新的坐標

③ 縮放操作——對應 glScale 函數：

使用轉換矩陣為 SMatrix ：

Sx, 0, 0, 0

0, Sy, 0, 0

0, 0, Sz, 0

0, 0, 0, 1

(X’, Y’, Z’) = SMatrix * (X, Y, Z)

此次自己實現的縮放函數與 OpenGL 有所不同，我實現的是與圖形的中心點為基準進行縮放，所以進行矩陣變換前需要計算各個坐標的位置并求幾何中心。

② 旋轉操作——對應 glRotate 函數（逆時針方向）：

在三維坐標系統中，旋轉操作與二維情況有所不同，因為三維中的一個點可以繞不同的方向進行旋轉，所以除了要指定旋轉角度外，還要指定旋轉軸

當所取旋轉軸為 X ， Y 或 Z 三個坐標軸時，與二維情況相似

即所選取的軸那一方向上的坐標不變，在其它兩個軸所成的平面上進行二維旋轉變換

根據這個規律可以把三維中繞任意軸旋轉的操作分為幾個操作來完成

步驟：

先將待旋轉的坐標與旋轉軸平移，使旋轉軸經過原點

進行若干次旋轉操作，例旋轉軸與 Z 軸正向重合

依據對坐標軸旋轉的方法將待旋轉坐標進行旋轉操作

應用逆旋轉使旋轉軸回到原方向

應用逆平移使旋轉軸回到原位置

 

二維情況下旋轉矩陣為：

cosQ, -sinQ, 0

sinQ, cosQ, 0

0, 0, 1

 

此次采用先繞 X 轉做旋轉 Rx ，再繞 Y 轉旋轉 Ry 使旋轉軸與 Z 轉正向重合，再繞 Z 軸做 Rz 旋轉 Q 度，再進行逆操作還原位置

即 : (X’, Y’, Z’) = Rx*Ry*Rz(Q)*(Ry ^-1 )*(Rx^-1)

其中 Q 是需要旋轉的角度， 逆矩陣 A ^-1 = A*/|A|

代數余子式： (-1)^(i+j)Aij

 

三、 程序結構

使用 MFC 生成程序界面， OpenGL 負責繪制圖形

文檔 / 視圖結構

文件數據為，圖形的類型以及各個頂點坐標

從菜單中選擇要進行的操作：平移，旋轉，縮放后出現對話框輸入參數

平移—— 3 個參數，分別表示 X,Y,Z 各個軸向的平移量

旋轉—— 4 個參數，第一個角度 Angle, 后三個表示轉軸向量

縮放—— 3 個參數，表示 X,Y,Z 軸方向上的縮放比例，可以為負數

文件數據為：

一個 CArray<Point, Point> m_PointArray 保存圖形的各個頂點信息

一個表示圖形形狀的 int m_nShape 表示 glBegin 函數里的參數

 

四、 MFC 中使用 OpenGL 繪圖

具體還沒有研究，只是照搬網上教程，以后補上

View 頭文件中加入

       HGLRC m_hRC;    //Rendering Context

       CDC* m_pDC;        //Device Context

       BOOL InitializeOpenGL();    //Initialize OpenGL

BOOL SetupPixelFormat();    //Set up the Pixel Format

 

實現部分：

此外需要將 View 類中的 OnEraseBkgnd 消息屏蔽掉，使之直接返回 TRUE ，因為消除背景的工作已經將由 OpenGL 來做，不需要由這個函數再來做一遍。

在 PreCreateWindow 函數中修改

cs.style |= WS_CLIPSIBLINGS | WS_CLIPCHILDREN;

保證 OpenGL 不會繪制到其它窗口中去

在 OnCreate 函數中調用 InitializeOpenGL 函數就可以在 View 中進行繪制了

 

另外，為了適應窗口大小變化，還需要在 OnSize 函數中加入高速視域的代碼

 

做好一切準備工作后，就可以在 OnDraw 中使用 OpenGL 函數進行繪制了，不過別忘了程序最后要進行資源的釋放，在 OnDestroy 中加入清理工作

      最后程序演示結果：

 

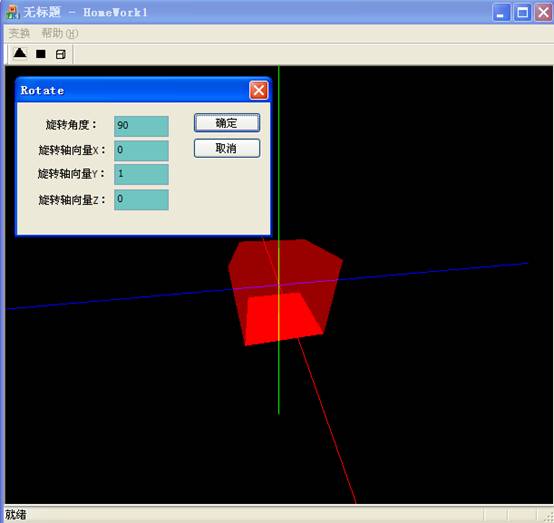
五、 編程中遇到的問題總結

1.       復習了操作符重載的相關內容

2.       浮點數的比較，這個比較重要，以前在課上只是聽說，沒有特別印象，在耗費了我 2 個小時的調試之后，以后應該再也不會忘了。 Fabs （ f1-f2 ） <= 精度要求

3.       此次寫的工具類 Matrix 勝于處理向量，矩陣的相關操作，因為偷懶還不太完善，尤其是矩陣的一些操作比較求模，求逆都沒有實現，以后補上

http://www.shnenglu.com/Files/sunshinealike/HomeWork1.rar