??1?/*?
??2??*?SOUR:zju2589
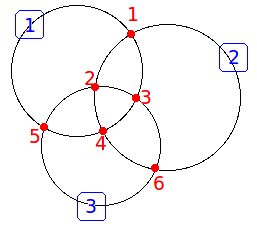
??3??*?ALGO:computational?geomtry?計(jì)算平面上不重合的n個(gè)圓形成的區(qū)域
??4??*?基本的方法，如圖所示，將所有圓之間的交點(diǎn)作為點(diǎn)，將在同一個(gè)圓上的所有交點(diǎn)之間的弧作
??5??*?為邊建立一張有向圖，之后可以利用平面圖的歐拉定理
??6??*???????????V?-?E?+?F?=?2
??7??*?由于V已知，E已知，F(xiàn)就可以求出來(lái)了。
??8??*?由于歐拉定理是對(duì)一張無(wú)向連通圖成立的，如果圖有多個(gè)連通塊的時(shí)候需要對(duì)歐拉定理做一些
??9??*?修改。由于多個(gè)有向圖的面共享最外邊的面，所以設(shè)聯(lián)通塊的個(gè)數(shù)為n
?10??*?V?-?E?+?F?=?2?*?n?,?但是需要減去n個(gè)聯(lián)通塊共享的最大平面
?11??*?所以?F?=?n?+?1?+?E?-?V;
?12??*?DATE:?2010年?07月?08日?星期四?14:49:41?CST
?13??*?COMM:5
?14??*?*/
?15?const?int?N?=?64;
?16?const?double?eps?=?1e-8;
?17?int?n,?vis[N],?g[N][N];
?18?double?r[N];
?19?struct?point_t?{
?20?????double?x,?y;
?21?????point_t(){}
?22?????point_t(double?a,?double?b){x?=?a,?y?=?b;}?
?23?}c[N];
?24?
?25?int?dcmp(double?x)?{?return?(x?>?eps)?-?(x?<?-eps);}?
?26?bool?operator?<?(point_t?a,point_t?b)?
?27?{
?28???if?(dcmp(a.x?-?b.x))?{
?29???????return?a.x?<?b.x;
?30???}
?31???return?dcmp(a.y?-?b.y)?<?0;
?32?}
?33?
?34?point_t?operator?+?(point_t?a,?point_t?b)?{?return?point_t(a.x+b.x,?a.y+b.y);}
?35?point_t?operator?-?(point_t?a,?point_t?b)?{?return?point_t(a.x-b.x,?a.y-b.y);}
?36?double?dist(point_t?a,?point_t?b)?{?return?hypot(a.x-b.x,?a.y-b.y);}
?37?double?sqr(double?x)?{?return?x?*?x;}
?38?point_t?normal(point_t?a)?{?return?point_t(a.x?/?hypot(a.x,?a.y),?a.y?/?hypot(a.x,?a.y));}
?39?point_t?scale(point_t?a,?double?fac)?{?return?point_t(a.x?*?fac,?a.y?*?fac);}
?40?bool?intersect(point_t?c1,?double?r1,?point_t?c2,?double?r2,?point_t?&a,?point_t?&b)
?41?{
?42???double?d?=?dist(c1,?c2);
?43???if?(d?<?fabs(r1?-?r2)?-?eps?||?d?>?r1?+?r2?+?eps)?{
?44???????return?false;
?45???}
?46???double?len?=?(sqr(r1)?-?sqr(r2)?+?sqr(d))?/?2.0?/?d;
?47???double?h?=?sqrt(sqr(r1)?-?sqr(len));
?48???point_t?t?=?normal(c2?-?c1);
?49???point_t?p?=?c1?+?scale(t,?len);
?50???point_t?v?=?scale(point_t(-t.y,?t.x),?h);
?51???a?=?p?+?v,?b?=?p?-v;
?52???return?true;
?53?}
?54?
?55?void?init()
?56?{
?57???int?i;
?58???memset(g,?0,?sizeof(g));
?59???memset(vis,?0,?sizeof(vis));
?60???for?(i?=?0;i?<?n;i++)?{
?61???????g[i][i]?=?1;
?62???}
?63?}
?64?
?65?int?main()
?66?{
?67???int?testcase,?i,?j,?k;
?68???scanf("%d",?&testcase);
?69???while?(testcase--)?{
?70???????scanf("%d",?&n);
?71???????set?<point_t>?allpoint,?p[64];
?72???????for?(i?=?0;i?<?n;i++)?{
?73???????????scanf("%lf?%lf?%lf",?&c[i].x,?&c[i].y,?&r[i]);
?74???????}
?75???????init();
?76???????for?(i?=?0;i?<?n;i++)?{
?77???????????for?(j?=?i?+?1;j?<?n;j++)?{
?78???????????????point_t?a,?b;
?79???????????????if?(intersect(c[i],?r[i],?c[j],?r[j],?a,?b))?{
?80???????????????????allpoint.insert(a),?allpoint.insert(b);
?81???????????????????p[i].insert(a),?p[i].insert(b);
?82???????????????????p[j].insert(a),?p[j].insert(b);
?83???????????????????g[i][j]?=?g[j][i]?=?1;
?84???????????????}
?85???????????}
?86???????}
?87???????for?(k?=?0;k?<?n;k++)?{
?88???????????for?(i?=?0;i?<?n;i++)?{
?89???????????????for?(j?=?0;j?<?n;j++)?{
?90???????????????????g[i][j]?|=?g[i][k]?&?g[k][j];
?91???????????????}
?92???????????}
?93???????}
?94???????int?f?=?1;
?95???????for?(i?=?0;i?<?n;i++)?{
?96???????????f?+=?p[i].size();
?97???????????if?(!vis[i])?{
?98???????????????f?+=?1;
?99???????????????for?(j?=?0;j?<?n;j++)?{
100???????????????????vis[j]?|=?g[i][j];
101???????????????}
102???????????}
103???????}
104???????f?-=?allpoint.size();
105???????printf("%d\n",?f);
106???}?
107???return?0;
108?}
109?
110?