schindlerlee原創(chuàng),禁止轉載和用于商業(yè)用途
題目描述:
給定一個矩陣,找一個起始點,由該點開始不斷馬跳,要求跳到的后一節(jié)點比前一節(jié)點的值大,問最多可以跳多少步,并且輸出跳躍的序列,如果兩個跳躍序列步數(shù)相同,給出字典序較小的
1 2 4
1 2 3
兩個序列當然是后一個較小
第一感覺可以求出每個節(jié)點的跳躍序列,比較長度得出結果。但是我們發(fā)現(xiàn)其中有很多重復的路徑,由此想到dp。
本來此題如果只要求最長的跳躍步數(shù)的話,就是一道比較簡單的dp了。但是題目要求輸出最小的序列,需要稍微復雜一點的處理。
可以考慮為每個點增加一個pre坐標,指向前一個點,但是這就帶來一個問題,要尋找最小的序列,如果有兩個相同長度的序列可供當前點選擇的話,直接貪心是錯誤的,下圖為反例
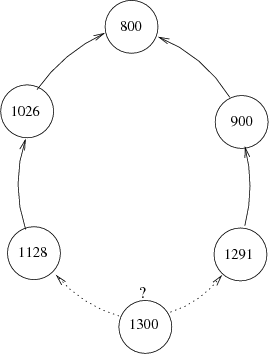
可以發(fā)現(xiàn),如果只比較前一點的話,左邊的路線是正確的,但是實際上右邊的是正確的。注意這一點基本就沒問題了。
1 /*
2 * SOUR:pku 2111
3 * ALGO:dp or search
4 * DATE: 2009年 08月 29日 星期六 04:16:26 CST
5 * COMM:
6 * */
7 #include<iostream>
8 #include<cstdio>
9 #include<cstdlib>
10 #include<cstring>
11 #include<algorithm>
12 using namespace std;
13 const int maxint = 0x7fffffff;
14 const long long max64 = 0x7fffffffffffffffll;
15 #define debug 1
16 const int N = 410;
17 int mov[8][2] = { {1, 2}, {2, 1}, {-1, 2}, {2, -1}, //
18 {1, -2}, {-2, 1}, {-1, -2}, {-2, -1}
19 };
20
21 int g[N][N], pre[N][N][2], n, dp[N][N], out[N], on;
22 struct L {
23 int x, y;
24 int val;
25 } query[N * N];
26 bool operator <(L a, L b)
27 {
28 return a.val < b.val;
29 }
30 int a[N*N],b[N*N];
31 bool judge(int tx,int ty,int px,int py)
32 {
33 int sp = 0,ta,tb,i;
34 while(tx != -1) {
35 a[sp] = g[tx][ty];
36 b[sp] = g[px][py];
37 sp ++;
38 ta = pre[tx][ty][0];
39 tb = pre[tx][ty][1];
40 tx = ta,ty = tb;
41
42 ta = pre[px][py][0];
43 tb = pre[px][py][1];
44 px = ta,py = tb;
45 }
46 for(i = sp - 1;i >= 0 && a[i] == b[i];i--);
47 if(a[i] < b[i])
48 return true;
49 return false;
50 }
51
52 int main()
53 {
54 int i, j, k, x, y, big, tx, ty;
55 scanf("%d", &n);
56 for (i = 0; i < n; i++) {
57 for (j = 0; j < n; j++) {
58 scanf("%d", &g[i][j]);
59 query[i * n + j].val = g[i][j];
60 query[i * n + j].x = i;
61 query[i * n + j].y = j;
62 pre[i][j][0] = pre[i][j][1] = -1;
63 }
64 }
65
66 sort(query, query + n * n);
67 for (i = 0; i < n * n; i++) {
68 x = query[i].x;
69 y = query[i].y;
70 for (j = 0; j < 8; j++) {
71 int tx = x + mov[j][0];
72 int ty = y + mov[j][1];
73 if (tx >= 0 && tx < n && ty >= 0 && ty < n
74 && g[x][y] > g[tx][ty]) {
75 if (dp[x][y] < dp[tx][ty] + 1) {
76 dp[x][y] = dp[tx][ty] + 1;
77 pre[x][y][0] = tx;
78 pre[x][y][1] = ty;
79 } else if (dp[x][y] == dp[tx][ty] + 1) {
80 int px = pre[x][y][0];
81 int py = pre[x][y][1];
82 if (judge(tx,ty,px,py)) {
83 pre[x][y][0] = tx;
84 pre[x][y][1] = ty;
85 }
86 }
87 }
88 }
89 }
90 on = 0, big = 0;
91 for (i = 0; i < n; i++) {
92 for (j = 0; j < n; j++) {
93 if (dp[i][j] > big) {
94 big = dp[i][j];
95 x = i, y = j;
96 }
97 }
98 }
99 while (x != -1 && y != -1) {
100 out[on++] = g[x][y];
101 tx = pre[x][y][0];
102 ty = pre[x][y][1];
103 x = tx, y = ty;
104 }
105 printf("%d\n", on);
106 for (i = on - 1; i >= 0; i--) {
107 printf("%d\n", out[i]);
108 }
109 return 0;
110 }
111