【定理】設(shè)N為Blum數(shù),N ∤ d,若同余方程x2≡d (mod N)有解,則d的平方根中有一半的Jacobi符號為1,另一半Jacobi符號為-1;且僅有一個平方根為模N的二次剩余
證明:

【推論】設(shè)N為Blum數(shù),N=P×Q,令
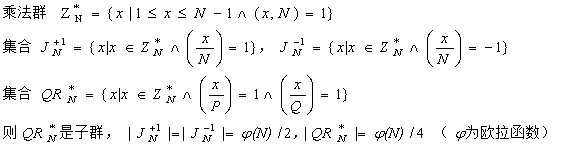
證明:
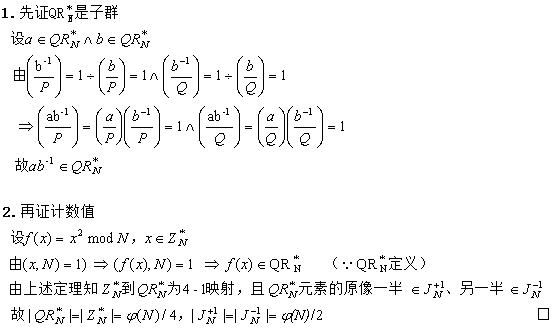
【例子】由定義知N=21=3×7為Blum數(shù),則相關(guān)乘法群、二次剩余子群、Jacobi集合如下

【應(yīng)用一】Blum-Goldwasser公鑰加密

解密正確性是因為步驟1用到了歐拉定理及求平方根的如下算法,步驟2用到了中國剩余定理

從上可得x=s(P+1)/4 mod P或x=P-s(P+1)/4 mod P,因(-1)(P-1)/2等于-1 mod P,故前者為模P的二次剩余。從加密流程可知{s1,s2,...,sn+1}正是模N二次剩余類的子集。
所以從密文中r=sn+1求它的(p+1)/4次冪、(q+1)/4次冪,迭代n次就得到了s1模p的解、s1模q的解,又因p、q、n在迭代中不變,故用歐拉定理預(yù)計算dp mod (p-1)、dq mod (q-1)。
另一種(不太高效而直接的)解密如下
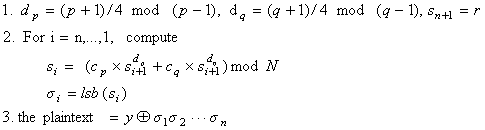
另加密與明文異或的那部分實際是偽隨機(jī)比特發(fā)生器,因為平方模N構(gòu)成二次剩余類上的單向陷門置換,其最低有效位是核心斷言,故從si+1求出lsb(si)是不可行的。簡單證明如下

由于均勻選擇一個種子s0,所以為概率加密,進(jìn)而由可證明安全定理(每個概率公鑰加密都是多項式安全的,及每個多項式安全的公鑰加密都是語義安全的)知滿足IND-CPA安全性
易知IND-CCA2安全性是不滿足的,因為敵手可用如下攻擊方法獲取明文:已知目標(biāo)密文C=(r, m⊕σ1σ2⋯σn),構(gòu)造新密文C’=(r, m’⊕m⊕σ1σ2⋯σn),將C’發(fā)給解密預(yù)言機(jī)得到m’’,則m=m’’⊕m’。
由于加密產(chǎn)生的r與σ1σ2⋯σn都是偽隨機(jī)的,所以密文(r, x⊕σ1σ2⋯σn)的分布是偽隨機(jī)的,在目標(biāo)密文前的解密詢問會得到若干密文與明文對,無論怎么構(gòu)造一對明文,任選其一加密得到的密文都不可區(qū)分。因此IND-CCA1安全性是滿足的
【應(yīng)用二】無爪函數(shù)/置換構(gòu)造


如上構(gòu)造用到Blum數(shù)的上述推論,及基于大整數(shù)因子分解的困難假設(shè)。這里主要解釋下為什么由兩個Jacobi符號不同的平方根可計算大整數(shù)的素因子
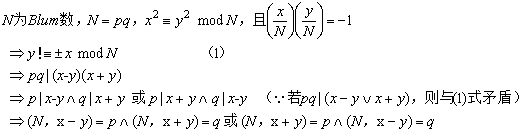
【應(yīng)用三】偽隨機(jī)數(shù)發(fā)生器
Xn+1=Xn2 mod N n=0、1、2...,X0為種子
顯然種子不為1。若為一個非二次剩余,則從X1開始就為二次剩余子群的元素,但最后必回到X1而非X0;若為二次剩余,則為了安全需要考究隨機(jī)數(shù)數(shù)列的周期是否整周期(二次剩余子群的大小減1)。
下面具體分析周期。先舉例幾個很小的Blum數(shù)

從上面例子可以發(fā)現(xiàn),由二次剩余子群構(gòu)成的隨機(jī)數(shù)數(shù)列不一定是整周期的,對于N=33無論種子怎么選,都是整周期4;對于N=57若種子選-8或7則周期為2,選其它則為6。
現(xiàn)在一般化考慮,什么情況下才產(chǎn)生整周期?論證如下




