經典的復雜性關系
P是多項式時間確定型圖靈機可識別的語言類，NP是多項式時間
非確定型圖靈機可識別的語言類，NPC表示NP完全問題類，coNP表示NP的補，coNPC表示NPC的補。確定型圖靈機是一種從不選擇移動的特殊的非確定型圖靈機，故自然有P屬于NP
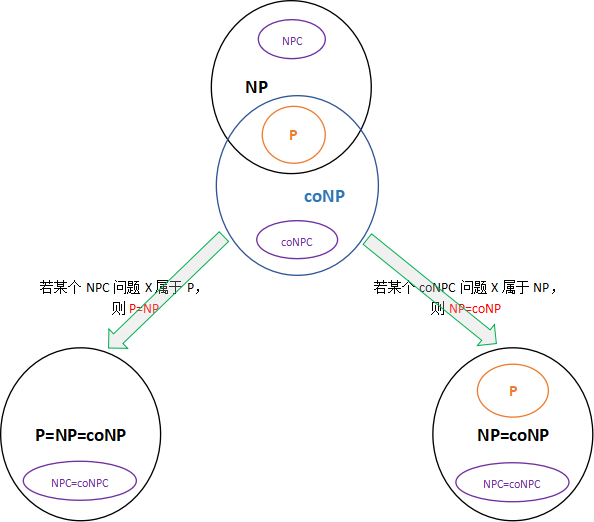coNP、coNPC的定義之集合表述
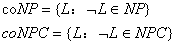
上面頂部的圖有個假設前提是：
coNPC不屬于NP，即我們相信NP完全問題的補都不屬于NP。但
當P=NP或NP=coNP時，可以發現coNPC屬于NP
◆ 為什么coNPC屬于coNP？
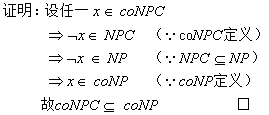
◆ 為什么NPC 不屬于coNP？
◆ 為什么P屬于coNP?
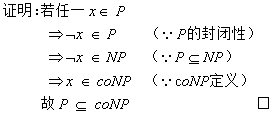◆ 當P=NP時，為什么NP=coNP？
◆ 當NP=coNP時，為什么NPC=coNPC？
前文的關系演變圖沒考慮多項式空間問題類PS與遞歸問題類（因為那兩個條件不會影響到它們），
PS（NPS）是帶多項式空間限制的確定型（非確定型）圖靈機可接受的語言類，但不限制運行時間可能需超多項式或指數時間，在外圍加上PS與遞歸語言類后如下
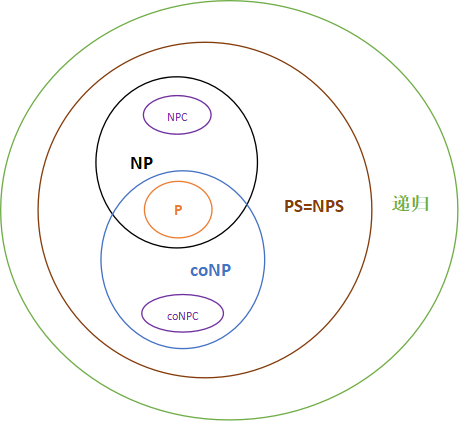
◆ 為什么coNP 屬于PS？
用于分析加密
無論對稱還是公鑰加密，統一設加密運算為E，解密為D。對于正常用戶，E和D皆為DTM（確定性圖靈機）；對于敵手，若攻擊對稱加密，則E和D為NTM（非確定性圖靈機），攻擊公鑰則解密為NTM。由于E和D輸入為密鑰和明文或密文，因此DTM和NTM可采用多道/多帶結構。DTM代表P類計算，NTM代表NP類計算，故對于公鑰加密安全保障要求
P!=NP，這是一個
必要條件。另根據計算理論定理，必有L(NTM)=L(DTM)，但是它對應的DTM可能要多花費指數時間，這亦說明破解公鑰的解密是困難的
零知識復雜性關系
依據Oded Goldreich的《密碼學基礎》，關系如下
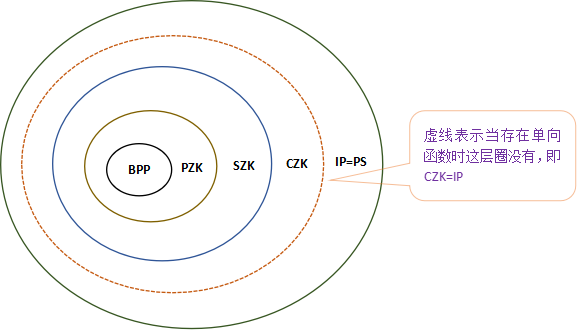
相關原文片段引用如下
BPP是可被概率多項式時間圖靈機(即隨機化算法)識別的語言類，IP是所有具有交互證明系統的語言構成的類，等于多項式空間語言類即前文經典復雜性關系中的PS，如下圖所述
SZK!=CZK是因為計算不可分辨不一定能推出統計不可分辨，
BPP!=PZK之原因可理解為BPP是退化的特殊的完備交互證明系統（證明者什么都不做，僅由驗證者概率性地決定是否接受或拒絕）。
當（非均勻）單向函數存在時
CZK=IP，涉及的命題與定理如下
也就是說PS類中的每種語言都具有零知識證明系統，比如NP有如下構造
posted on 2024-02-09 22:19
春秋十二月 閱讀(1321)
評論(0) 編輯 收藏 引用 所屬分類:
Compute Theory