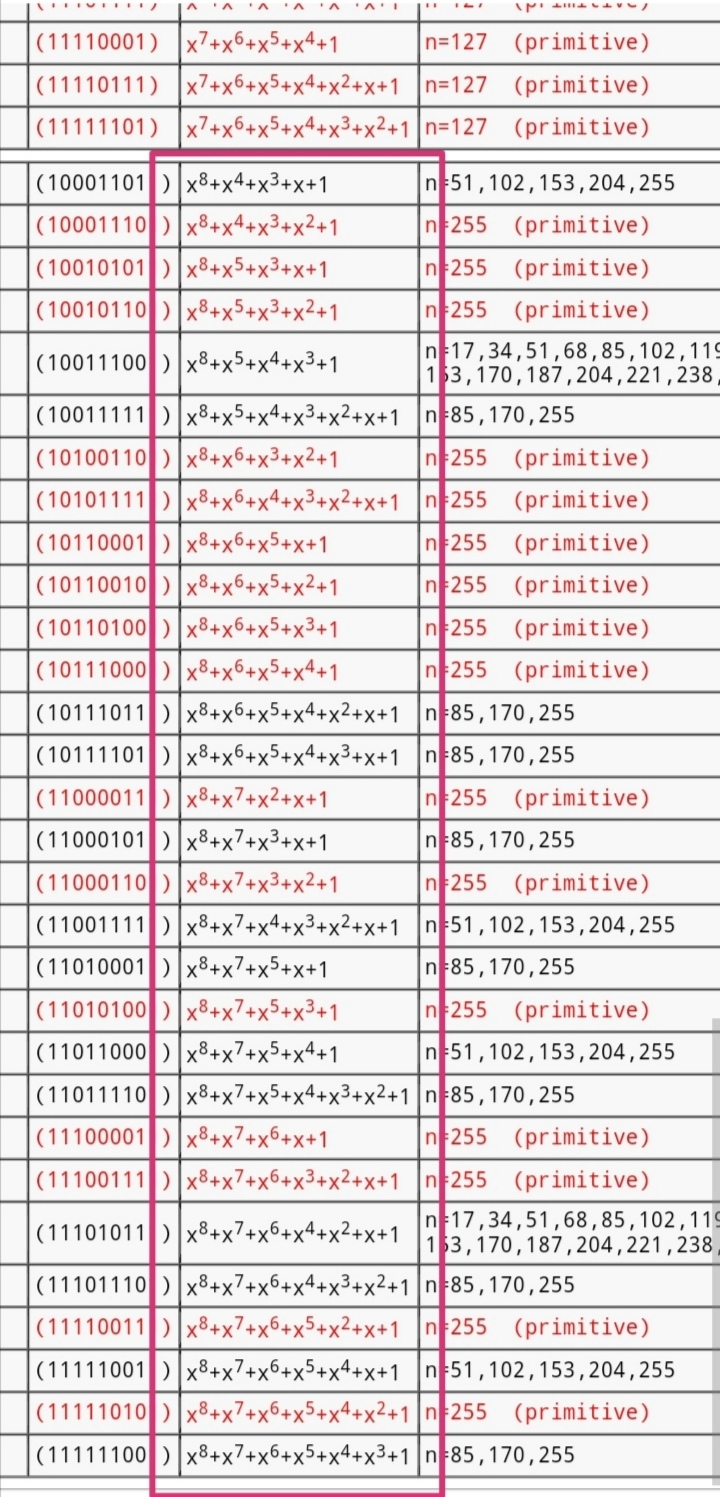
有理數(shù)域的本原多項(xiàng)式與有限域的本原多項(xiàng)式定義不同，前者不要求不可約（由高斯引理知兩個(gè)本原多項(xiàng)式的乘積還是本原），后者則必須不可約（確保生成的有限域其每個(gè)元素有逆元）。aes基于有限域F{0,1}設(shè)計(jì)，故使用的模8次多項(xiàng)式不可約
P(x)=x^8+x^4+x^3+x+1，但不是本原多項(xiàng)式，因?yàn)樗碾A是51而非255。有限域次數(shù)為8的本原多項(xiàng)式有16個(gè)、不可約多項(xiàng)式有30個(gè)（由莫比烏斯反演推出），具體多項(xiàng)式影響s盒與列混合操作的實(shí)現(xiàn)。不可約加之0的逆元規(guī)定為0，保證正確加解密。若0的逆元規(guī)定為非0比如x，則導(dǎo)致x有兩個(gè)逆元，便違反了逆元唯一性，除非s盒不用有限域設(shè)計(jì)。逆元等于其自身的非0元素只有1，原因可類比模素?cái)?shù)二次剩余的求解
posted on 2023-09-13 02:00
春秋十二月 閱讀(390)
評(píng)論(0) 編輯 收藏 引用 所屬分類:
Algorithm