Floyd-Warshall算法DP流程詳解
Floyd-Warshall算法,簡稱Floyd算法,用于求解任意兩點間的最短距離,時間復雜度為O(n^3)。我們平時所見的Floyd算法的一般形式如下:2 int i,j,k;
3 for(k=1;k<=n;k++)
4 for(i=1;i<=n;i++)
5 for(j=1;j<=n;j++)
6 if(dist[i][k]+dist[k][j]<dist[i][j])
7 dist[i][j]=dist[i][k]+dist[k][j];
8 }
注意下第6行這個地方,如果dist[i][k]或者dist[k][j]不存在,程序中用一個很大的數(shù)代替。最好寫成if(dist[i][k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]<dist[i][j]),從而防止溢出所造成的錯誤。
上面這個形式的算法其實是Floyd算法的精簡版,而真正的Floyd算法是一種基于DP(Dynamic Programming)的最短路徑算法。
設(shè)圖G中n 個頂點的編號為1到n。令c [i, j, k]表示從i 到j(luò) 的最短路徑的長度,其中k 表示該路徑中的最大頂點,也就是說c[i,j,k]這條最短路徑所通過的中間頂點最大不超過k。因此,如果G中包含邊<i, j>,則c[i, j, 0] =邊<i, j> 的長度;若i= j ,則c[i,j,0]=0;如果G中不包含邊<i, j>,則c (i, j, 0)= +∞。c[i, j, n] 則是從i 到j(luò) 的最短路徑的長度。
對于任意的k>0,通過分析可以得到:中間頂點不超過k 的i 到j(luò) 的最短路徑有兩種可能:該路徑含或不含中間頂點k。若不含,則該路徑長度應(yīng)為c[i, j, k-1],否則長度為 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取兩者中的最小值。
狀態(tài)轉(zhuǎn)移方程:c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]},k>0。
這樣,問題便具有了最優(yōu)子結(jié)構(gòu)性質(zhì),可以用動態(tài)規(guī)劃方法來求解。
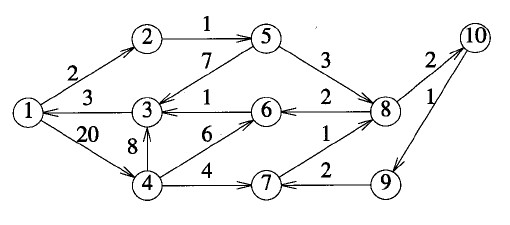
下面通過程序來分析這一DP過程,對應(yīng)上面給出的有向圖:
2 using namespace std;
3
4 const int INF = 100000;
5 int n=10,map[11][11],dist[11][11][11];
6 void init(){
7 int i,j;
8 for(i=1;i<=n;i++)
9 for(j=1;j<=n;j++)
10 map[i][j]=(i==j)?0:INF;
11 map[1][2]=2,map[1][4]=20,map[2][5]=1;
12 map[3][1]=3,map[4][3]=8,map[4][6]=6;
13 map[4][7]=4,map[5][3]=7,map[5][8]=3;
14 map[6][3]=1,map[7][8]=1,map[8][6]=2;
15 map[8][10]=2,map[9][7]=2,map[10][9]=1;
16 }
17 void floyd_dp(){
18 int i,j,k;
19 for(i=1;i<=n;i++)
20 for(j=1;j<=n;j++)
21 dist[i][j][0]=map[i][j];
22 for(k=1;k<=n;k++)
23 for(i=1;i<=n;i++)
24 for(j=1;j<=n;j++){
25 dist[i][j][k]=dist[i][j][k-1];
26 if(dist[i][k][k-1]+dist[k][j][k-1]<dist[i][j][k])
27 dist[i][j][k]=dist[i][k][k-1]+dist[k][j][k-1];
28 }
29 }
30 int main(){
31 int k,u,v;
32 init();
33 floyd_dp();
34 while(cin>>u>>v,u||v){
35 for(k=0;k<=n;k++){
36 if(dist[u][v][k]==INF) cout<<"+∞"<<endl;
37 else cout<<dist[u][v][k]<<endl;
38 }
39 }
40 return 0;
41 }
輸入 1 3
輸出 +∞
+∞
+∞
+∞
28
10
10
10
9
9
9
Floyd-Warshall算法不僅能求出任意2點間的最短路徑,還可以保存最短路徑上經(jīng)過的節(jié)點。下面用精簡版的Floyd算法實現(xiàn)這一過程,程序中的圖依然對應(yīng)上面的有向圖。
2 using namespace std;
3
4 const int INF = 100000;
5 int n=10,path[11][11],dist[11][11],map[11][11];
6 void init(){
7 int i,j;
8 for(i=1;i<=n;i++)
9 for(j=1;j<=n;j++)
10 map[i][j]=(i==j)?0:INF;
11 map[1][2]=2,map[1][4]=20,map[2][5]=1;
12 map[3][1]=3,map[4][3]=8,map[4][6]=6;
13 map[4][7]=4,map[5][3]=7,map[5][8]=3;
14 map[6][3]=1,map[7][8]=1,map[8][6]=2;
15 map[8][10]=2,map[9][7]=2,map[10][9]=1;
16 }
17 void floyd(){
18 int i,j,k;
19 for(i=1;i<=n;i++)
20 for(j=1;j<=n;j++)
21 dist[i][j]=map[i][j],path[i][j]=0;
22 for(k=1;k<=n;k++)
23 for(i=1;i<=n;i++)
24 for(j=1;j<=n;j++)
25 if(dist[i][k]+dist[k][j]<dist[i][j])
26 dist[i][j]=dist[i][k]+dist[k][j],path[i][j]=k;
27 }
28 void output(int i,int j){
29 if(i==j) return;
30 if(path[i][j]==0) cout<<j<<' ';
31 else{
32 output(i,path[i][j]);
33 output(path[i][j],j);
34 }
35 }
36 int main(){
37 int u,v;
38 init();
39 floyd();
40 while(cin>>u>>v,u||v){
41 if(dist[u][v]==INF) cout<<"No path"<<endl;
42 else{
43 cout<<u<<' ';
44 output(u,v);
45 cout<<endl;
46 }
47 }
48 return 0;
49 }
輸入 1 3
輸出 1 2 5 8 6 3
posted on 2009-04-21 00:38 極限定律 閱讀(8784) 評論(3) 編輯 收藏 引用 所屬分類: ACM/ICPC


