目錄
零、前言
一、引例
1、區(qū)間最值
2、區(qū)間求和
二、線段樹的基本概念
1、二叉搜索樹
2、數(shù)據(jù)域
3、指針表示
4、數(shù)組表示
三、線段樹的基本操作
1、構(gòu)造
2、更新
3、詢問
四、線段樹的經(jīng)典案例
1、區(qū)間最值
2、區(qū)間求和
3、區(qū)間染色
4、矩形面積并
5、區(qū)間K大數(shù)
五、線段樹的常用技巧
1、二維線段樹 - 矩形樹
2、三維線段樹 - 空間樹
七、線段樹相關(guān)題集整理
零、前言
最近工作比較忙，好久沒更新了，只能在過年期間抽時間寫上一篇，美其名曰賀歲版，很享受寫文章的過程，不想就這么斷了連載，但是接下來可能會更忙，雖然很想一直堅持下去，但是臣妾做不到啊……
一、引例
1、區(qū)間最值
【例題1】給定一個n（n <= 100000）個元素的數(shù)組A，有m(m <= 100000)個操作，共兩種操作：
1、Q a b 詢問：表示詢問區(qū)間[a, b]的最大值；
2、C a c 更新：表示將第a個元素變成c；
靜態(tài)的區(qū)間最值可以利用RMQ來解決，但是RMQ的ST算法是在元素值給定的情況下進行的預(yù)處理，然后在O(1)時間內(nèi)進行詢問，這里第二種操作需要實時修改某個元素的值，所以無法進行預(yù)處理。 2、區(qū)間求和
【例題2】給定一個n(n <= 100000)個元素的數(shù)組A，有m(m <= 100000)個操作，共兩種操作：
1、Q a b 詢問：表示詢問區(qū)間[a, b]的元素和；
2、A a b c 更新：表示將區(qū)間[a, b]的每個元素加上一個值c；
先來看樸素算法，兩個操作都用遍歷來完成，單次時間復(fù)雜度在最壞情況下都是O(n)的，所以m次操作下來總的時間復(fù)雜度就是O(nm)了，復(fù)雜度太高。
再來看看樹狀數(shù)組，對于第一類操作，樹狀數(shù)組可以在log(n)的時間內(nèi)出解；然而第二類操作，還是需要遍歷每個元素執(zhí)行add操作，復(fù)雜度為nlog(n)，所以也不可行。這個問題同樣也需要利用區(qū)間拆分的思想。
線段樹就是利用了區(qū)間拆分的思想，完美解決了上述問題。
二、線段樹的基本概念
1、二叉搜索樹
線段樹是一種二叉搜索樹，即每個結(jié)點最多有兩棵子樹的樹結(jié)構(gòu)。通常子樹被稱作“左子樹”（left subtree）和“右子樹”（right subtree）。線段樹的每個結(jié)點存儲了一個區(qū)間（線段），故而得名。
圖二-1-1
如圖二-1-1所示，表示的是一個[1, 6]的區(qū)間的線段樹結(jié)構(gòu)，每個結(jié)點存儲一個區(qū)間（注意這里的存儲區(qū)間并不是指存儲這個區(qū)間里面所有的元素，而是只需要存儲區(qū)間的左右端點即可），所有葉子結(jié)點表示的是單位區(qū)間（即左右端點相等的區(qū)間），所有非葉子結(jié)點（內(nèi)部結(jié)點）都有左右兩棵子樹，對于所有非葉子結(jié)點，它表示的區(qū)間為[l, r]，那么令mid為(l + r)/2的下整，則它的左兒子表示的區(qū)間為[l, mid]，右兒子表示的區(qū)間為[mid+1, r]?；谶@個特性，這種二叉樹的內(nèi)部結(jié)點，一定有兩個兒子結(jié)點，不會存在有左兒子但是沒有右兒子的情況。
基于這種結(jié)構(gòu)，葉子結(jié)點保存一個對應(yīng)原始數(shù)組下標(biāo)的值，由于樹是一個遞歸結(jié)構(gòu)，兩個子結(jié)點的區(qū)間并正好是父結(jié)點的區(qū)間，可以通過自底向上的計算在每個結(jié)點都計算出當(dāng)前區(qū)間的最大值。
需要注意的是，基于線段樹的二分性質(zhì)，所以它是一棵平衡樹，樹的高度為log(n)。
2、數(shù)據(jù)域
了解線段樹的基本結(jié)構(gòu)以后，看看每個結(jié)點的數(shù)據(jù)域，即需要存儲哪些信息。
首先，既然線段樹的每個結(jié)點表示的是一個區(qū)間，那么必須知道這個結(jié)點管轄的是哪個區(qū)間，所以其中最重要的數(shù)據(jù)域就是區(qū)間左右端點[l, r]。然而有時候為了節(jié)省全局空間，往往不會將區(qū)間端點存儲在結(jié)點中，而是通過遞歸的傳參進行傳遞，實時獲取。
再者，以區(qū)間最大值為例，每個結(jié)點除了需要知道所管轄的區(qū)間范圍[l, r]以外，還需要存儲一個當(dāng)前區(qū)間內(nèi)的最大值max。
圖二-2-1
以數(shù)組A[1:6] = [1 7 2 5 6 3]為例，建立如圖二-2-1的線段樹，葉子結(jié)點的max域為數(shù)組對應(yīng)下標(biāo)的元素值，非葉子結(jié)點的max域則通過自底向上的計算由兩個兒子結(jié)點的max域比較得出。這是一棵初始的線段樹，接下來討論下線段樹的詢問和更新操作。
在詢問某個區(qū)間的最大值時，我們一定可以將這個區(qū)間拆分成log(n)個子區(qū)間，并且這些子區(qū)間一定都能在線段樹的結(jié)點上找到（這一點下文會著重講解），然后只要比較這些結(jié)點的max域，就能得出原區(qū)間的最大值了，因為子區(qū)間數(shù)量為log(n)，所以時間復(fù)雜度是O( log(n) )。
更新數(shù)組某個元素的值時我們首先修改對應(yīng)的葉子結(jié)點的max域，然后修改它的父結(jié)點的max域，以及祖先結(jié)點的max域，換言之，修改的只是線段樹的葉子結(jié)點到根結(jié)點的某一條路徑上的max域，又因為樹高是log(n)，所以這一步操作的時間復(fù)雜度也是log(n)的。
3、指針表示
接下來討論一下結(jié)點的表示法，每個結(jié)點可以看成是一個結(jié)構(gòu)體指針，由數(shù)據(jù)域和指針域組成，其中指針域有兩個，分別為左兒子指針和右兒子指針，分別指向左右子樹；數(shù)據(jù)域存儲對應(yīng)數(shù)據(jù)，根據(jù)情況而定(如果是求區(qū)間最值，就存最值max；求區(qū)間和就存和sum)，這樣就可以利用指針從根結(jié)點進行深度優(yōu)先遍歷了。
以下是簡單的線段樹結(jié)點的C++結(jié)構(gòu)體：
struct treeNode {
Data data; // 數(shù)據(jù)域
treeNode *lson, *rson; // 指針域
}*root;
4、數(shù)組表示
實際計算過程中，還有一種更加方便的表示方法，就是基于數(shù)組的靜態(tài)表示法，需要一個全局的結(jié)構(gòu)體數(shù)組，每個結(jié)點對應(yīng)數(shù)組中的一個元素，利用下標(biāo)索引。
例如，假設(shè)某個結(jié)點在數(shù)組中下標(biāo)為p，那么它的左兒子結(jié)點的下標(biāo)就是2*p，右兒子結(jié)點的下標(biāo)就是2*p+1(類似于一般數(shù)據(jù)結(jié)構(gòu)書上說的堆在數(shù)組中的編號方式)，這樣可以將所有的線段樹結(jié)點存儲在相對連續(xù)的空間內(nèi)。之所以說是相對連續(xù)的空間，是因為有些下標(biāo)可能永遠用不到。
還是以長度為6的數(shù)組為例，如圖二-4-1所示，紅色數(shù)字表示結(jié)點對應(yīng)的數(shù)組下標(biāo)，由于樹的結(jié)構(gòu)和編號方式，導(dǎo)致數(shù)組的第10、11位置空缺。
圖二-4-1
這種存儲方式可以不用存子結(jié)點指針，取而代之的是當(dāng)前結(jié)點的數(shù)組下標(biāo)索引，以下是數(shù)組存儲方式的線段樹結(jié)點的C++結(jié)構(gòu)體：
struct treeNode {
Data data; // 數(shù)據(jù)域
int pid; // 數(shù)組下標(biāo)索引
int lson() { return pid << 1; }
int rson() { return pid<<1|1; } // 利用位運算加速獲取子結(jié)點編號
}nodes[ MAXNODES ];
接下來我們關(guān)心的就是MAXNODES的取值了，由于線段樹是一種二叉樹，所以當(dāng)區(qū)間長度為2的冪時，它正好是一棵滿二叉樹，數(shù)組存儲的利用率達到最高（即100%），根據(jù)等比數(shù)列求和可以得出，滿二叉樹的結(jié)點個數(shù)為2*n-1，其中n為區(qū)間長度（由于C++中數(shù)組長度從0計數(shù)，編號從1開始，所以MAXNODES要取2*n）。那么是否對于所有的區(qū)間長度n都滿足這個公式呢？答案是否定的，當(dāng)區(qū)間長度為6時，最大的結(jié)點編號為13，而公式算出來的是12（2*6）。
那么 MAXNODES 取多少合適呢？
為了保險起見，我們可以先找到比n大的最小的二次冪，然后再套用等比數(shù)列求和公式，這樣就萬無一失了。舉個例子，當(dāng)區(qū)間長度為6時，MAXNODES = 2 * 8；當(dāng)區(qū)間長度為1000，則MAXNODES = 2 * 1024；當(dāng)區(qū)間長度為10000，MAXNODES = 2 * 16384。至于為什么可以這樣，明眼人一看便知。
線段樹的基本操作包括構(gòu)造、更新、詢問，都是深度優(yōu)先搜索的過程。
1、構(gòu)造
線段樹的構(gòu)造是一個二分遞歸的過程，封裝好了之后代碼非常簡潔，總體思路就是從區(qū)間[1, n]開始拆分，拆分方式為二分的形式，將左半?yún)^(qū)間分配給左子樹，右半?yún)^(qū)間分配給右子樹，繼續(xù)遞歸構(gòu)造左右子樹。
當(dāng)區(qū)間拆分到單位區(qū)間時（即遍歷到了線段樹的葉子結(jié)點），則執(zhí)行回溯?；厮輹r對于任何一個非葉子結(jié)點需要根據(jù)兩棵子樹的情況進行統(tǒng)計，計算當(dāng)前結(jié)點的數(shù)據(jù)域，詳見注釋4。
void segtree_build(int p, int l, int r) {
nodes[p].reset(p, l, r); // 注釋1
if (l < r) {
int mid = (l + r) >> 1;
segtree_build(p<<1, l, mid); // 注釋2
segtree_build(p<<1|1, mid+1, r); // 注釋3
nodes[p].updateFromSon(); // 注釋4
}
}
注釋1：初始化第p個結(jié)點的數(shù)據(jù)域，根據(jù)實際情況實現(xiàn)reset函數(shù)
注釋2：遞歸構(gòu)造左子樹
注釋3：遞歸構(gòu)造右子樹
注釋4：回溯，利用左右子樹的信息來更新當(dāng)前結(jié)點，updateFromSon這個函數(shù)的實現(xiàn)需要根據(jù)實際情況進行求解，在第四節(jié)會詳細討論
構(gòu)造線段樹的調(diào)用如下：segtree_build(1, 1, n);
2、更新
線段樹的更新是指更新數(shù)組在[x, y]區(qū)間的值，具體更新這件事情是做了什么要根據(jù)具體情況而定，可以是將[x, y]區(qū)間的值都變成val（覆蓋），也可以是將[x, y]區(qū)間的值都加上val（累加）。
更新過程采用二分，將[1, n]區(qū)間不斷拆分成一個個子區(qū)間[l, r]，當(dāng)更新區(qū)間[x, y]完全覆蓋被拆分的區(qū)間[l, r]時，則更新管轄[l, r]區(qū)間的結(jié)點的數(shù)據(jù)域，詳見注釋2和注釋3。
void segtree_insert(int p, int l, int r, int x, int y, ValueType val) {
if( !is_intersect(l, r, x, y) ) { // 注釋1
return ;
}
if( is_contain(l, r, x, y) ) { // 注釋2
nodes[p].updateByValue(val); // 注釋3
return ;
}
nodes[p].giveLazyToSon(); // 注釋4
int mid = (l + r) >> 1;
segtree_insert(p<<1, l, mid, x, y, val); // 注釋5
segtree_insert(p<<1|1, mid+1, r, x, y, val); // 注釋6
nodes[p].updateFromSon(); // 注釋7
}
注釋1：區(qū)間[l, r]和區(qū)間[x, y]無交集，直接返回
注釋2：區(qū)間[x, y]完全覆蓋[l, r]
注釋3：更新第p個結(jié)點的數(shù)據(jù)域，updateByValue這個函數(shù)的實現(xiàn)需要根據(jù)具體情況而定，會在第四節(jié)進行詳細討論
注釋4：這里先賣個關(guān)子，參見第五節(jié)的lazy-tag
注釋5：遞歸更新左子樹
注釋6：遞歸更新右子樹
注釋7：回溯，利用左右子樹的信息來更新當(dāng)前結(jié)點
更新區(qū)間[x, y]的值為val的調(diào)用如下：segtree_insert(1, 1, n, x, y, val);
3、詢問
線段樹的詢問和更新類似，大部分代碼都是一樣的，只有紅色部分是不同的，同樣是將大區(qū)間[1, n]拆分成一個個小區(qū)間[l, r]，這里需要存儲一個詢問得到的結(jié)果ans，當(dāng)詢問區(qū)間[x, y]完全覆蓋被拆分的區(qū)間[l, r]時，則用管轄[l, r]區(qū)間的結(jié)點的數(shù)據(jù)域來更新ans，詳見注釋1的mergeQuery接口。
void segtree_query (int p, int l, int r, int x, int y, treeNode& ans) {
if( !is_intersect(l, r, x, y) ) {
return ;
}
if( is_contain(l, r, x, y) ) {
ans.mergeQuery(p); // 注釋1
return;
}
nodes[p].giveLazyToSon();
int mid = (l + r) >> 1;
segtree_query(p<<1, l, mid, x, y, ans);
segtree_query(p<<1|1, mid+1, r, x, y, ans);
nodes[p].updateFromSon(); // 注釋2
}
注釋1：更新當(dāng)前解ans，會在第四節(jié)進行詳細討論
注釋2：和更新一樣的代碼，不再累述
四、線段樹的經(jīng)典案例
線段樹的用法千奇百怪，接下來介紹幾個線段樹的經(jīng)典案例，加深對線段樹的理解。
1、區(qū)間最值
區(qū)間最值是最常見的線段樹問題，引例中已經(jīng)提到。接下來從幾個方面來討論下區(qū)間最值是如何運作的。
數(shù)據(jù)域：
int pid; // 數(shù)組索引
int l, r; // 結(jié)點區(qū)間(一般不需要存儲)
ValyeType max; // 區(qū)間最大值
初始化：
void treeNode::reset(int p, int l, int r) {
pid = p;
max = srcArray[l]; // 初始化只對葉子結(jié)點有效
}
單點更新：
void treeNode::updateByValue(ValyeType val) {
max = val;
}
合并結(jié)點：
void treeNode::mergeQuery(int p) {
max = getmax( max, nodes[p].max );
}
回溯統(tǒng)計：
void treeNode::updateFromSon() {
max = nodes[ lson() ].max;
}
結(jié)合上一節(jié)線段樹的基本操作，在構(gòu)造線段樹的時候，對每個結(jié)點執(zhí)行了一次初始化，初始化同時也是單點更新的過程，然后在回溯的時候統(tǒng)計，統(tǒng)計實質(zhì)上是合并左右結(jié)點的過程，合并結(jié)點做的事情就是更新最大值；詢問就是將給定區(qū)間拆成一個個能夠在線段樹結(jié)點上找到的區(qū)間，然后合并這些結(jié)點的過程，合并的結(jié)果ans一般通過引用進行傳參，或者作為全局變量，不過盡量避免使用全局變量。
2、區(qū)間求和
區(qū)間求和問題一般比區(qū)間最值稍稍復(fù)雜一點，因為涉及到區(qū)間更新和區(qū)間詢問，如果更新和詢問都只遍歷到詢問（更新）區(qū)間完全覆蓋結(jié)點區(qū)間的話，會導(dǎo)致計算遺留，舉個例子來說明。
用一個數(shù)據(jù)域sum來記錄線段樹結(jié)點區(qū)間上所有元素的和，初始化所有結(jié)點的sum值都為0，然后在區(qū)間[1, 4]上給每個元素加上4，如圖四-2-1所示：
圖四-2-1
圖中[1, 4]區(qū)間完全覆蓋[1, 3]和[4, 4]兩個子區(qū)間，然后分別將值累加到對應(yīng)結(jié)點的數(shù)據(jù)域sum上，再通過回溯統(tǒng)計sum和，最后得到[1, 6]區(qū)間的sum和為16，看上去貌似天衣無縫，但是實際上操作一多就能看出這樣做是有缺陷的。例如當(dāng)我們要詢問[3, 4]區(qū)間的元素和時，在線段樹結(jié)點上得到被完全覆蓋的兩個子區(qū)間[3, 3]和[4, 4]，累加區(qū)間和為0 + 4 = 4，如圖四-2-2所示。
圖四-2-2
這是因為在進行區(qū)間更新的時候，由于[1, 4]區(qū)間完全覆蓋[1, 3]區(qū)間，所以我們并沒有繼續(xù)往下遍歷，而是直接在[1, 3]這個結(jié)點進行sum值的計算，計算完直接回溯。等到下一次訪問[3, 3]的時候，它并不知道之前在3號位置上其實是有一個累加值4的，但是如果每次更新都更新到葉子結(jié)點，就會使得更新的復(fù)雜度變成O(n)，違背了使用線段樹的初衷，所以這里需要引入一個lazy-tag的概念。
所謂lazy-tag，就是在某個結(jié)點打上一個“懶惰標(biāo)記”，每次更新的時候只要更新區(qū)間完全覆蓋結(jié)點區(qū)間，就在這個結(jié)點打上一個lazy標(biāo)記，這個標(biāo)記的值就是更新的值，表示這個區(qū)間上每個元素都有一個待累加值lazy，然后計算這個結(jié)點的sum，回溯統(tǒng)計sum。
當(dāng)下次訪問到有l(wèi)azy標(biāo)記的結(jié)點時，如果還需要往下訪問它的子結(jié)點，則將它的lazy標(biāo)記傳遞給兩個子結(jié)點，自己的lazy標(biāo)記置空。
這就是為什么在之前在講線段樹的更新和詢問的時候有一個函數(shù)叫g(shù)iveLazyToSon了。接下來看看一些函數(shù)的實現(xiàn)。
數(shù)據(jù)域：
int pid; // 數(shù)組索引
int len; // 結(jié)點區(qū)間長度
ValyeType sum; // 區(qū)間元素和
ValyeType lazy; // lazy tag
初始化：
void treeNode::reset(int p, int l, int r) {
pid = p;
len = r - l + 1;
sum = lazy = 0;
}
單點更新：
void treeNode::updateByValue(ValyeType val) {
lazy += val;
sum += val * len;
}
lazy標(biāo)記繼承：
void treeNode::giveLazyToSon() {
if( lazy ) {
nodes[ lson() ].updateByValue(lazy);
nodes[ rson() ].updateByValue(lazy);
lazy = 0;
}
}
合并結(jié)點：
void treeNode::mergeQuery(int p) {
sum += nodes[p].sum;
}
回溯統(tǒng)計：
void treeNode::updateFromSon() {
sum = nodes[ lson() ].sum;
mergeQuery( rson() );
}
對比區(qū)間最值，區(qū)間求和的幾個函數(shù)的實現(xiàn)主旨是一致的，因為引入了lazy-tag，所以需要多實現(xiàn)一個函數(shù)用于lazy標(biāo)記的繼承，在進行區(qū)間求和的時候還需要記錄一個區(qū)間的長度len，用于更新的時候計算累加的sum值。
3、區(qū)間染色
【例題3】給定一個長度為n(n <= 100000)的木板，支持兩種操作：
1、P a b c 將[a, b]區(qū)間段染色成c；
2、Q a b 詢問[a, b]區(qū)間內(nèi)有多少種顏色；
保證染色的顏色數(shù)少于30種。 對比區(qū)間求和，不同點在于區(qū)間求和的更新是對區(qū)間和進行累加；而這類染色問題則是對區(qū)間的值進行替換（或者叫覆蓋），有一個比較特殊的條件是顏色數(shù)目小于30。
我們是不是要將30種顏色的有無與否都存在線段樹的結(jié)點上呢？答案是肯定的，但是這樣一來每個結(jié)點都要存儲30個bool值，空間太浪費，而且在計算合并操作的時候有一步30個元素的遍歷，大大降低效率。然而30個bool值正好可以壓縮在一個int32中，利用二進制壓縮可以用一個32位的整型完美的存儲30種顏色的有無情況。
因為任何一個整數(shù)都可以分解成二進制整數(shù)，二進制整數(shù)的每一位要么是0，要么是1。二進制整數(shù)的第i位是1表示存在第i種顏色；反之不存在。
數(shù)據(jù)域需要存一個顏色種類的位或和colorBit，一個顏色的lazy標(biāo)記表示這個結(jié)點被完全染成了lazy，基本操作的幾個函數(shù)和區(qū)間求和非常像，這里就不出示代碼了。
和區(qū)間求和不同的是回溯統(tǒng)計的時候，對于兩個子結(jié)點的數(shù)據(jù)域不再是加和，而是位或和。
4、矩形面積并
【例題4】給定n(n <= 100000)個平行于XY軸的矩形，求它們的面積并。如圖四-4-1所示。
圖四-4-1
這類二維的問題同樣也可以用線段樹求解，核心思想是降維，將某一維套用線段樹，另外一維則用來枚舉。具體過程如下：
第一步：將所有矩形拆成兩條垂直于x軸的線段，平行x軸的邊可以舍去，如圖四-4-2所示。圖四-4-2
第二步：定義矩形的兩條垂直于x軸的邊中x坐標(biāo)較小的為入邊，x坐標(biāo)較大的為出邊，入邊權(quán)值為+1，出邊權(quán)值為-1，并將所有的線段按照x坐標(biāo)遞增排序，第i條線段的x坐標(biāo)記為X[i]，如圖四-4-3所示。
圖四-4-3
第三步：將所有矩形端點的y坐標(biāo)進行重映射(也可以叫離散化)，原因是坐標(biāo)有可能很大而且不一定是整數(shù)，將原坐標(biāo)映射成小范圍的整數(shù)可以作為數(shù)組下標(biāo)，更方便計算，映射可以將所有y坐標(biāo)進行排序去重，然后二分查找確定映射后的值，離散化的具體步驟下文會詳細講解。如圖四-4-4所示，藍色數(shù)字表示的是離散后的坐標(biāo)，即1、2、3、4分別對應(yīng)原先的5、10、23、25（需支持正查和反查）。假設(shè)離散后的y方向的坐標(biāo)個數(shù)為m，則y方向被分割成m-1個獨立單元，下文稱這些獨立單元為“單位線段”，分別記為<1-2>、<2-3>、<3-4>。
圖四-4-4
第四步：以x坐標(biāo)遞增的方式枚舉每條垂直線段，y方向用一個長度為m-1的數(shù)組來維護“單位線段”的權(quán)值，如圖四-4-5所示，展示了每條線段按x遞增方式插入之后每個“單位線段”的權(quán)值。
當(dāng)枚舉到第i條線段時，檢查所有“單位線段”的權(quán)值，所有權(quán)值大于零的“單位線段”的實際長度之和(離散化前的長度)被稱為“合法長度”，記為L，那么(X[i] - X[i-1]) * L，就是第i條線段和第i-1條線段之間的矩形面積和，計算完第i條垂直線段后將它插入，所謂"插入"就是利用該線段的權(quán)值更新該線段對應(yīng)的“單位線段”的權(quán)值和（這里的更新就是累加）。
圖四-4-5
如圖四-4-6所示：紅色、黃色、藍色三個矩形分別是3對相鄰線段間的矩形面積和，其中紅色部分的y方向由<1-2>、<2-3>兩個“單位線段”組成，黃色部分的y方向由<1-2>、<2-3>、<3-4>三個“單位線段”組成，藍色部分的y方向由<2-3>、<3-4>兩個“單位線段”組成。特殊的，在計算藍色部分的時候，<1-2>部分的權(quán)值由于第3條線段的插入(第3條線段權(quán)值為-1)而變?yōu)榱?，所以不能計?#8220;合法長度”。
以上所有相鄰線段之間的面積和就是最后要求的矩形面積并。
圖四-4-6
那么這里帶來幾個問題：
1、是否任意相鄰兩條垂直x軸的線段之間組成的封閉圖形都是矩形呢？答案是否定的，如圖四-4-7所示，其中綠色部分為四個矩形的面積并中的某塊有效部分，它們同處于兩條相鄰線段之間，但是中間有空隙，所以它并不是一個完整的矩形。
2、每次枚舉一條垂直線段的時候，需要檢查所有“單位線段”的權(quán)值，如果用數(shù)組維護權(quán)值，那么這一步檢查操作是O(m)的，所以總的時間復(fù)雜度為O(nm)，其中n表示垂直線段的個數(shù)，復(fù)雜度太大需要優(yōu)化。
圖四-4-7
優(yōu)化自然就是用線段樹了，之前提到了降維的思想，x方向我們繼續(xù)采用枚舉，而y方向的“單位線段”則可以采用線段樹來維護，和一般問題一樣，首先討論數(shù)據(jù)域。
數(shù)據(jù)域：
int pid; // 數(shù)組索引
int l, r; // 結(jié)點代表的“單位線段”區(qū)間[l, r] (注意，l和r均為離散后的下標(biāo))
int cover; // [l, r]區(qū)間被完全覆蓋的次數(shù)
int len; // 該結(jié)點表示的區(qū)間內(nèi)的合法長度
注意，這次的線段樹和之前的線段樹稍微有點區(qū)別，就是葉子結(jié)點的區(qū)間端點不再相等，而是相差1，即l+1 == r。因為一個點對于計算面積來說是沒有意義的。
算法采用深度優(yōu)先搜索的后序遍歷，記插入線段為[a, b, v]，其中[a, b]為線段的兩個端點，是離散化后的坐標(biāo)；v是+1或-1，代表是入邊還是出邊，每次插入操作二分枚舉區(qū)間，當(dāng)線段樹的結(jié)點代表的區(qū)間被插入?yún)^(qū)間完全覆蓋時，將權(quán)值v累加到結(jié)點的cover域上。由于是后續(xù)遍歷，在子樹全部遍歷完畢后需要進行統(tǒng)計。插入過程修改cover，同時更新len。
回溯統(tǒng)計過程對cover域分情況討論：
當(dāng)cover > 0時，表示該結(jié)點代表的區(qū)間至少有一條入邊沒有被出邊抵消，換言之，這塊區(qū)間都應(yīng)該在“合法長度”之內(nèi)，則 len = Y[r] - Y[l]（Y[i]代表離散前第i大的點的y坐標(biāo)）；更加通俗的理解是至少存在一個矩形的入邊被掃描到了，而出邊還未被掃描到，所以這塊面積需要被計算進來。
當(dāng)cover等于0時，如果該區(qū)間是一個單位區(qū)間（即上文所說的“單位線段”，l+1 == r，也是線段樹的葉子結(jié)點），則 len = 0；否則，len需要由左子樹和右子樹的計算結(jié)果得出，又因為是后序遍歷，所以左右子樹的len都已經(jīng)計算完畢，從而不需要再進行遞歸求解，直接將左右兒子的len加和就是答案，即len = lson.len + rson.len。
圖四-4-8
圖四-4-8所示為上述例子的初始線段樹，其中根結(jié)點管轄的區(qū)間為[1, 4]，代表"單位線段”的兩個端點。對于線段樹上任何一棵子樹而言，根結(jié)點管轄區(qū)間為[l, r]，并且mid = (l + r) / 2，那么如果它不是葉子結(jié)點，則它的左子樹管轄的區(qū)間就是[l, mid]，右子樹管轄的區(qū)間就是[mid, r]。葉子結(jié)點管轄區(qū)間的左右端點之差為1（和之前的線段樹的區(qū)間分配方式稍有不同）。
這樣就可以利用二分，在O(n)的時間內(nèi)遞歸構(gòu)造初始的線段樹。
圖四-4-9
圖四-4-9所示為插入第一條垂直線段[1, 3, 1]（插入?yún)^(qū)間[1, 3]，權(quán)值為1）后的情況，插入過程類似建樹過程，二分遞歸執(zhí)行插入操作，當(dāng)插入?yún)^(qū)間完全覆蓋線段樹結(jié)點區(qū)間時，將權(quán)值累加到對應(yīng)結(jié)點（圖中綠色箭頭指向的結(jié)點）的cover域上；否則，繼續(xù)遞歸左右子樹。然后進行自底向上的統(tǒng)計，統(tǒng)計的是len的值。
[2, 4]這個結(jié)點的cover域為0，所以它的len等于兩棵子樹的len之和，[1, 4]亦然。
圖四-4-10
圖四-4-10所示為插入第二條垂直線段[2, 4, 1]（插入?yún)^(qū)間[2, 4]，權(quán)值為1）后的情況，只需要修改一個結(jié)點（圖中綠色箭頭指向的結(jié)點）的cover域，該結(jié)點的兩棵子樹不需要再進行遞歸計算，回溯的時候，計算根結(jié)點len值時，由于根結(jié)點的cover域為0，所以它的len等于左右子樹的len之和。
圖四-4-11
圖四-4-11所示為插入第三條垂直線段[1, 3, -1]（插入?yún)^(qū)間[1, 3]，權(quán)值為-1）后的情況，直觀的看，現(xiàn)在Y方向只有[2, 4]一條線段了，所以根結(jié)點的len就是Y[4] - Y[2] = 15。
講完插入，就要談?wù)勗儐?。在每次插入之前，需要詢問之前插入的線段中，在y方向的“合法長度”L，根據(jù)線段樹結(jié)點的定義，y方向“合法長度”總和其實就是根結(jié)點的len，所以這一步詢問操作其實是O(1)的，在插入過程中已經(jīng)實時計算出來，再加上插入的O(log n)的時間復(fù)雜度，已經(jīng)完美解決了上述復(fù)雜度太大的問題了。
5、區(qū)間K大數(shù)
【例題5】給定n(n <= 100000)個數(shù)的數(shù)組，然后m(m <= 100000)條詢問，詢問格式如下：
1、l r k 詢問[l, r]的第K大的數(sh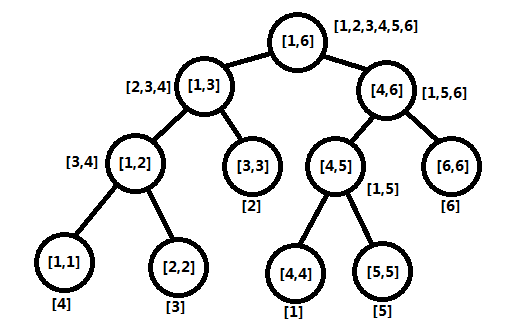ù)的值 
圖四-5-1
從圖中可以看出，線段樹的任何一個結(jié)點存儲了對應(yīng)區(qū)間的數(shù)，并且進行有序排列，所以根結(jié)點存儲的一定是一個長度為數(shù)組總長的有序數(shù)組，葉子結(jié)點存儲的遞增序列為原數(shù)組元素。
每次詢問，我們將給定區(qū)間拆分成一個個線段樹上的子區(qū)間，然后二分枚舉答案T，再利用二分查找統(tǒng)計這些子區(qū)間中大于等于T的數(shù)的個數(shù)，從而確定T是否是第K大的。
對于區(qū)間K大數(shù)的問題，還有很多數(shù)據(jù)結(jié)構(gòu)都能解決，這里僅作簡單介紹。
五、線段樹的常用技巧
1、離散化
在講解矩形面積并的時候曾經(jīng)提了一下離散化，現(xiàn)在再詳細的說明一下，所謂離散化就是將無限的個體映射到有限的個體中，從而提高算法效率。
舉個簡單的例子，一個實數(shù)數(shù)組，我想很快的得到某個數(shù)在整個數(shù)組里是第幾大的，并且詢問數(shù)很多，不允許每次都遍歷數(shù)組進行比較。
那么，最直觀的想法就是對原數(shù)組先進行一個排序，詢問的時候只需要通過二分查找就能在O( log(n) )的時間內(nèi)得出這個數(shù)是第幾大的了，離散化就是做了這一步映射。
對于一個數(shù)組[1.6, 7.8, 5.5, 11.1111, 99999, 5.5]，離散化就是將原來的實數(shù)映射成整數(shù)(下標(biāo))，如圖五-1-1所示：
圖五-1-1
這樣就可以將原來的實數(shù)保存在一個有序數(shù)組中，詢問第K大的是什么稱為正查，可以利用下標(biāo)索引在O(1)的時間內(nèi)得到答案；詢問某個數(shù)是第幾大的稱為反查，可以利用二分查找或者Hash得到答案，復(fù)雜度取決于具體算法，一般為O(log(n))。
2、lazy-tag
這個標(biāo)記一般用于處理線段樹的區(qū)間更新。
線段樹在進行區(qū)間更新的時候，為了提高更新的效率，所以每次更新只更新到更新區(qū)間完全覆蓋線段樹結(jié)點區(qū)間為止，這樣就會導(dǎo)致被更新結(jié)點的子孫結(jié)點的區(qū)間得不到需要更新的信息，所以在被更新結(jié)點上打上一個標(biāo)記，稱為lazy-tag，等到下次訪問這個結(jié)點的子結(jié)點時再將這個標(biāo)記傳遞給子結(jié)點，所以也可以叫延遲標(biāo)記。
3、子樹收縮
子樹收縮是子樹繼承的逆過程，子樹繼承是為了兩棵子樹獲得父結(jié)點的信息；而子樹收縮則是在回溯的時候，如果兩棵子樹擁有相同數(shù)據(jù)的時候在將數(shù)據(jù)傳遞給父結(jié)點，子樹的數(shù)據(jù)清空，這樣下次在訪問的時候就可以減少訪問的結(jié)點數(shù)。
六、線段樹的多維推廣
1、二維線段樹 - 矩形樹
線段樹是處理區(qū)間問題的，二維線段樹就是處理平面問題的了，曾經(jīng)寫過一篇二維線段樹的文章，就不貼過來了，直接給出傳送門：二維線段樹。 2、三維線段樹 - 空間樹
線段樹-二叉樹，二維線段樹-四叉樹，三維線段樹自然就是八叉樹了，分割的是空間，一般用于三維計算幾何，當(dāng)然也不一定用在實質(zhì)的空間內(nèi)的問題。
比如需要找出身高、體重、年齡在一定范圍內(nèi)并且顏值最高的女子，就可以用三維線段樹（三維空間最值問題），嘿嘿嘿?。。?/strong>
七、線段樹相關(guān)題集整理
Coder ★★★☆☆ 求和-線段樹 + 樹狀數(shù)組 區(qū)間染色
LCIS ★★★☆☆ 染色-最長連續(xù)遞增子序列 Man Down ★★★☆☆ 動態(tài)規(guī)劃 + 區(qū)間染色 矩形問題二維線段樹