AC自動機
算法目的：
AC自動機主要用于解決多模式串的匹配問題，是字典樹(trie樹)的變種，一種偽樹形結構(主體是樹形的，但是由于加入了失敗指針，使得它變成了一個有向圖)；trie圖(我的理解^_^)是對AC自動機的一種改造，使得圖中每個結點都有MAXC條出邊(MAXC表示該圖的字符集合大小), trie圖上的每個結點代表一個狀態，并且和AC自動機的結點是一一對應的。
算法核心思想：
學習AC自動機(AC-Automan？艾斯奧特曼？-_-|||)之前，首先需要有字典樹和KMP的基礎，這是每一篇關于AC自動機的文章都會論及的，所以我也就例行提一下。
例如，有四個01字符串(模式串)，"01"、"10"、"110"、"11"，字符集合為{'0', '1'}。那么構造trie圖分三步，首先建立字典樹，然后構造失敗指針，最后通過失敗指針補上原來不存在的邊，那么現在就分三步來討論如何構建一個完整的trie圖。
圖1
1) 字典樹
字典樹是一種樹形結構，它將所有的模式串組織在一棵樹的樹邊上，它的根結點是一個虛根，每條樹邊代表一個字母，從根結點到任意一個結點的路徑上的邊的有序集合代表某個模式串的某個前綴。
如圖1，綠色點為虛根，藍色點為內部結點，紅色點為終止結點，即從根結點到終止結點的每條路徑代表了一個模式串，由于"11"是"110"的前綴，所以在圖中"11"這兩條邊是這兩個字符串路徑的共用部分，這樣就節省了存儲空間，由于trie樹的根結點到每個結點的路徑(邊權)都代表了一個模式串的前綴，所以它又叫前綴樹。
字典樹實際上是一個DFA(確定性有限狀態自動機)，通常用轉移矩陣表示。行表示狀態，列表示輸入字符，(行, 列)位置表示轉移狀態。這種方式的查詢效率很高，但由于稀疏的現象嚴重，空間利用效率很低。所以一般采用壓縮的存儲方式即鏈表來表示狀態轉移，每個結點存儲至少兩個域：數據域data、子結點指針域next[MAXC](其中MAXC表示字符集總數)。
構造字典樹的前提一般是給定一系列的模式串，然后對每個模式串進行插入字典樹的操作，初始情況下字典樹只有一個虛根，如圖2所示，進行四個模式串的插入后就完成了圖1中的字典樹的構造，每次插入在末尾結點打上標記(圖中紅色部分)，可以注意到，第四次操作實際上沒有生成新的結點，只是打了一個結尾標記，由于它的這個性質，使得字典樹的結點數目不會很多，大大壓縮了存儲結構。具體實現方式和編碼會在下文中詳細講解。
圖2
2)
失敗指針
給定一個目標串，要求在由模式串構建的字典樹中查找這個目標串中有多少個模式串，我們可以設定一個指針p，初始狀態下它指向根結點，然后從前往后枚舉目標串，對每一個目標串中的字符c，如果在p指向結點的出邊集合中能夠找到字符c對應的邊，那么將p指向c對應邊的子結點，循環往復，直到匹配失敗，那么退回到p結點的fail指針指向的結點繼續同樣的匹配，當遇到一個終止結點時，計數器+1。
這里的fail指針類似KMP的next函數，每個trie結點都有一個fail指針，如圖3，首先將根結點的fail指針指向NULL，根結點的直接子結點的fail指針指向根結點，這一步是很顯然的，因為當一個字符都不能匹配的時候肯定是要跳到字符串首重新匹配了，每個結點的fail指針都是由它父結點的fail指針決定的，所以一次BFS就可以把所有結點的fail指針逐層求解出來了，具體實現方式和編碼會在下文中詳細講解。
圖3
3)
trie圖
為了方便描述，我們先把所有trie樹上的結點進行編號，編號順序為結點的插入順序，根結點編號為0。如圖4的第一個圖，我們發現如果現在是1號狀態(狀態即結點)，當接收一個'1'這個字符，那么它應該進入哪個狀態呢？答案很顯然，是2號狀態，因為沿著字符'1'的出邊到達的狀態正好是2號狀態；但是如果接受的是'0'字符，我們發現1號狀態沒有'0'字符代表的出邊，所以我們需要補上這條'0'邊，但是這條邊指向哪個狀態呢？答案是1號狀態的fail指針指向的狀態的'0'出邊對應的狀態。我們發現這個狀態正好是它自己，所以向自己補一條邊權為'0'的邊(圖中的橙色邊，邊指向的結點稱為當前狀態的后繼狀態)。同樣是利用BFS的方式逐層求解所有結點的后繼狀態。我們發現所有結點遍歷完后，每個結點都有且僅有兩條出邊，這樣一個trie圖就誕生了。
圖4
今后幾乎所有關于狀態機的問題都是圍繞圖4的那個圖展開的。
新手初看算法的時候總是一頭霧水，即使看懂了也要花很大力氣才能把代碼寫出來(至少我是這樣的)，所以沒有什么比直接闡述代碼更加直觀的了。
一、結構定義
1 #define MAXC 26
2 // 結點結構
3 struct ACNode {
4 public:
5 ACNode *fail; // fail指針，指向和當前結點的某個后綴匹配的最長前綴的位置
6 ACNode *next[MAXC]; // 子結點指針
7
8 // 以下這些數據需要針對不同題目，進行適當的注釋，因為可能內存會吃不消
9
10 int id; // 結點編號(每個結點有一個唯一編號)
11 int val; // 當前結點和它的fail指針指向結點的結尾單詞信息的集合
12 int cnt; // 有些題中模式串有可能會有多個單詞是相同的，但是計數的時候算多個
13
14 void reset(int _id) {
15 id = _id;
16 val = 0;
17 cnt = 0;
18 fail = NULL;
19 memset(next, 0, sizeof(next));
20 }
21
22 // 狀態機中的 接收態 的概念
23 // 模式串為不能出現(即病毒串)的時候才有接收態
24 bool isReceiving() {
25 return val != 0;
26 }
27 };
對于trie樹上的每個結點，保存了以下數據域：
1) 結點編號 int id;
每個結點的唯一標識，用于狀態轉移的時候的下標映射。
2) 子結點指針 ACNode *next[MAXC];
每個結點的子結點的個數就是字符串中字符集的大小，一般為26個英文字母，當然也有特殊情況，比如說和DNA有關的題，字符集為{ 'A'、'C'、'G'、'T'
}，那么字符集大小就為4；和二進制串有關的題，字符集大小就為2；而有的題則包含了所有的可見字符，所以字符集大小為256(有可能有中文字符...太BT了)，這個就要視情況而定了。
3) 失敗指針 ACNode *fail;
它的含義類似KMP中的最長前后綴的概念，即目標串在trie樹上進行匹配的時候，如果在P結點上匹配失敗，那么應該跳到P->fail繼續匹配，如果還是失敗，那么跳到P->fail->fail繼續匹配，對于這個fail指針的構造，下文會詳細講解，這里先行跳過。
4) 結尾標記 int cnt, val;
每個模式串在進行插入的過程中，會對模式串本身進行一次線性的遍歷，當遍歷完畢即表示將整個串插入完畢，在結尾結點需要一個標記，表示它是一個模式串的末尾，有些問題會出現多個相同的模式串，所以用cnt來表示該串出現的次數，每插入一次對cnt進行一次自增；而有的題中，相同的模式串有不同的權值，并且模式串的個數較少(<= 15)，那么可以將該結點是否是模式串的末尾用2的冪來表示，壓縮成二進制的整數記錄在val上(例如當前結點是第二個模式串和第四個模式串的結尾，則val = (1010)2)。
1 class ACAutoman {
2 public:
3 /*結點相關結構*/
4 ACNode* nodes[MAXQ]; // 結點緩存，避免內存重復申請和釋放，節省時間
5 int nodesMax; // 緩沖區大小，永遠是遞增的
6 ACNode *root; // 根結點指針
7 int nodeCount; // 結點總數
8
9 /*數據相關結構*/
10 int ID[256], IDSize; // 結點上字母的簡單HASH，使得結點編號在數組中連續
11 // 例如： ID['a']=0 ID['b']=1 依此類推
12
13 /*隊列相關結構*/
14 ACNodeQueue Q;
15
16 public:
17 ACAutoman() {
18 nodesMax = 0;
19 }
20 // 初始化！??！ 必須調用
21 void init() {
22 nodeCount = 0;
23 IDSize = 0;
24 root = getNode();
25 memset(ID, -1, sizeof(ID));
26 }
27
28 // 獲取結點
29 ACNode *getNode() {
30 // 內存池已滿，需要申請新的結點
31 if(nodeCount >= nodesMax) {
32 nodes[nodesMax++] = new ACNode();
33 }
34 ACNode *p = nodes[nodeCount];
35 p->reset(nodeCount++);
36 return p;
37 }
38
39 // 獲取字母對應的ID
40 int getCharID(unsigned char c, int needcreate) {
41 if(!needcreate) return ID[c];
42 if(ID[c] == -1) ID[c] = IDSize++;
43 return ID[c];
44 }
45 }AC;
終于看到故事的主角(ACAutoman, 艾斯奧特曼)了，同樣介紹一下它需要維護的數據結構：
1) 結點緩存 ACNode* nodes[MAXQ];
為了方便訪問，我們將所有的結點組織在一個數組中，并且一開始不開辟空間，每次需要一個結點的時候，利用接口getNode()獲取，類似內存池的概念，避免頻繁申請和釋放內存時候的時間開銷。
2) 根結點指針ACNode *root;
trie樹，既然是樹，自然是有一個根結點的嘛。
3) 結點總數 int nodeCount;
4) 結點隊列 ACNodeQueue Q;
ACNodeQueue是自己實現的一個隊列，數據域為ACNode *，主要是因為STL的效率實在不敢恭維，在某些OJ上效率極低，自己封裝一套比較好，這個隊列會在BFS的時候求失敗指針時用到。
二、模式串插入
1 void ACAutoman ::insert(char *str, int val) {
2 ACNode *p = root;
3 int id;
4 for(int i = 0; str[i]; i++) {
5 // 獲取字母對應的哈希ID
6 id = getCharID(str[i], true);
7 // 檢查子結點是否存在，不存在則創建新的子結點
8 if(p->next[id] == NULL) p->next[id] = getNode();
9 p = p->next[id];
10 }
11 // 在這個單詞的結尾打上一個標記
12 p->val |= val; // 注意有可能有相同的串
13 p->cnt ++;
14 }
str為模式串，將它插入到trie樹時，需要進行一次線性遍歷，為了使每個字符訪問方便，我們將字母映射到整數區間[0, IDSize)中，只要采用最簡單的哈希即可。初始化當前結點p為根結點，對于字符串的某個字符，轉換成整數id后，檢測當前結點p是否存在id這個子結點，如果不存在則利用getNode()獲取一個新的結點，并且讓當前結點p的id子結點指向它，然后將當前結點轉到它的id子結點上，繼續上述操作。直到整個模式串枚舉完畢，在結點p打上結束標記即可。
三、失敗指針、trie圖
構造
1 void construct_trie() {
2 ACNode *now, *son, *tmp;
3
4 root->fail = NULL;
5 Q.clear();
6 Q.push(root);
7
8 // 逐層計算每一層的結點的fail指針
9 // 當每個結點計算完畢，保證它所有后繼都已經計算出來
10 while( !Q.empty() ) {
11 now = Q.pop();
12
13 if(now->fail) {
14 // 這里需要視情況而定
15 // 目的是將fail指針的狀態信息傳遞給當前結點
16 // now->val += now->fail->val;
17 // now->val |= now->fail->val;
18
19 // 如果當前結點是個接收態，那么它的所有后繼都是回到本身
20 if(now->isReceiving()) {
21 for(int i = 0; i < MAXC; i++) {
22 now->next[i] = now;
23 }
24 continue;
25 }
26 }
27 // 首先，我們把當前結點now的i號后繼記為son[i]
28 // i) 如果son[i]不存在，將它指向 當前結點now的fail指針指向結點的i號后繼(保證一定已經計算出來)。
29 // 2) 如果son[i]存在，將它的fail指針指向 當前結點now的fail指針指向結點的i號后繼(保證一定已經計算出來)。
30 for(int i = 0; i < MAXC; i++) {
31 son = now->next[i];
32 tmp = (now == root) ? root : now->fail->next[i];
33 if(son == NULL) {
34 now->next[i] = tmp;
35 }else {
36 son->fail = tmp;
37 Q.push(son);
38 }
39 }
40 }
41 }
首先，講一下失敗指針的含義，因為之前提到，一個模式串的某個字符匹配失敗的時候，就跳到它的失敗指針上繼續匹配，重復上述操作，直到這個字符匹配成功，所以失敗指針一定滿足一個性質，它指向的一定是某個串的前綴，并且這個前綴是當前結點所在前綴的后綴，而且一定是最長后綴。仔細理解一下這句話，首先，一定是某個串的前綴，這是顯然的，因為trie樹本來就是前綴樹，它的任意一個結點都是某個模式串的前綴；然后再來看后面一句話，為了讓當前字符能夠找到匹配，那么當前結點的某個后綴必須要和某個模式串的前綴相匹配，這個性質就和KMP的next數組不謀而合了。
然后，就是來看如何利用BFS求出所有結點的失敗指針了。
1) 對于根結點root的失敗指針，我們將它直接指向NULL，對于根結點下所有的子結點，失敗指針一定是指向root的，因為當一個字符都不能匹配的時候，自然也就不存在更短的能夠與之匹配的前綴了；
2) 將求完失敗指針的結點插入隊列中；
3) 每次彈出一個結點now，詢問它的每個字符對應的子結點，為了闡述方便，我們將now的i號子結點記為now->next[i]：
a) 如果now->next[i]為NULL，那么將now->next[i]指向now的失敗指針的i號子結點,
即
now->next[i] = now->fail->next[i];
b) 如果now->next[i]不等于NULL，則需要構造now->next[i]的失敗指針，由于a)的操作，我們知道now的失敗指針一定存在一個i號子結點，即now->fail->next[i]，那么我們將now->next[i]的失敗指針指向它，即now->next[i]->fail
= now->fail->next[i]；
4) 重復2)的操作直到隊列為空；
四、目標串匹配
1 int query_str(char *str) {
2 ACNode *p = root, *tmp = NULL;
3 int id;
4 int cnt = 0;
5
6 for(int i = 0; str[i]; i++) {
7 id = getCharID(str[i], false);
8 if(id == -1) {
9 // 當前單詞從來沒有出現過，直接回到匹配之初
10 p = root;
11 continue;
12 }
13 p = p->next[id];
14 tmp = p;
15 while(tmp != root && tmp->cnt != -1) {
16 if(tmp->cnt) {
17 // 找到一個子串以tmp結點結尾
18 // 這里一般需要做題目要求的操作，不同題目不同
19 // 有的是統計子串數目、有的則是輸出子串位置
20 cnt += tmp->cnt;
21 tmp->cnt = -1;
22 }
23 tmp = tmp->fail;
24 }
25 }
26 return cnt;
27 }
對目標串進行匹配的時候，同樣需要掃描目標字符串。由于trie圖已經創建完畢，每個結點讀入一個字符的時候都能夠進入到下一個狀態，所以我們只需要根據目標串給定的字符進行遍歷，然后每次檢查當前的結點是否是結尾結點，當然還需要檢查p的失敗指針指向的結點...累加所有的cnt和即為模式串的個數。
對于AC自動機，各大OJ都有相關習題，來看幾道比較經典的：
HDU 2222 Keywords
Search
題意：給定N(N <= 10000)個長度不大于50的模式串，再給定一個長度為L(L
<= 106)目標串，求目標串出現了多少個模式串。
題解：AC自動機模板題，在每個trie結點存儲一個count值，每次插入一個單詞的時候對單詞結尾結點的count值進行自增(不能將count值直接置為1，因為有可能模式串中有多個相同的串，它們是要被算作多次的)，然后在詢問的時候，每次計數完畢之后，將count值標為-1表示它已經被計算過了。最后輸出所有count的累加和即可。
HDU 2896 病毒侵襲
題意：N(N <= 500)個長度不大于200的模式串(保證所有的模式串都不相同)，M(M <= 1000)個長度不大于10000的待匹配串，問待匹配串中有哪幾個模式串，題目保證每個待匹配串中最多有三個模式串。
題解：構造trie樹和fail指針，由于每個模式串都不同，所以每個代表模式串結尾的trie結點存儲模式串對應的編號idx，掃描所有帶匹配串，對于每個待匹配串利用失敗指針模擬匹配，匹配的模式串個數到達三個的時候放棄掃描該串。
可見字符包括空格，所以讀入的時候需要用gets()，子結點個數為128。
HDU 3065 病毒侵襲持續中
題意：N(N <= 1000)個長度不大于50的模式串(保證所有的模式串都不相同)，一個長度不大于2000000的待匹配串，求模式串在待匹配串中的出現次數。
題解：由于每個病毒串不會完全相同，對于每個病毒串末尾記錄一個編號標記，完全匹配后對編號對應的數組進行累加和計算。
PKU 1204 Word Puzzles
題意：給定一個L x C(C <= 1000, L <= 1000)的字母矩陣，再給定W(W <= 1000)個字符串，保證這些字符串都會在字母矩陣中出現(8種方向)，求它們的出現位置和方向。
題解：先緩存所有數據，然后對W個字符串建立字典樹和失敗指針，再掃描字母矩陣所有8個方向的字符串進行匹配。
ZJY 3228 Searching the String
題意：給定一個長度為N(N <= 105)的目標串，然后再給定M(M <= 105)個長度不大于6的字符串，問這些字符串在目標串的出現次數(分可重疊和不可重疊兩種)。
題解：將M個串作為模式串建立自動機，對于可重疊的情況直接詢問即可，類似HDU 3065，不可重疊的情況需要記錄每個串的長度Li以及之前這個串匹配到的最大位置Pi，對于當前位置Pos，如果Pi +
Li <= Pos，那么認為和之前的一次匹配沒有重疊，計數累加，并且更新Pi = Pos。
為了方便，我把兩種計算方式的模式串分別建立了兩個自動機。
PKU 3208 Apocalypse Someday
題意：求第K(K <= 5*107)個有連續3個6的數。
題解：建立DFA如下圖，其中0為初態，1為非法狀態(存在前導0)，2為后綴沒有6的狀態，3、4、5分別為后綴有1個、2個、3個6的狀態，所以5為接收態，因為一旦出現了3個6，那么無論接下來的是什么數都認為是合法數。
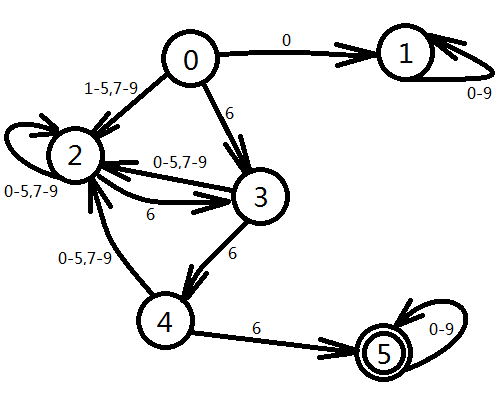
既然有了狀態轉移圖就可以輕松地利用狀態轉移方程求出長度為n有連續3個6的數字的個數，當長度小于等于L的滿足條件的數字總數大于等于K的時候，就表明第K個滿足條件的數字的長度為L，然后枚舉每一位的數字判可行即可。
PKU 2778 DNA Sequence
題意：給定m(m <= 10)個DNA片段，每個串長度不超過10。求長度為N(N <= 2*109)的串中不包括任何給定的DNA片段的串的總數。
題解：利用模式串建立trie圖，將trie圖轉化為矩陣表示，利用二分求冪加速。
為了更加直觀，舉例說明：
例如，m=2，兩個DNA片段分別為A和CAG，可以建立如下AC自動機：
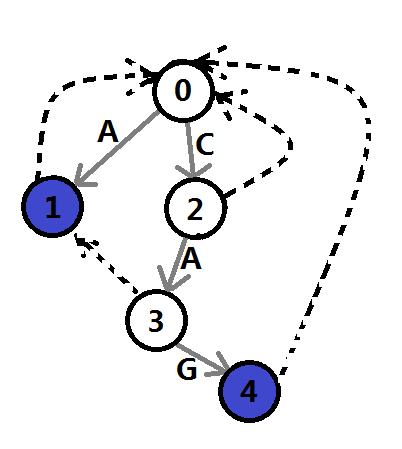
圖5
其中，灰色箭頭代表樹邊，虛線代表失敗指針，藍色結點代表終止狀態，0為起始狀態。
然后我們利用它來構造trie圖，如圖6。
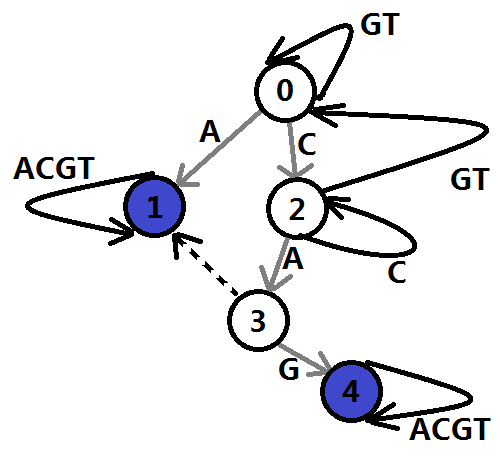
圖6
構造方法是利用BFS，依次處理每個狀態可以到達哪些狀態，建立可達矩陣。
具體步驟如下：
1) 初始狀態入隊。
2) 每次彈出一個狀態結點進行處理，直到隊列為空。
a) 對于當前處理的結點P，判斷P是否是一個終止結點，如果不是，則判斷P的fail指針指向的是否是一個終止結點，一直迭代到fail指針為空，如果迭代過程中找到某個結點為終止結點，那么表示P所在串的某個后綴包含了給定的DNA片段，那么標記P為終止結點，重復2)，否則轉b)。
b) 枚舉P的所有子結點Q[i](這里的子結點是包含所有字符集的)：
i) 如果Q[i]這個結點不為空，那么DFA[P][Q[i]] ++，Q[i]入隊；
ii) 否則沿著P的fail指針一直找，直到找到一個結點S的對應子結點T[i]不為空，那么DFA[P][T[i]]++，如果一直找不到，那么DFA[P][root]++;
當隊列為空的時候，有限狀態自動機也就構造完畢了，按照這種方式，我們可以發現，除了終止狀態，所有狀態都有四條出邊(A、C、G、T)，但是終止狀態并非真正意義上的終止狀態，于是我們在終止狀態上添加四條回邊(指向自己)，表示如果狀態進入了終止狀態就再也出不去了，這樣一來，這個狀態機就完整了，任意一個狀態只要接收A、C、G、T四個字符中的一個就能進入下一個狀態，這樣就轉化成了一個動態規劃問題，假設狀態方程DP[i][j]表示長度為i的串在j狀態下的字符串個數，那么對于圖2的狀態機，有如下關系：
DP[i][0] = 2 *
DP[i-1][2] + 2 * DP[i-1][0];
DP[i][1] =
DP[i-1][0] + 4 * DP[i-1][1];
DP[i][2] =
DP[i-1][0] + DP[i-1][2];
DP[i][3] =
DP[i-1][2] + 4*DP[i-1][3];
由于在DFA狀態處理的時候3號狀態為終止狀態，所以DP[i][4]其實已經是一個冗余狀態了，所以不列入討論范圍。
按照遞推方程，DP[N][0] + DP[N][2]就是我們要求的答案，但是N很大，所以可以將DP轉移轉化成矩陣，即：
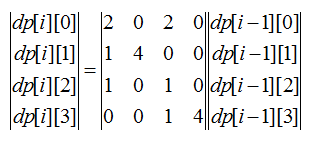
然后利用矩陣的二分求冪來加速了。
這題更加直觀的理解是：從起點0開始，走N步，經過的路徑就是一個DNA串，如果最后到達的是終止狀態，那么表示它包含了m個DNA片段中的至少一個。所有路徑長度為N，終點非終止狀態的路徑數目之和就是我們要求的解。
PKU 1625 Censored!
題意：給定p(p <= 10)個長度不大于10的模式串，求長度為m(m <= 50)的串中不包含任何模式串的串的種類數。
題解：首先利用模式串建立trie圖，用DP[i][j]表示長度為i，狀態為j的字符串的種類數，枚舉所有字符進行狀態轉移即可。最后Sum{DP[m][i], i表示非終止狀態} 就是答案，這題如果將字符直接進行下標映射，有可能會RE，就是它的字符的ASCII碼有可能是在128-255之間的(例如中文)，如果用scanf讀入，轉換成char就變成了負數，如果映射到下標就RE了，所以在映射之前最好先轉成unsigned char。
PKU 3691 DNA repair
題意：給定N(N <= 50)個長度不超過20的模式串，再給定一個長度為M(M <= 1000)的目標串S，求在目標串S上最少改變多少字符，可以使得它不包含任何的模式串（所有串只有ACGT四種字符）。
題解：利用模式串建立trie圖，trie圖的每個結點(即下文講到的狀態j)維護三個結構，
Node{
Node *next[4]; // 能夠到達的四個狀態 的結點指針
int
id; // 狀態ID，用于到數組下標的映射
int
val; // 當前狀態是否是一個非法狀態 （以某些模式串結尾）
}
用DP[i][j]表示長度為i (i <= 1000)，狀態為j(j <= 50*20 + 1)的字符串變成目標串S需要改變的最少字符，設初始狀態j = 0，那么DP[0][0] = 0，其它的DP[i][j]均為無窮大。從長度i到i+1進行狀態轉移，每次轉移枚舉共四個字符(A、C、G、T)，如果枚舉到的字符和S對應位置相同則改變值T=0，否則T=1；那么有狀態轉移方程 DP[i][j] = Min{ DP[i-1][ fromstate ] + T, fromstate為所有能夠到達j的狀態 };最后DP[n][j]中的最小值就是答案。
PKU 1699 Best Sequence
題意：給定N(N <= 10)個長度不超過20的模式串，求一個長度最短的串使得它包含所有的模式串。
題解：利用模式串建立trie圖，trie圖的每個結點維護一個二進制權值，(val & 2i)不為0表示從根結點到該結點的某條路徑上有第i個模式串，用DP[i][j]表示狀態為i，模式串的二進制組合為j的最短串的長度，初始化DP[0][0] = 0，然后就轉化成了一個在trie圖上求(0, 0)到(i, 2n-1)點的最短路問題，最后求出來的DP[i][2n-1] (i < 200,
最多200個結點) 的最小值就是答案。
注意：本題中的模式串有重復的情況需要特殊處理。
HDU 2296 Ring
題意：給定N (N <= 50) 和M(M <= 100)個長度不超過10的字符串以及每個字符串的權值Hi，求一個長度不超過N的字符串使得她包含的權值最大，如果有多個解輸出長度最短的，如果還是有多個解，輸出字典序最小的。
題解：利用模式串建立trie圖，用DP[i][j]表示長度為i，處于j狀態下的字符串的最大權值，然后枚舉26個字符進行狀態轉移，轉移的過程中需要記錄每個狀態的前驅，每次進行最大值比較的時候，遇到最大值相等的情況則需要回溯，取字典序最小的。
HDU 2825 Wireless Password
題意：給定m(m <= 10)個長度不大于10的模式串，求長度為n(n <= 25)的至少包含k個模式串的字符串的種數，答案模上20090717。
題解：類似PKU
1699利用模式串建立trie圖，trie圖上每個結點表示為一個狀態，第i個模式串的權值為2i。用DP[i][j][l]表示長度為i，狀態為j，已經有t個模式串的種類數（其中l表示這t個模式串的權值的位或），那么對于每個狀態j，輸入’a-z’這26個字符后必定能夠到達下一個狀態，從DP[0][0][0]=1開始迭代計算，最終SUM
{ DP[n][j][s] , s的二進制表示中1的個數大于等于k}就是答案。
HDU 3341 Lost 's
revenge
題意：給定N(N <= 50)個長度不超過10的模式串(ACGT串)，再給定一個長度為M(M <= 40)的目標串S，求將目標串重排列，使得它包含最多的模式串，求這個最多的數目。
題解：利用模式串建立trie圖，trie圖上最多有500個結點( N*10 )，然后樸素的思想就是用S(i, iA, iC,
iG, iT)表示在i狀態下，擁有iA個A、iC個C、iG個G、iT個T的串擁有的最多的模式串的個數，但是iA, iC, iG,
iT的取值均是[0, 40]，所以我們需要把狀態壓縮一下，我們知道當四種字符都取10的時候可以讓狀態數達到最大，即114 = 14641, 所以可以令MaxA、
MaxC、MaxG、MaxT分別表示四種字符出現的個數，那么T字符的權值為1，G字符的權值為(MaxT
+ 1)，C字符的權值為(MaxG
+ 1) *(MaxT + 1)，A字符的權值為(MaxC
+ 1) *(MaxG + 1) *(MaxT + 1)，進行進制壓縮之后總的狀態數不會超過114,可以用DP[i][j]表示在trie的i號結點時ACGT四個字符個數的壓縮狀態為j時的字符串包含模式串的最多數目，然后就是進行O(4*500*114)的狀態轉移了。
HDU 2243 考研路茫茫——單詞情結
題意：給定N(N < 6)個長度不超過5的單詞，求包含至少一個單詞并且長度不超過L(L < 231)的字符串的種數。
題解：利用PKU 2778的方法構造矩陣，由于求的是長度不超過L的種數，即長度為1、2、3...L，假設原有矩陣為M，那么構造一個新的矩陣M'，它由兩個原矩陣M，一個零矩陣O和一個單位陣I構成：
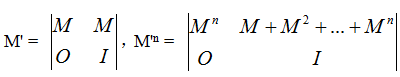該矩陣的右上角的子矩陣就是我們所求的方案矩陣，然后對 M' 二分求冪即可。這里需要總數模264，利用補碼的性質，可以直接聲明unsigned __int64直接運算即可，不需要用到大數。
HDU 3247 Resource Archiver
題意：給定n(n <= 10)個長度小于等于1000的源字符串以及m(m <= 1000)個病毒串(所有病毒串總長度不超過50000)，求一個串使得它包含所有的源字符串并且不包含任何一個病毒串，求這個字符串的最短長度(所有的串保證都是01串)。
題解：PKU 1699的加強版。
PKU 4052 Hrinity
題意：給定n(n <= 2500)個長度小于等于1100的模式串，求長度不大于5100000的目標串S中包含的模式串的數目，如果包含了模式串A和B，并且B是A的子串，那么只記錄A。
題解：建立trie圖，每個字符串結尾標記記錄模式串編號，進行目標串匹配的時候，利用哈希將所有是目標串子串的模式串標記為1，然后枚舉所有標記過的模式串，對他們進行模式匹配，利用同樣的方法將模式串的所有模式串子串標記為0，最后統計有多少個模式串的標記為1就是答案了。