王之昊在學數學
數論,組合數學,具體數學,離散數學
數論,組合數學,具體數學,離散數學
每天看8頁 計算幾何--算法與應用,在比賽前看完
每天做三道題(數學和計算幾何)
我們的隊伍只要贏,不要輸
題目
計算幾何--算法與應用
floodfill 單獨理解就是搜索,但加上離散化卻可以很好的解決一些問題
pku 1371 Tin Cutter
他就是要找到有多少個hole,floodfill用于找有多少個區間很好,
但我們必須先把圖形離散化變形成等價的形式,然后其余的就好做了
floodfill的其它題目
UVA
260 280 352 469 572 601 657 776 782 784 785 871 10267 10336 10946
pku
3338
黑書上有幅笑臉,我記得他也是有floodfill做的
今天比賽真多,凌晨1點是TCO, 中午12點又是浙大7周年慶典賽,傍晚又有sgu上petr的題。。。
1 a^p-1 = 1 mod p 和 a^p = a mod p 不等價
當 gcd(a,p) > 1時 例如 161038 2
2 浙大月賽做了兩道題,只做出一道
第一題是要知道 某個數是M的次方,而且它的第k位是 7 ,求他的最小次數
類似大數乘法
黑書上有一題是已知一個二進制數的前面一半(高位),求他可能的位數,有些不一樣,
其中在于一個是從高位考慮,一個是從低位考慮
第二題是一個關于二叉樹的,想不通為什么wa
3 sgu上的題好短,一題是問你有 n 個硬幣,告訴你他們的面值,現在要湊成 剛好 M 塊錢,不管怎么選,
有哪些硬幣是一定需要的, 感覺題目很經典,以為有什么經典算法, 但結果后來直接枚舉背包爆過了
還一題是個構造題,找找規律
摘要: 這道題顯然考察積分,但有些積分是困難的(所以要平時多做題,能判斷哪些是自己能夠手算積出來的),能積出來當然盡量算出來,但對于那些困難的,就可以模擬積分的過程, 這里微元可以選擇橫截面,對于每一個橫截面的面積 S 是 一個弓形,這是好求的,再沿軸線方向積分卻困難了,邊看代碼邊解釋:waterloo的標程 Code highlighting produced by Acti... 閱讀全文 pku 2461 Magic Bitstrings
Start by proving that in the square matrix (like the one, shown in the table in the problem statement),
the diagonal elements are always 0's if the first bit of the bitstring is 0.
這段話就可以構造出答案,猜出答案
The diagonal consists of the elements that are quadric residues modulo n. There are (n-1)/2 such distinct elements. When we mark them as 0, there are (n-1)/2 elements left. But a magic bitstring has equal number of 0's and 1's, so the remaining elements are 1.
這段話是證明猜想是對的,我還不太清楚
pku 2856 medals
仔細觀察,發現 j, k, l 太大了和 他們小的時候本質上沒什么區別,用n進制去理解,先假設 j, k, l 不相同那么只是需要三位數(n進制)就可枚舉出所有的情況 ,相同的時候用三位數(n進制)綽綽有余, 所以 用三位數就足夠枚舉了
這應該屬于幾何分布里的東西,標程的意思尚未理解
標程2
對概率太陌生,一些概率題先放這
So you want to be a 2n-aire?
Dumb Bones
Practice
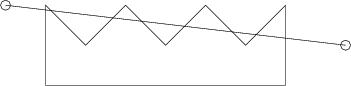
原題是求直線與多邊形的相交部分的長度
如果題中的線有了寬度 w ,那如何求他們相交部分的面積呢?
想法1:離散化
假設長直條的斜率為 l ,過多邊形每個頂點作一條斜率為 l 的直線,這些直線將多邊形離散化,
對于在長直條范圍內的單位直條進行統計,可以求得面積
題目大意是兩個城市飛機通航,航線選擇最短的球面距離,給你兩個城市的經緯度,求航線途中經過的緯度最大值是多少? 以北緯為正,南緯為負
這道題求球面坐標的方法讓人印象深刻。絕對經典。不是常見的二分,這道題Advanced Causal Measurements (ACM)是常見的二分,二分答案,
回到主題
1 經緯度的轉換是基本功Brookebond s'en va en guerre...
2 我掌握了二分圓弧的方法,管他二維還是三維的。
問題問題問題問題問題問題 問題問題問題問題問題問題 問題問題問題問題問題問題 問題問題問題問題問題問題
高斯消元
Rectilinear polygon
CDVII
Snap
Subway
Adventures in Moving - Part V
Return of the Jedi
Dumb Bones
Practice
問題問題問題問題問題問題 問題問題問題問題問題問題 問題問題問題問題問題問題 問題問題問題問題問題問題
每天做三道題(數學和計算幾何)
我們的隊伍只要贏,不要輸
題目
計算幾何--算法與應用
floodfill 單獨理解就是搜索,但加上離散化卻可以很好的解決一些問題
pku 1371 Tin Cutter
他就是要找到有多少個hole,floodfill用于找有多少個區間很好,
但我們必須先把圖形離散化變形成等價的形式,然后其余的就好做了
floodfill的其它題目
UVA
260 280 352 469 572 601 657 776 782 784 785 871 10267 10336 10946
pku
3338
黑書上有幅笑臉,我記得他也是有floodfill做的
| 名稱 | 日期 | 本星期 |
| tc SRM |
3月11號Wes | 19:00 |
| sgu&petr第四場 |
3月15號Sun | 16:00 |
| The 9th Zhejiang University Programming Contest | 3月22號 Sun | 14:00 |
| Izhevsk State Technical University Contest 3 | 3月22號 Sun | 15:00 |
今天比賽真多,凌晨1點是TCO, 中午12點又是浙大7周年慶典賽,傍晚又有sgu上petr的題。。。
1 a^p-1 = 1 mod p 和 a^p = a mod p 不等價
當 gcd(a,p) > 1時 例如 161038 2
2 浙大月賽做了兩道題,只做出一道
第一題是要知道 某個數是M的次方,而且它的第k位是 7 ,求他的最小次數
類似大數乘法
黑書上有一題是已知一個二進制數的前面一半(高位),求他可能的位數,有些不一樣,
其中在于一個是從高位考慮,一個是從低位考慮
第二題是一個關于二叉樹的,想不通為什么wa
3 sgu上的題好短,一題是問你有 n 個硬幣,告訴你他們的面值,現在要湊成 剛好 M 塊錢,不管怎么選,
有哪些硬幣是一定需要的, 感覺題目很經典,以為有什么經典算法, 但結果后來直接枚舉背包爆過了
還一題是個構造題,找找規律
摘要: 這道題顯然考察積分,但有些積分是困難的(所以要平時多做題,能判斷哪些是自己能夠手算積出來的),能積出來當然盡量算出來,但對于那些困難的,就可以模擬積分的過程, 這里微元可以選擇橫截面,對于每一個橫截面的面積 S 是 一個弓形,這是好求的,再沿軸線方向積分卻困難了,邊看代碼邊解釋:waterloo的標程 Code highlighting produced by Acti... 閱讀全文 pku 2461 Magic Bitstrings
Start by proving that in the square matrix (like the one, shown in the table in the problem statement),
the diagonal elements are always 0's if the first bit of the bitstring is 0.
這段話就可以構造出答案,猜出答案
The diagonal consists of the elements that are quadric residues modulo n. There are (n-1)/2 such distinct elements. When we mark them as 0, there are (n-1)/2 elements left. But a magic bitstring has equal number of 0's and 1's, so the remaining elements are 1.
這段話是證明猜想是對的,我還不太清楚
pku 2856 medals
仔細觀察,發現 j, k, l 太大了和 他們小的時候本質上沒什么區別,用n進制去理解,先假設 j, k, l 不相同那么只是需要三位數(n進制)就可枚舉出所有的情況 ,相同的時候用三位數(n進制)綽綽有余, 所以 用三位數就足夠枚舉了
這應該屬于幾何分布里的東西,標程的意思尚未理解
1 #include <iostream>
2 #include <cstdio>
3
4 using namespace std;
5
6 int n;
7 double d[1001], Pl, Pr;
8
9 main() {
10 while( cin >> n >> Pl >> Pr && n) {
11 d[0] = 0.0;
12 for( int i = 1; i <= n; i++ ) {
13 d[i] = 1e50;
14 for( int j = 0; j < i; j++ )
15 d[i] <?= d[j] + d[i-j-1] + 1 + // do left, right, then middle
16 (1/(1-Pl-Pr) - 1) * // E(knocking down middle)
17 ((Pl*d[j] + Pr*d[i-j-1])/(Pl+Pr) + 1);
18 // cost of knocking down middle
19 }
20 printf( "%.2lf\n", d[n] );
21 }
22 }
23
2 #include <cstdio>
3
4 using namespace std;
5
6 int n;
7 double d[1001], Pl, Pr;
8
9 main() {
10 while( cin >> n >> Pl >> Pr && n) {
11 d[0] = 0.0;
12 for( int i = 1; i <= n; i++ ) {
13 d[i] = 1e50;
14 for( int j = 0; j < i; j++ )
15 d[i] <?= d[j] + d[i-j-1] + 1 + // do left, right, then middle
16 (1/(1-Pl-Pr) - 1) * // E(knocking down middle)
17 ((Pl*d[j] + Pr*d[i-j-1])/(Pl+Pr) + 1);
18 // cost of knocking down middle
19 }
20 printf( "%.2lf\n", d[n] );
21 }
22 }
23
標程2
1 #include <math.h>
2 #include <stdio.h>
3
4 double Pl, Pr, C[1100], c; // C[m] is cost to build m in a row
5
6 int i,l,k,m,n,r;
7
8 main(){
9 while (3 == scanf("%d%lf%lf",&n,&Pl,&Pr)) {
10 if (Pl+Pr == 0) {
11 printf("%d.00\n",n);
12 continue;
13 }
14 C[0] = 0;
15 for (i=1;i<=n;i++) C[i] = 1e19;
16 for (m=1;m<=n;m++) {
17 for (l=0;l<m;l++) { // l dominoes on the left
18 r = m-l-1;
19 c = 1 + C[l] + C[r] +
20 (1/(1-Pr-Pl)-1) * (1+ Pl/(Pr+Pl)*C[l] + Pr/(Pr+Pl)*C[r]);
21 if (c < C[m]) C[m] = c;
22 }
23 }
24 printf("%0.2lf\n",C[n]);
25 }
26 }
27
2 #include <stdio.h>
3
4 double Pl, Pr, C[1100], c; // C[m] is cost to build m in a row
5
6 int i,l,k,m,n,r;
7
8 main(){
9 while (3 == scanf("%d%lf%lf",&n,&Pl,&Pr)) {
10 if (Pl+Pr == 0) {
11 printf("%d.00\n",n);
12 continue;
13 }
14 C[0] = 0;
15 for (i=1;i<=n;i++) C[i] = 1e19;
16 for (m=1;m<=n;m++) {
17 for (l=0;l<m;l++) { // l dominoes on the left
18 r = m-l-1;
19 c = 1 + C[l] + C[r] +
20 (1/(1-Pr-Pl)-1) * (1+ Pl/(Pr+Pl)*C[l] + Pr/(Pr+Pl)*C[r]);
21 if (c < C[m]) C[m] = c;
22 }
23 }
24 printf("%0.2lf\n",C[n]);
25 }
26 }
27
對概率太陌生,一些概率題先放這
So you want to be a 2n-aire?
Dumb Bones
Practice

原題是求直線與多邊形的相交部分的長度
如果題中的線有了寬度 w ,那如何求他們相交部分的面積呢?
想法1:離散化
假設長直條的斜率為 l ,過多邊形每個頂點作一條斜率為 l 的直線,這些直線將多邊形離散化,
對于在長直條范圍內的單位直條進行統計,可以求得面積
題目大意是兩個城市飛機通航,航線選擇最短的球面距離,給你兩個城市的經緯度,求航線途中經過的緯度最大值是多少? 以北緯為正,南緯為負
這道題求球面坐標的方法讓人印象深刻。絕對經典。不是常見的二分,這道題Advanced Causal Measurements (ACM)是常見的二分,二分答案,
回到主題
1 經緯度的轉換是基本功Brookebond s'en va en guerre...
2 我掌握了二分圓弧的方法,管他二維還是三維的。
問題問題問題問題問題問題 問題問題問題問題問題問題 問題問題問題問題問題問題 問題問題問題問題問題問題
高斯消元
Rectilinear polygon
CDVII
Snap
Subway
Adventures in Moving - Part V
Return of the Jedi
Dumb Bones
Practice
問題問題問題問題問題問題 問題問題問題問題問題問題 問題問題問題問題問題問題 問題問題問題問題問題問題



