HuffMan編碼
* 對給定的一組權值,實現HuffMan編碼,時間復雜度1/2n^2* 第一步:由已知的n個權值形成哈夫曼的初態
* 第二步:建立哈夫曼結點數組。依次對前面已建立的結點作如下處理
* 1. 選擇兩個權值最小且無雙親的權
* 2. 根據選出來的兩個權構造新的哈夫曼結點,修改兩個點父親結點為新建的節點
* 第三步:對哈夫曼樹進行哈夫曼編碼:從權結點逆序到根節點寫出01編碼,
然后再次逆序(正序)存儲到哈夫曼編碼數組中
1 #include<iostream>
#include<iostream>
2 #include<iomanip>
#include<iomanip>
3
4 using std::endl;
using std::endl;
5 using std::cout;
using std::cout;
6 using std::setw;
using std::setw;
7
8 const int maxlen = 10; //HuffMan編碼最大長度
const int maxlen = 10; //HuffMan編碼最大長度
9 const int MAX = 100; //比任何權重大的一個數
const int MAX = 100; //比任何權重大的一個數
10
11 struct HuffNode
struct HuffNode
12

 {
{
13 int weight;
int weight;
14 int parent;
int parent;
15 int lchild;
int lchild;
16 int rchild;
int rchild;
17 };
};
18
19 struct HuffCode
struct HuffCode
20

 {
{
21 int bit[maxlen]; //HuffMan 編碼
int bit[maxlen]; //HuffMan 編碼
22 int length; //HuffMan 編碼長度
int length; //HuffMan 編碼長度
23 int weight;
int weight;
24 };
};
25
26 void Huffman(int weight[], int n, HuffNode hn[], HuffCode hc[])
void Huffman(int weight[], int n, HuffNode hn[], HuffCode hc[])
27

 {
{
28 int i,j,l,r; //l,r分別代表新建的節點所用到的兩個結點
int i,j,l,r; //l,r分別代表新建的節點所用到的兩個結點
29 int min1,min2; //存儲每次選擇的最小的兩個權
int min1,min2; //存儲每次選擇的最小的兩個權
30
31 for(i = 0; i != 2*n - 1; ++i) //create Huffman Node,step 1
for(i = 0; i != 2*n - 1; ++i) //create Huffman Node,step 1
32

 {
{
33 if(i < n) hn[i].weight= weight[i];
if(i < n) hn[i].weight= weight[i];
34 else hn[i].weight = 0;
else hn[i].weight = 0;
35 hn[i].parent = 0;
hn[i].parent = 0;
36 hn[i].lchild = hn[i].rchild = -1;
hn[i].lchild = hn[i].rchild = -1;
37 }
}
38 for(i = 0; i != n-1; ++i) //create Huffman Node, step 2
for(i = 0; i != n-1; ++i) //create Huffman Node, step 2
39

 {
{
40 min1 = min2 = MAX;
min1 = min2 = MAX;
41 l = r = 0;
l = r = 0;
42
 /**//* 下面的一段程序本來是想直接通過輸入值確定min1,min2的初始值的,因為像上面那個MAX,不知如何給。
/**//* 下面的一段程序本來是想直接通過輸入值確定min1,min2的初始值的,因為像上面那個MAX,不知如何給。
43 但是這個代碼錯了,因為n+i-1,n+i-2不能保證其parent=0,還沒想到其他方法
但是這個代碼錯了,因為n+i-1,n+i-2不能保證其parent=0,還沒想到其他方法
44 min1 = hn[n+i-1].weight;
min1 = hn[n+i-1].weight;
45 min2 = hn[n+i-2].weight;
min2 = hn[n+i-2].weight;
46 l = n+i-1;
l = n+i-1;
47 r = n+i-2;
r = n+i-2;
48 if(min1 > min2)
if(min1 > min2)
49 {
{
50 int temp = min1;
int temp = min1;
51 min1 = min2;
min1 = min2;
52 min2 = temp;
min2 = temp;
53 int t = l;
int t = l;
54 l = r;
l = r;
55 r = t;
r = t;
56 }
}
57 */
*/
58 //find two minimum data
//find two minimum data
59 for(j = 0; j != n+i; j++)
for(j = 0; j != n+i; j++)
60

 {
{
61 if(hn[j].weight < min1 && hn[j].parent == 0)
if(hn[j].weight < min1 && hn[j].parent == 0)
62

 {
{
63 min2 = min1;
min2 = min1;
64 min1 = hn[j].weight;
min1 = hn[j].weight;
65 r = l;
r = l;
66 l = j;
l = j;
67 }
}
68 else if(hn[j].weight < min2 && hn[j].parent == 0)
else if(hn[j].weight < min2 && hn[j].parent == 0)
69

 {
{
70 min2 = hn[j].weight;
min2 = hn[j].weight;
71 r = j;
r = j;
72 }
}
73 else ;
else ;
74 }
}
75
76 //create a new Huffman Node
//create a new Huffman Node
77 hn[n+i].weight = min1+min2;
hn[n+i].weight = min1+min2;
78 hn[l].parent = n+i;
hn[l].parent = n+i;
79 hn[r].parent = n+i;
hn[r].parent = n+i;
80 hn[n+i].lchild = l;
hn[n+i].lchild = l;
81 hn[n+i].rchild = r;
hn[n+i].rchild = r;
82 }
}
83
84 int temp[maxlen]; //在此逆序存儲Huffman編碼
int temp[maxlen]; //在此逆序存儲Huffman編碼
85
86 for(i = 0; i != n; ++i)
for(i = 0; i != n; ++i)
87

 {
{
88 j = 0;
j = 0;
89 int child = i;
int child = i;
90 int parent = hn[i].parent;
int parent = hn[i].parent;
91 while(hn[child].parent != 0) //逆序存儲
while(hn[child].parent != 0) //逆序存儲
92

 {
{
93 if(hn[parent].lchild == child) temp[j++] = 0;
if(hn[parent].lchild == child) temp[j++] = 0;
94 else temp[j++] = 1;
else temp[j++] = 1;
95 child = parent;
child = parent;
96 parent = hn[parent].parent;
parent = hn[parent].parent;
97 }
}
98
99 //正序存儲到HuffCode中
//正序存儲到HuffCode中
100 int k=0;
int k=0;
101 hc[i].length = j;
hc[i].length = j;
102 hc[i].weight = weight[i];
hc[i].weight = weight[i];
103 while(j) hc[i].bit[k++] = temp[--j];
while(j) hc[i].bit[k++] = temp[--j];
104 }
}
105
106 }
}
107
108 const int N = 7;
const int N = 7;
109
110 int main()
int main()
111

 {
{
112
 int a[N] =
int a[N] =  {4,2,6,8,3,2,1};
{4,2,6,8,3,2,1};
113 HuffNode *hn = new HuffNode[2*N-1];
HuffNode *hn = new HuffNode[2*N-1];
114 HuffCode *hc = new HuffCode[N];
HuffCode *hc = new HuffCode[N];
115
116 Huffman(a,N,hn,hc);
Huffman(a,N,hn,hc);
117
118 for(int i=0; i < 2*N -1; ++i)
for(int i=0; i < 2*N -1; ++i)
119

 {
{
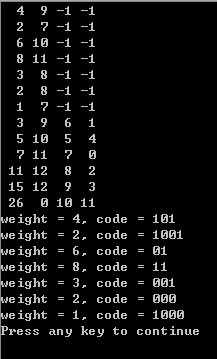
120 cout << setw(3) << hn[i].weight << setw(3) << hn[i].parent << setw(3) << hn[i].lchild << setw(3) << hn[i].rchild <<endl;
cout << setw(3) << hn[i].weight << setw(3) << hn[i].parent << setw(3) << hn[i].lchild << setw(3) << hn[i].rchild <<endl;
121 }
}
122 for(int j=0; j != N; ++j)
for(int j=0; j != N; ++j)
123

 {
{
124 cout << "weight = " << hc[j].weight << ", code = ";
cout << "weight = " << hc[j].weight << ", code = ";
125 for(int k = 0; k != hc[j].length; ++k) cout << hc[j].bit[k];
for(int k = 0; k != hc[j].length; ++k) cout << hc[j].bit[k];
126 cout << endl;
cout << endl;
127 }
}
128 return 0;
return 0;
129 }
}
 #include<iostream>
#include<iostream>2
 #include<iomanip>
#include<iomanip>3

4
 using std::endl;
using std::endl;5
 using std::cout;
using std::cout;6
 using std::setw;
using std::setw;7

8
 const int maxlen = 10; //HuffMan編碼最大長度
const int maxlen = 10; //HuffMan編碼最大長度9
 const int MAX = 100; //比任何權重大的一個數
const int MAX = 100; //比任何權重大的一個數10

11
 struct HuffNode
struct HuffNode12


 {
{13
 int weight;
int weight;14
 int parent;
int parent;15
 int lchild;
int lchild;16
 int rchild;
int rchild;17
 };
};18

19
 struct HuffCode
struct HuffCode20


 {
{21
 int bit[maxlen]; //HuffMan 編碼
int bit[maxlen]; //HuffMan 編碼22
 int length; //HuffMan 編碼長度
int length; //HuffMan 編碼長度23
 int weight;
int weight; 24
 };
};25

26
 void Huffman(int weight[], int n, HuffNode hn[], HuffCode hc[])
void Huffman(int weight[], int n, HuffNode hn[], HuffCode hc[])27


 {
{28
 int i,j,l,r; //l,r分別代表新建的節點所用到的兩個結點
int i,j,l,r; //l,r分別代表新建的節點所用到的兩個結點29
 int min1,min2; //存儲每次選擇的最小的兩個權
int min1,min2; //存儲每次選擇的最小的兩個權30

31
 for(i = 0; i != 2*n - 1; ++i) //create Huffman Node,step 1
for(i = 0; i != 2*n - 1; ++i) //create Huffman Node,step 132


 {
{33
 if(i < n) hn[i].weight= weight[i];
if(i < n) hn[i].weight= weight[i];34
 else hn[i].weight = 0;
else hn[i].weight = 0;35
 hn[i].parent = 0;
hn[i].parent = 0;36
 hn[i].lchild = hn[i].rchild = -1;
hn[i].lchild = hn[i].rchild = -1;37
 }
}38
 for(i = 0; i != n-1; ++i) //create Huffman Node, step 2
for(i = 0; i != n-1; ++i) //create Huffman Node, step 239


 {
{40
 min1 = min2 = MAX;
min1 = min2 = MAX;41
 l = r = 0;
l = r = 0;42

 /**//* 下面的一段程序本來是想直接通過輸入值確定min1,min2的初始值的,因為像上面那個MAX,不知如何給。
/**//* 下面的一段程序本來是想直接通過輸入值確定min1,min2的初始值的,因為像上面那個MAX,不知如何給。43
 但是這個代碼錯了,因為n+i-1,n+i-2不能保證其parent=0,還沒想到其他方法
但是這個代碼錯了,因為n+i-1,n+i-2不能保證其parent=0,還沒想到其他方法44
 min1 = hn[n+i-1].weight;
min1 = hn[n+i-1].weight; 45
 min2 = hn[n+i-2].weight;
min2 = hn[n+i-2].weight;46
 l = n+i-1;
l = n+i-1;47
 r = n+i-2;
r = n+i-2;48
 if(min1 > min2)
if(min1 > min2)49
 {
{50
 int temp = min1;
int temp = min1;51
 min1 = min2;
min1 = min2;52
 min2 = temp;
min2 = temp;53
 int t = l;
int t = l;54
 l = r;
l = r;55
 r = t;
r = t;56
 }
}57
 */
*/58
 //find two minimum data
//find two minimum data59
 for(j = 0; j != n+i; j++)
for(j = 0; j != n+i; j++) 60


 {
{ 61
 if(hn[j].weight < min1 && hn[j].parent == 0)
if(hn[j].weight < min1 && hn[j].parent == 0)62


 {
{63
 min2 = min1;
min2 = min1;64
 min1 = hn[j].weight;
min1 = hn[j].weight;65
 r = l;
r = l;66
 l = j;
l = j;67
 }
}68
 else if(hn[j].weight < min2 && hn[j].parent == 0)
else if(hn[j].weight < min2 && hn[j].parent == 0)69


 {
{70
 min2 = hn[j].weight;
min2 = hn[j].weight;71
 r = j;
r = j;72
 }
}73
 else ;
else ;74
 }
}75

76
 //create a new Huffman Node
//create a new Huffman Node77
 hn[n+i].weight = min1+min2;
hn[n+i].weight = min1+min2; 78
 hn[l].parent = n+i;
hn[l].parent = n+i;79
 hn[r].parent = n+i;
hn[r].parent = n+i;80
 hn[n+i].lchild = l;
hn[n+i].lchild = l;81
 hn[n+i].rchild = r;
hn[n+i].rchild = r;82
 }
}83

84
 int temp[maxlen]; //在此逆序存儲Huffman編碼
int temp[maxlen]; //在此逆序存儲Huffman編碼85

86
 for(i = 0; i != n; ++i)
for(i = 0; i != n; ++i)87


 {
{88
 j = 0;
j = 0;89
 int child = i;
int child = i;90
 int parent = hn[i].parent;
int parent = hn[i].parent;91
 while(hn[child].parent != 0) //逆序存儲
while(hn[child].parent != 0) //逆序存儲92


 {
{93
 if(hn[parent].lchild == child) temp[j++] = 0;
if(hn[parent].lchild == child) temp[j++] = 0;94
 else temp[j++] = 1;
else temp[j++] = 1;95
 child = parent;
child = parent;96
 parent = hn[parent].parent;
parent = hn[parent].parent;97
 }
}98

99
 //正序存儲到HuffCode中
//正序存儲到HuffCode中100
 int k=0;
int k=0;101
 hc[i].length = j;
hc[i].length = j;102
 hc[i].weight = weight[i];
hc[i].weight = weight[i];103
 while(j) hc[i].bit[k++] = temp[--j];
while(j) hc[i].bit[k++] = temp[--j];104
 }
}105

106
 }
}107

108
 const int N = 7;
const int N = 7;109

110
 int main()
int main()111


 {
{112

 int a[N] =
int a[N] =  {4,2,6,8,3,2,1};
{4,2,6,8,3,2,1};113
 HuffNode *hn = new HuffNode[2*N-1];
HuffNode *hn = new HuffNode[2*N-1];114
 HuffCode *hc = new HuffCode[N];
HuffCode *hc = new HuffCode[N];115

116
 Huffman(a,N,hn,hc);
Huffman(a,N,hn,hc);117

118
 for(int i=0; i < 2*N -1; ++i)
for(int i=0; i < 2*N -1; ++i)119


 {
{120
 cout << setw(3) << hn[i].weight << setw(3) << hn[i].parent << setw(3) << hn[i].lchild << setw(3) << hn[i].rchild <<endl;
cout << setw(3) << hn[i].weight << setw(3) << hn[i].parent << setw(3) << hn[i].lchild << setw(3) << hn[i].rchild <<endl;121
 }
}122
 for(int j=0; j != N; ++j)
for(int j=0; j != N; ++j)123


 {
{124
 cout << "weight = " << hc[j].weight << ", code = ";
cout << "weight = " << hc[j].weight << ", code = ";125
 for(int k = 0; k != hc[j].length; ++k) cout << hc[j].bit[k];
for(int k = 0; k != hc[j].length; ++k) cout << hc[j].bit[k];126
 cout << endl;
cout << endl;127
 }
}128
 return 0;
return 0;129
 }
}
posted on 2009-05-07 21:07 幸運草 閱讀(792) 評論(0) 編輯 收藏 引用 所屬分類: Data Structure


