均分紙牌。。。以前在做這個題目的時候，老師給了思路：就是從第一項開始加，可以讓前i堆平均為止，移動次數就是i-1了！然后繼續掃描下去！累加移動次數就是所求解！

按照這種思路，我那時直接寫了代碼完事了，其實這是很不好的！呵呵。。。雖然我們可以通過參考別人的思路解決問題，但是這我們應該更多的學習，如何從他人的解題思路里獲得自己解決類似問題的思路，如何產生思路！！！

    解題代碼一（按照老師的思路，我以前寫的）

#include<stdio.h>
int main()
{
    int  n,sum,v,sum1;
    int s[100];
    int i,j;
    int count;
     scanf("%d",&n);
    do{
        sum=0;
        sum1=0;
        v=0;
        j=0;
        count=0;
    for(i=0;i<n;i++)
    {
        scanf("%d",&s[i]);
        sum=sum+s[i];
    }

    v=sum/n;

    for(i=0;i<n;i++)
    {
        sum1=sum1+s[i];
        j=j+1;
        if((sum1%v==0)&&(sum1==v*j))
        {
            count=count+j-1;
            sum1=0;
            j=0;            
        }
    }
      printf("%d\n",count);
       scanf("%d",&n);
    }while(n!=0);
}

      今天，我又搜了一下，到底為啥是這么個解題思路，這讓我困惑了昨天一個晚上！！更可悲的是，搜出來這個題目盡然是小學生數奧里得題目。。。

      算了還是直切正題，如果有n堆紙牌要均分（當然可以均分成功），我們假設第一堆有紙牌，其他堆都沒有，那我們只要從第一推開始移動（總數-平均值）張紙牌，一堆堆往下分就解決了，這多好呀，移動次數肯定是最少的。。

      當然這只是種假設，跟多的時候是，每一堆得紙牌都有幾張，這個時候上面這種分法自然不行了，但是上面這種分法給了我們一種最少移動的思路，就是每次都把i堆分好了。。思考一下，但是新的問題又出現，不是每一堆都可以通過后一堆給（或者前一堆要）從而達到平均的，萬一后（前）一堆不夠了怎么辦？

         網上走了一遭，發現紙牌數量還可以為負！一開始我也不理解，牌數為負，就跟人可以半個沒啥兩樣，簡直就是自欺欺人！但是我回家想了下，牌數為負，固然是不對的，但是至少他在傳達著一種信息，我要牌！！！而且我要的是前i堆牌能夠達到平均值的數量，當然我們也知道，n堆紙牌是肯定能夠被平分的，就是在說最后肯定有一堆可以滿足前i堆的牌！自然他也會給他前一堆請求所需的牌，這就跟我前面舉只有第一堆有牌的情況一樣了，只是給的時候牌數不同，可見負牌其實傳達的是這種意思，而且移動次數為滿足i~j堆平分的堆數減一，即移動j-i-1次！！！于是我又寫了牌數可負的代碼：

解題代碼二如下（牌數可負）：

#include<stdio.h>
#include<string.h>
int main()
{
    int  n,sum,v;
    int s[100];
    int i,j;
    while(scanf("%d",&n)!=EOF&&n!=0)
    {
        sum=0;
        v=0;
        j=0;
        for(i=0;i<n;i++)
        {
            scanf("%d",&s[i]);
            sum=sum+s[i];
        }

        v=sum/n;

        for(i=0;i<n-1;i++)
        {
            if(s[i]<v)
            {
                s[i+1]=s[i+1]-(v-s[i]);
                j++;
            }
            else if(s[i]>v)
            {
                s[i+1]=s[i+1]+(s[i]-v);
                j++;
            }
        }
       
        
       printf("%d\n",j);
    }
    return 0;
}

寫完后我發現其實每次找到可以滿足條件的一堆牌，它都會把前面的所有堆分好！網上說這是貪心算法，但是我覺得這個貪心跟動態規劃差不多，可能還要難，因為它在動態規劃的基礎上，還要分析和總結。首先，他要找最優子結構（這個最有子結構很隱蔽），在這里找到一個找到可以給（發）牌的堆，事實上，這樣的也就找到了一個連續x堆可平分的子結構 ！其次，總結最優子結構的性質，最后發現牌數可以為負以及意義，然后發現一堆一堆往下分就是結果！最后就是老師這樣算了！！！這個過程其實很復雜。。。

 我覺得這樣還不過癮，我又寫了個這種思路下的分牌結果輸出程序，其實也可以計算移動次數（不過我覺得沒啥必要了！！）

代碼如下：

#include<stdio.h>
#include<string.h>
int temp;
void move(int i,int v,int s[100],int d[100])
{
    if(i<0||d[i]==0)    //i<0,不用解釋了，d[i]==0代表前i堆都分配好了
        return;
    if(d[i]==1)            //從后一堆拿
    {
        printf("從第%d堆紙牌向%d堆紙牌移動%d張!\n",i+1,i,v-s[i]);
        move(i-1,v,s,d);    //遞歸
        d[i]=0;                //置零，其實一次遞歸就可以讓前i堆都分配成功！
    }
    
    else if(d[i]==2)    //給后一堆
    {
        printf("從第%d堆紙牌向%d堆紙牌移動%d張!\n",i,i+1,s[i]-v);
        d[i]=0;
    }
}

//處理當前i堆函數。。。其實我自己也不知道怎么定義這個函數才對
/**//*
參數說明：
i：當前堆
v：平均值
s：堆狀態序列值
d：記錄分配情況：1代表向后一堆取，2代表向后一堆給，0代表本堆已經是平均值了，沒有操作
n：堆數
*/
void mypow(int i,int v,int s[100],int d[100],int n)
{
    if(i==n)            //前n-1堆分配成功后，第n堆一定是平均值，所以直接返回
        return;
    if(s[i]<v)            //如果本堆小于平均值，就向前一堆去要
    {
         d[i]=1;
         if(s[i+1]-(v-s[i])>=0)        //如果前一堆可以給，就直接移動,事實上這次給可以讓前i堆紙牌值全部為平均值
         {
              temp=1;
              move(i,v,s,d);        //移動函數
         }
        s[i+1]=s[i+1]-(v-s[i]);        //第i+1堆狀態變化
        mypow(i+1,v,s,d,n);            //遞歸求解i+1堆
    }
    else if(s[i]>v)                    //如果本堆大于平均值，就給后一堆
    {
        s[i+1]=s[i+1]+(s[i]-v);
        d[i]=2;
        temp=1;
        move(i,v,s,d);                //這里的move其實可以直接寫成printf
        mypow(i+1,v,s,d,n);            //遞歸求解i+1堆
    }
    else if(s[i]==v)                //如果本堆等于平均值，當然不用移動了
    {
        d[i]=0;
        mypow(i+1,v,s,d,n);            //遞歸求解i+1堆
    }
    return;
}
int main()
{
    int n,sum,v;
    int s[100],d[100];
    int i;
    int count;
    while(scanf("%d",&n)!=EOF&&n!=0)
    {
        memset(d,0,sizeof(d));
        sum=0;
        v=0;
        count=0;
        for(i=1;i<=n;i++)
        {
            scanf("%d",&s[i]);
            sum=sum+s[i];
        }

        v=sum/n;
        temp=0;
        mypow(1,v,s,d,n);
        if(!temp)                //這個就是不用分配標記
            printf("不用移動了！\n");
    }
    return 0;
}

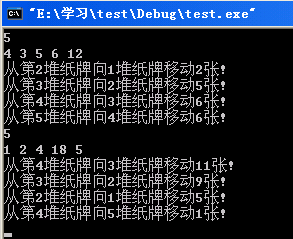
運行結果如下：