矩陣相乘問題描述:給定n個(gè)矩陣{A1,A2,...,An},當(dāng)然A1到An的任意段都是可乘的,求最小相乘次數(shù)。例如有三個(gè)矩陣維數(shù)分別為:10*100,100*2,2*5;若前兩個(gè)相乘,再乘第三個(gè),總的相乘次數(shù)=10*100*2+10*2*5=2100;若第二個(gè)與第三個(gè)先相乘,在乘第一個(gè),總相乘次數(shù)=100*2*5+10*100*5=5100;顯然,相乘次序會(huì)對(duì)計(jì)算量有很大影響,如果你在學(xué)線性代數(shù)的時(shí)候,寫了一個(gè)矩陣相乘的程序,結(jié)果跑到同學(xué)那里演示的時(shí)候,半天沒運(yùn)行出來,那就尷尬了!!!
函數(shù)調(diào)用一般會(huì)要傳參,這些參數(shù)都是非常有意義。這個(gè)題目屬于動(dòng)態(tài)規(guī)劃,最重要的一點(diǎn)就是想到一個(gè)二維數(shù)組m[i][j],代表矩陣i到矩陣j相乘的最優(yōu)解,然后就是怎樣給這個(gè)有意義的數(shù)組置數(shù)了,這種數(shù)組定義和數(shù)組置數(shù)若成,則我們要的答案就在m[1][n]中,代表矩陣1到矩陣n相乘的最優(yōu)解。(如果你很饑渴的想解決這個(gè)問題,就直接看代碼吧!!)有人可能會(huì)問,為什么會(huì)想到這種數(shù)組定義,主要有兩個(gè)方面:一,學(xué)習(xí)(高效),看多了自然會(huì)想到給數(shù)組某種意義,培育一種思想;二、思考與分析,來的緩慢,但是凌駕與學(xué)習(xí)之上,也是學(xué)習(xí)的目的,是終極武器,也是基礎(chǔ)武器。。。。
不扯了,回到主題,很明顯如果只有一個(gè)矩陣,相乘次數(shù)為零;如果有兩個(gè),直接相乘,若第一個(gè)矩陣維數(shù)q*p,第二個(gè)矩陣維數(shù)p*r,相乘次數(shù)為q*p*r;三個(gè)矩陣相乘,為前兩相乘,再乘第三個(gè),和后兩個(gè)先相乘,再乘第一個(gè),取其優(yōu)者;四個(gè)矩陣相乘,設(shè)第三個(gè)矩陣維數(shù)r*t,第四個(gè)矩陣t*k,維數(shù)min{前三個(gè)矩陣最優(yōu)值+q*t*k,前兩個(gè)矩陣最優(yōu)+后兩個(gè)矩陣最優(yōu)+q*r*k,前一個(gè)矩陣最優(yōu)+后三個(gè)矩陣最優(yōu)+q*p*k};然后。。。
有人可能會(huì)問:我可以算出前一個(gè),前兩個(gè),前三個(gè)矩陣相乘的最優(yōu),但是我怎么算出后一個(gè),后兩個(gè),后三個(gè)相乘的最優(yōu)呢?
其實(shí)這個(gè)問題又回到了原點(diǎn),這就是動(dòng)態(tài)規(guī)劃的妙處,顯然我們先求出A1到An的任意段長度為2矩陣的最優(yōu)(直接相乘),然后可以計(jì)算出任意段長度為3矩陣的最優(yōu);然后。。。然后我們就想了個(gè)m[i][j]出來,記錄我們求的的結(jié)果;然后再寫代碼,嘗試思想的準(zhǔn)確性,當(dāng)然我們更多的時(shí)候是站在先人的肩膀上做驗(yàn)證工作。。。
代碼如下(參考教科書):
 #include<iostream>
#include<iostream>
 using namespace std;
using namespace std;
 void chain(int *p,int n,int m[][7],int s[][7])//p維數(shù)數(shù)組,m最優(yōu)乘次數(shù)組,s記錄劃分方案
void chain(int *p,int n,int m[][7],int s[][7])//p維數(shù)數(shù)組,m最優(yōu)乘次數(shù)組,s記錄劃分方案


 {
{
 int j;
int j;
 for(int i=1;i<=n;i++)
for(int i=1;i<=n;i++)
 m[i][i]=0;
m[i][i]=0;
 for(int r=2;r<=n;r++)
for(int r=2;r<=n;r++)


 {
{
 for(i=1;i<=n-r+1;i++)
for(i=1;i<=n-r+1;i++)


 {
{
 j=i+r-1;
j=i+r-1;
 m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];
 s[i][j]=i;
s[i][j]=i;
 for(int k=i+1;k<j;k++)
for(int k=i+1;k<j;k++)


 {
{
 int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
 if(t<m[i][j])
if(t<m[i][j])


 {
{
 m[i][j]=t;
m[i][j]=t;
 s[i][j]=k;
s[i][j]=k;
 }
}
 }
}
 }
}
 }
}
 for(i=1;i<=n;i++) //我把它翻過來輸出。。。
for(i=1;i<=n;i++) //我把它翻過來輸出。。。


 {
{
 for(j=n;j>=i;j--)
for(j=n;j>=i;j--)


 {
{
 cout<<m[i][j]<<' ';
cout<<m[i][j]<<' ';
 }
}
 cout<<endl;
cout<<endl;
 }
}

 }
}

 void Traceback(int i,int j,int s[][7]) //輸出相乘方案
void Traceback(int i,int j,int s[][7]) //輸出相乘方案


 {
{
 if(i==j)
if(i==j)
 return;
return;
 Traceback(i,s[i][j],s);
Traceback(i,s[i][j],s);
 Traceback(s[i][j]+1,j,s);
Traceback(s[i][j]+1,j,s);
 cout<<"Multiply A "<<i<<","<<s[i][j];
cout<<"Multiply A "<<i<<","<<s[i][j];
 cout<<" and B "<<(s[i][j]+1)<<","<<j<<endl;
cout<<" and B "<<(s[i][j]+1)<<","<<j<<endl;
 return;
return;
 }
}
 int main()
int main()


 {
{
 int p[7],m[7][7],s[7][7],n;
int p[7],m[7][7],s[7][7],n;
 while(scanf("%d",&n)!=EOF)
while(scanf("%d",&n)!=EOF)


 {
{
 for(int i=0;i<=n;i++)
for(int i=0;i<=n;i++)


 {
{
 scanf("%d",&p[i]);
scanf("%d",&p[i]);
 }
}
 chain(p,n,m,s);
chain(p,n,m,s);
 Traceback(1,6,s);
Traceback(1,6,s);
 }
}
 return 0;
return 0;
 }
}

 /**//*
/**//*
 p52
p52
 測試數(shù)據(jù):
測試數(shù)據(jù):
 6
6
 30 35 15 5 10 20 25
30 35 15 5 10 20 25
 */
*/

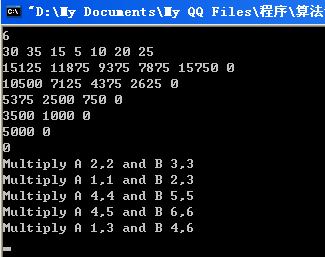
運(yùn)行結(jié)果:
posted on 2010-09-04 11:53
jince 閱讀(2555)
評(píng)論(0) 編輯 收藏 引用 所屬分類:
算法設(shè)計(jì)與分析