我編寫的第一個JAVA程序，在Eclipse上成功運行！發博文表示慶賀，向Java處理大整數進發……
public class main{
public static void main(String[] args) {
System.out.println("Hello");
}
}
雖然Java里面有很多知識，目前對于我來說都是未知，但只要一步步努力，一點點進步，菜鳥起飛啦！
附上一篇文章：
JAVA大數處理(BigInteger,BigDecimal) 今日見了一個名詞
SDK（Software Development Kit, 即軟件開發工具包 ）
posted @
2010-10-07 21:08 孟起 閱讀(219) |
評論 (0) |
編輯 收藏
把在n條線段中（以（0,0）為起點）放入m個點，使其等分為m+1份。
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3414
#include<stdio.h>
#include<math.h>
struct point
{
double x,y,len;
}p[1002];
int main()
{
int n,m,i,j,ca=1;
double ave,len,ax,ay;
while(scanf("%d%d",&n,&m)!=EOF)
{
p[0].x=0; p[0].y=0; ave=0;
for(i=1;i<=n;i++){
scanf("%lf%lf",&p[i].x,&p[i].y);
p[i].len=sqrt((p[i].x-p[i-1].x)*(p[i].x-p[i-1].x)+(p[i].y-p[i-1].y)*(p[i].y-p[i-1].y));
//printf("%.3f %.3f %.3f\n",p[i].x,p[i].y,p[i].len);
ave+=p[i].len;
}
ave/=(m+1); //每一份的均長
j=0; //沿著線段走
// printf("%.3f\n",ave);
printf("Route %d\n",ca++);
for(i=1;i<=m;i++)
{
len=0;
for(; j<n;j++)
{
if(len+p[j+1].len>ave)
break;
len+=p[j+1].len;
}
double res=ave-len;
//printf("%d %.3f\n",j,res);
ax=p[j].x+(res/p[j+1].len)*(p[j+1].x-p[j].x);
ay=p[j].y+(res/p[j+1].len)*(p[j+1].y-p[j].y);
printf("CP%d: (%.3lf, %.3lf)\n",i,ax,ay);
p[j].x=ax; p[j].y=ay;
p[j+1].len=sqrt((p[j+1].x-p[j].x)*(p[j+1].x-p[j].x)+(p[j+1].y-p[j].y)*(p[j+1].y-p[j].y));
}
}
return 0;
}posted @
2010-10-07 18:25 孟起 閱讀(352) |
評論 (0) |
編輯 收藏一個環形的圈怎樣用最少次數把它從順時針變成逆時針（只能相鄰位置交換位置）
一個環形，最優結果是把這個環分成 相差 最少的2部分，這2部分按照直線來求出結果再求和
直線如果把1234 換成4321
是冒泡的次數。。首先4123（3）+4312（2）+4321（1）=6
本題是把n看成兩個 n/2 ，然后求出進行反序（冒泡）的次數
#include <stdio.h>
int main()
{
int n,t,r;
while(scanf("%d",&n)!=EOF)
{
t=n/2; r=n-t;
printf("%d\n",t*(t-1)/2+r*(r-1)/2);
}
return 0;
}
posted @
2010-10-07 10:10 孟起 閱讀(738) |
評論 (0) |
編輯 收藏解決一個問題通常有多種方法， 我們總想找到最高效的，所以需要對比不同算法執行所用的時間。可惜的是，C++中提供的方法一般只能精確到毫秒級。
提供一種更加精確的方法。編寫一個函數，可以在C++中這樣寫：
__declspec (naked) unsigned __int64 GetCpuCycle( void )
{
_asm
{
rdtsc
ret
}
}
RDTSC的返回值存放在EDX EAX中， EDX為高32位，EAX為低32位。這里的 RDTSC 指令( Read Time Stamp Counter )， 獲得CPU的高精度時間戳。
這樣以來我們就可以在隨處獲得當前的CPU自上電以來的時間周期數了：
unsigned __int64 iCpuCycle = GetCpuCycle();
根據這個數字我們可以計算出上電以來所經歷的時間( 秒s )：
second = iCpuCycle / CPU主頻率( HZ );
1GHZ = 1,000 MHZ = 1,000,000 KHZ = 1,000,000,000 HZ;
獲取兩次作差就可以得到運行的時間了。其實沒必要換算成時間，關注差值就行了。
PS：
可以放心一個unsigned __int64 不會溢出 - - 可以計算一下你的CPU能保存多少年的時間。。
根據這一方法有幾個好處： 一是精度高，二是函數調用開銷最小，三是平臺限制小，四是具有和CPU主頻相對應的直接關系。。。 但是由于精度高，得到的數字浮動比較大。。
posted @
2010-10-06 21:39 孟起 閱讀(682) |
評論 (0) |
編輯 收藏A triangle field is numbered with successive integers in the way shown on the picture below.
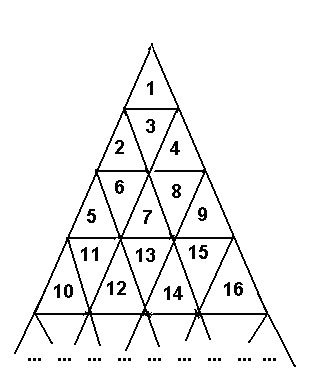
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.
Write the program to determine the length of the shortest route connecting cells with numbers N and M.
#include <stdio.h>
#include<math.h>
int main()
{
int temp,n,m,s,flag=3,cn,cm,zb,yb,cc,k,sj;
while(scanf("%d%d",&m,&n)==2 )
{
flag=3; s=0; k=0;
if(m>n)
{
temp=m; m=n; n=temp;
}
cn=(int)ceil(sqrt(n)); //判斷n和m所在層數
cm=(int)ceil(sqrt(m));
cc=abs(cn-cm); //判斷兩點層差
zb=m+(cn-1)*(cn-1)-(cm-1)*(cm-1); //判斷m輻射到n層所及范圍的左邊界和右邊界
yb=zb+2*cc;
if(n>=zb && n <=yb) //判斷n在m范圍所須步數
{
s=2*(cc);
k=1;
}
else
{
if(n<zb) //判斷n到m邊界及m點所須步數和
s=2*(cc)+abs(n-zb);
else
s=2*(cc)+abs(n-yb);
}
sj=m-(cm-1)*(cm-1); //判斷三角類型0正,1倒
if(abs(n-m)% 2 !=(cc) % 2)
{
if(sj % 2 ==1 )
flag=1;
else
flag=0;
}
if(flag==1 && k==1)
s=s-1; //假如n點在m點輻射范圍內,正三角-1,倒三角+1,不在不判斷.
if(flag==0 && k==1)
s=s+1;
printf("%d\n",s);
}
return 0;
}
cn-1)*(cn-1)是1到n-1行末尾的數，也就是1-n的里面小三角形的個數~，
(cm-1)*(cm-1);也是一樣的嘛~
兩個相減就是m行的個數了！~ m加個數不就是左邊界了嘛~
zb+兩倍的行差就是右邊界了！~
而且正三角所到的邊界是正三角型，反三角所到的邊界是反三角型，這點要注意！
posted @
2010-10-06 18:05 孟起 閱讀(1317) |
評論 (1) |
編輯 收藏http://acm.hdu.edu.cn/showproblem.php?pid=1875
Kruscal最小生成樹 注意對double類型的快排可不要寫錯了
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
struct road{
int x,y;
double v;
}r[5002];
struct point{
int a,b;
}p[102];
int cmp(const void *a,const void *b)
{
struct road *aa=(struct road *)a;
struct road *bb=(struct road *)b;
return aa->v > bb->v ? 1:-1;
}
int bin[102];
int find(int x)
{
int r=x;
while(bin[r]!=r)
r=bin[r];
int y=x;
while(bin[y]!=y)
{
y=bin[y];
bin[y]=r;
}
return r;
}
int main()
{
int t,n,i,j,num,cnt;
double ans;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=0;i<n;i++)
scanf("%d%d",&p[i].a,&p[i].b);
num=0;
for(i=0;i<n-1;i++)
for(j=i+1;j<n;j++){
r[num].x=i, r[num].y=j;
r[num].v=sqrt(1.0*(p[i].a-p[j].a)*(p[i].a-p[j].a)+(p[i].b-p[j].b)*(p[i].b-p[j].b));
num++;
}
for(i=0;i<n;i++)
bin[i]=i;
qsort(r,num,sizeof(r[0]),cmp);
i=0; ans=0; cnt=0;
while(r[i].v<10)
i++;
for(;i<num && cnt<n-1;i++)
{
if(r[i].v>1000) break;
int fx=find(r[i].x), fy=find(r[i].y);
if(fx!=fy)
{
bin[fx]=fy;
cnt++;
ans+=r[i].v;
}
}
if(cnt==n-1)
printf("%.1lf\n",ans*100);
else
printf("oh!\n");
}
return 0;
}
posted @
2010-10-06 10:26 孟起 閱讀(580) |
評論 (0) |
編輯 收藏
最簡單的dijkstra應用，別的就不說了 題目鏈接：
http://acm.hdu.edu.cn/showproblem.php?pid=1874
#include<stdio.h>
#include<string.h>
#define MAXN 201
#define MAX 999999
int dist[MAXN][MAXN],x[MAXN];
int main()
{
int n,m,i,j,t,s,d,a,b,time,min;
while(scanf("%d%d",&n,&m)==2)
{
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
if(i==j)
dist[i][j]=0;
else
dist[i][j]=MAX;
}
}
for(i=0;i<m;i++)
{
scanf("%d%d%d",&a,&b,&time);
dist[a][b]=dist[b][a]=time<dist[a][b]?time:dist[a][b];
}
scanf("%d%d",&s,&d);
for(i=0;i<n;i++)
x[i]=dist[s][i];
dist[s][s]=1;
t=0;
while(t!=-1)
{
min=-1;
t=-1;
for(i=0;i<n;i++)
if(dist[i][i]==0&&(min==-1||x[i]<min))
{
min=x[i];
t=i;
}
if(t!=-1)
{
dist[t][t]=1;
for(i=0;i<n;i++)
if(x[i]>x[t]+dist[t][i])
{
x[i]=x[t]+dist[t][i];
}
}
}
if(x[d]<MAX)
printf("%d\n",x[d]);
else
printf("-1\n");
}
return 0;
}
posted @
2010-10-06 09:23 孟起 閱讀(542) |
評論 (0) |
編輯 收藏
思路如下，只要房子的號碼是個完全平方數就可以逃跑了。
為什么呢？？？
因為完全平方數比方是25，只能分解為1，5，25，這三個數，以1代表門開了，0代表關了，則此時的序列就是1，0，1，
所以只要對輸入的數求下平方根就好了。
換句話說在區間[1,n]中能整除n的數的個數，當n是平方數是奇數個，否則是偶數個。
http://acm.hdu.edu.cn/showproblem.php?pid=1337
#include<stdio.h>
#include<math.h>
int main()
{
int n,a;
scanf("%d",&n);
while(n--)
{
scanf("%d",&a);
printf("%d\n",(int)sqrt(a*1.0));
}
return 0;
}
posted @
2010-10-05 20:07 孟起 閱讀(593) |
評論 (0) |
編輯 收藏在一無限大的二維平面中，我們做如下假設：
1、 每次只能移動一格；
2、 不能向后走（假設你的目的地是“向上”，那么你可以向左走，可以向右走，也可以向上走，但是不可以向下走）；
3、 走過的格子立即塌陷無法再走第二次；
求走n步不同的方案數（2種走法只要有一步不一樣，即被認為是不同的方案）。
http://acm.hdu.edu.cn/showproblem.php?pid=2563
1 /*設a[n]是向上走n步的方法數，b[n]是向左或向右走的方法數，
2 則a[n]=a[n-1]+b[n-1], b[n]=２*a[n-1]+b[n-1]
3 因為f[n]=a[n]+b[n]
4 化簡得f[n]=3*a[n-1]+2*b[n-2]=2*f[n-1]+a[n-1]=2*f[n-1]+f[n-2]
5 */
6 #include<stdio.h>
7 int main()
8 {
9 int i,t,n,f[22];
10 f[1]=3; f[2]=7;
11 for(i=3;i<=20;i++)
12 f[i]=2*f[i-1]+f[i-2];
13 scanf("%d",&t);
14 while(t--)
15 {
16 scanf("%d",&n);
17 printf("%d\n",f[n]);
18 }
19 return 0;
20 }
posted @
2010-10-05 11:54 孟起 閱讀(633) |
評論 (0) |
編輯 收藏