Euler的任意四面體體積公式（已知邊長求體積）

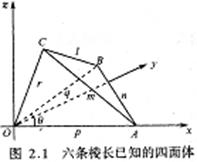
已知4點(diǎn)坐標(biāo)求體積（其中四個(gè)點(diǎn)的坐標(biāo)分別為（x1,y1,z1）,（x2,y2,z2）,（x3,y3,z3）,（x4,y4,z4）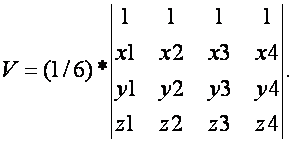

注意事項(xiàng)：

1. 注意舍入方式(0.5的舍入方向);防止輸出-0.

2. 幾何題注意多測試不對稱數(shù)據(jù).

3. 整數(shù)幾何注意xmult和dmult是否會(huì)出界;

   符點(diǎn)幾何注意eps的使用.

4. 避免使用斜率;注意除數(shù)是否會(huì)為0.

5. 公式一定要化簡后再代入.

6. 判斷同一個(gè)2*PI域內(nèi)兩角度差應(yīng)該是

   abs(a1-a2)<beta||abs(a1-a2)>pi+pi-beta;

   相等應(yīng)該是

   abs(a1-a2)<eps||abs(a1-a2)>pi+pi-eps;

7. 需要的話盡量使用atan2,注意:atan2(0,0)=0,

   atan2(1,0)=pi/2,atan2(-1,0)=-pi/2,atan2(0,1)=0,atan2(0,-1)=pi.

8. cross product = |u|*|v|*sin(a)

   dot product = |u|*|v|*cos(a)

9. (P1-P0)x(P2-P0)結(jié)果的意義:

   正: <P0,P1>在<P0,P2>順時(shí)針(0,pi)內(nèi)

   負(fù): <P0,P1>在<P0,P2>逆時(shí)針(0,pi)內(nèi)

   0 : <P0,P1>,<P0,P2>共線,夾角為0或pi