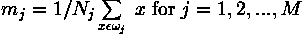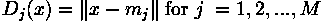楊健老師的論文KPCA Plus LDA: A Complete Kernel Fisher Discriminant Framework for Feature Extraction and Recognition 5.1節(jié)采用該分類器，Why can LDA be performed in PCA transformed space也采用該分類器，等同于葉杰平老師論文Generalized Linear Discriminant Analysis: A Unified Framework and Efficient Model Selection IV節(jié)的nearest-centroid classifier（也即汪增福老師講的平均樣本法），定義如下：（摘自網(wǎng)頁
http://homepages.inf.ed.ac.uk/rbf/HIPR2/classify.htm）
Suppose that each training class is represented by a prototype (or mean) vector:
where 
is the number of training pattern vectors from class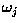 
. In the example classification problem given above, 
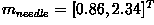and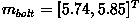 
as shown in Figure 2.
Figure 2 Feature space: + sewing needles, o bolts, * class mean
Based on this, we can assign any given pattern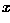 
to the class of its closest prototype by determining its proximity to each 
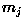. If Euclidean distance is our measure of proximity, then the distance to the prototype is given by
It is not difficult to show that this is equivalent to computing
and assign 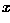to class 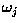if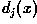 
yields the largest value.
顯然，minimum distance classifier的效率要比nearest neighbor classifier (NN)要低，因為對于任意一個測試樣本，前者只需要計算到訓(xùn)練樣本的幾個類心的距離，而nearest neighbor classifier (NN)要計算與所有訓(xùn)練樣本的距離。楊健老師論文KPCA Plus LDA 5.2節(jié)也有原話：A minimum distance classifier is employed for computational efficiency.
Other reference:
Mar 24, 2012 gmail 附件講義7.3節(jié)有minimum distance classifier的英文描述