單鏈表的快速排序
單鏈表的快速排序跟數(shù)組的排序原理上一致，有一個分區(qū)（區(qū)分）的函數(shù)在一個區(qū)間中針對某個標(biāo)桿值進(jìn)行區(qū)分，比它大的放它后面，比它小的放它前面，并返回它的地址，好對它前面的以及它后面的遞歸。
單鏈表的快速排序跟數(shù)組有個明顯的區(qū)別，就是指示起始和終止的元素，在一輪之后它們在鏈表中的位子會發(fā)生改變，所以需要返回一個新的起始的位置（終止的位置）
我的算法中總是拿后一個的節(jié)點作為終止位置，所以它在鏈表中的位子其實是不改變的，所以我只修改了起始位置指向新的起始位置即可。
我的算法是，用2個鏈表，一個放比它大的一個放比它小的，最后接起來，它的位置就是mid，而其實位置就是當(dāng)初起始的前一個節(jié)點在新鏈表中的next。有點拗口，就是說a->start->...->nullptr，這一輪傳進(jìn)來的是start，那么經(jīng)過這輪的分區(qū)之后，start的位置肯定改變了，對吧？但是a->next的地址沒有改變，即&(a->next)，因為start之前的都會原封不動的放在那里。我覺得用指針的地址來處理是這里的關(guān)鍵之處吧。
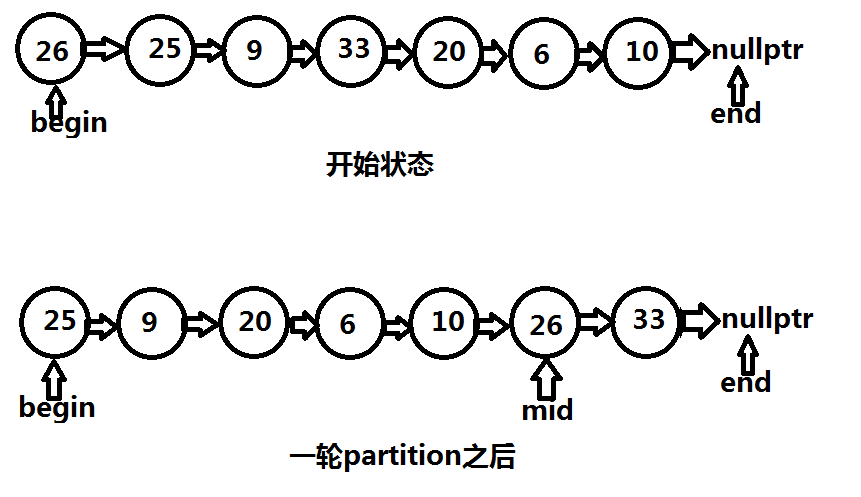
這是一輪partition之前和之后的圖示，之后就對于(begin, mid)和（mid->next, end)進(jìn)行快速排序即可。
1 // Problem: sort a singly link list by Quick Sort
2 node *partition(list &l, node *&begin, node *end = nullptr) {
3 // if end is the next node, that means it's only one node to sort
4 if (begin == nullptr || end == begin->next) {
5 return nullptr;
6 }
7
8 list small_list, big_list;
9 node *current = l.root;
10 node *pivot = begin;
11 node **pbegin; // points to the address of begin
12 node **s_current = &small_list.root, **b_current = &big_list.root;
13
14 // move previous nodes before 'begin' to small list
15 while (current != begin) {
16 *s_current = current;
17 s_current = &(*s_current)->next;
18 current = current->next;
19 }
20
21 // pbegin presents the location(address) of begin item, e.g. if (a->next == begin) then pbegin = &a->next;
22 pbegin = s_current;
23
24 while (begin != end) {
25 if (begin->data < pivot->data) {
26 *s_current = begin;
27 s_current = &(*s_current)->next;
28 }
29 else {
30 *b_current = begin;
31 b_current = &(*b_current)->next;
32 }
33
34 begin = begin->next;
35 }
36
37 // pass begin back to quick_sort for next sort action
38 begin = *pbegin;
39
40 *b_current= end;
41 *s_current = big_list.root;
42 l = small_list;
43 l.print();
44
45 // current pivot would be the end node for smaller set sorting
46 return big_list.root;
47 }
48
49 void quick_sort(list &l, node *begin, node *end = nullptr) {
50 if (begin == end) {
51 return;
52 }
53 // mid represents the pivot node which is the next node of the end of the small list
54 node *mid = partition(l, begin, end);
55
56 if (mid != nullptr){
57 quick_sort(l, begin, mid);
58 }
59
60 if (mid != nullptr &&
61 mid->next != nullptr) {
62 quick_sort(l, mid->next, end);
63 }
64 }
代碼