Posted on 2006-09-02 21:16
chenger 閱讀(703)
評論(0) 編輯 收藏 引用 所屬分類:
Programming Stuff

主要是因為看了
這篇blog突然想到的。這個篩法求素數(shù)的程序想必每個學編程的人都寫過,幾乎是最經(jīng)典的算法之一了,雖然似乎沒什么用。但好像的確沒見過對這個古老算法的嚴格分析。一時好奇,就想把這個算法納入大O的框架之中……不管怎么樣,先拿出代碼再說
require'benchmark'
?
def sievePerformance(n)
??? r = Benchmark.realtime() do
??????? sieve = Array.new(n,true)
??????? sieve[0..1] = [false,false]
??????? 2.upto(n) do |i|
??????????? if sieve[i]
??????????????? (2*i).step(n,i) do |j|
??????????????????? sieve[j] = false
??????????????? end
??????????? end
??????? end
??? end
??? r
end這段代碼抄自前面Robert C.Martin先生的blog,對篩法作性能測試。初看起來,程序的主體是二重循環(huán),因此算法的復雜性好像是O(N
2)之類的玩意?要么是O(NlnN)?
?
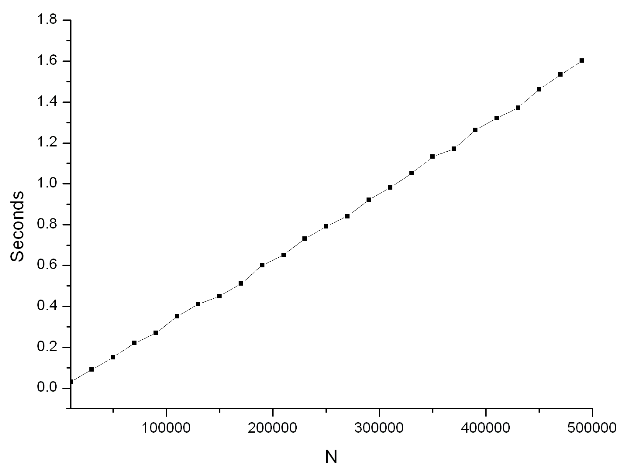
下圖是Ruby自帶的benchmark模塊測量的結(jié)果,上限N從10000到500000,步長20000。Rober C.Martin的文章里也有一張圖,是從1000000到5000000,從圖中可以看到,他電腦的性能遠勝于我,我要是從1000000到5000000這么跑一遍,花兒都謝了……總之,實測的結(jié)果是:這個算法的性能基本上是線性的。出于對ruby這樣的解釋型語言的某種不信任,我又把這段程序用C++重寫了一遍,拿C標準庫提供的clock函數(shù)測量時間,結(jié)果在N小于10000000的時候,基本上呈線性,但再往后花費的時間就開始超過線性增長了。
下面我給一個比較粗略的分析,解釋為什么這個算法的復雜度表現(xiàn)為線性。首先,我認為主要花費時間的是對sieve數(shù)組的讀寫,循環(huán)變量的增加應該可以忽略。如果p<N是素數(shù),那么就要進入內(nèi)循環(huán)將i的倍數(shù)“挖掉”,也就是對sieve的相應元素賦值,要進行[N/p]-1次。這樣就得到總共的賦值次數(shù)S為:
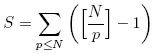
其中p為素數(shù)。顯然
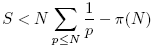
數(shù)論中有個Mertens定理可以估計上面括號中的和式,結(jié)果為
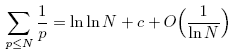
其中c是一個常數(shù)。可以看到,在N很大時和式的主要部分為NlnlnN。而lnlnN是一個增長極慢的函數(shù),lnln10
5=2.44,lnln10
9=2.91,幾乎就可以當常數(shù)處理(至少在32位無符號整數(shù)范圍內(nèi))。其他的一些項,比如循環(huán)變量的步進,都是O(N),這也就不難理解整個程序的性能是幾乎是O(N)了。
Update:上面的代碼有個很明顯的問題,就是內(nèi)循環(huán)應該從i*i開始,而不是2*i,這樣對于比較大的N,性能提高很明顯(接近一半)。另外一個可改進的地方是外層循環(huán)的upto(n),可以改為upto(Integer(Math.sqrt(n)),其實這兩個改動效果是重疊的,任意改一個就差不多了。賦值次數(shù)S應為:
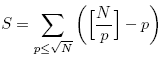
結(jié)果為:
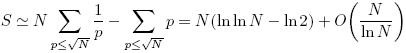
可以看到效率的提升是很明顯的,畢竟lnln2
32也才不到3.1,ln2約為0.7。