欧美精品九九99久久在观看,久久久久99精品成人片三人毛片 ,久久亚洲av无码精品浪潮

g++的一个bug?

chenger — Thu, 12 Oct 2006 08:28:00 GMT

今天写代码的时候，发现g++好像不支持模板成员函数的全特化。看代码�Q?br />
class A
{
public:
    template <typename T>
    T f(T val);

    template <>
    int f<int>(int val);
};

我用的是g++ 3.4.2 mingw版本。编译上面这�D�代码时�Q�错误信息如下：

5: error: invalid explicit specialization before '>' token
5: error: explicit specialization in non-namespace scope `class A'

如果把f的定义放到全局作用域中�Q�就不会出错。而上面这�D�代码在VC++ 8.0下可以编译通过。运行�v来也没有问题。别的编译器我没有试�q��?br />
Update�Q�多谢周星星的指点，比较“常规”的写法如下:

class A
{
public:
    template <typename T>
    T f(T val);
};

template <typename T>
T A::f(T val)
{
    // ...
}

template <>
int A::f<int>(int val)
{
    //...
}

�q�种写法��没有�Q何问�?在g++ 3.4.2和VC++ 8.0下均表现正常�Q�。至于�ؓ什么前面的写法��D��g++下报错，�q�不是很清楚�?img src ="http://www.shnenglu.com/chengmeng/aggbug/13604.html" width = "1" height = "1" />

chenger 2006-10-12 16:28 发表评论

Exploring Ruby I:Name Conventions

chenger — Fri, 29 Sep 2006 10:56:00 GMT

Ruby中的名字�U�定

历史�Q�高�U�程序语�a�的老祖宗，Fortran�Q�对源程序中的名字，或者叫标识�W?identifier)有很严格的规定，譬如首字母代表变量的�c�d��{�等。个��是当�q�编译技术还未成熟时的权宜之计。后来主��的�E�序设计语言都放松了对名字的限制�Q�像C/C++/Java�Q�只有一点点��小的约束（�Ҏ��用字�W�的限制�Q�只能��用英文字母、数字、下划线�Q�必��M��下划�U�或英文字母开头。这也容易理解，完全是�ؓ了写词法分析器的方便�Q�。而和Fortran同时代的Lisp�Q�这斚w��更是大开�l�灯�Q�爱怎么定义怎么定义。然而到了现在，��g��有点复古的潮��，有些语言开始对名字讄��一些规则，比如Haskell,Erlang,包括Ruby�?br />
�a�归正传。Ruby中的名字规则主要是根据名字的�W�一个字母来军_��q�个名字的��用方式。具体来��_��

局部变量，�Ҏ��名，�Ҏ��参数�Q�以��写字母或下划线开��_��?_'�q�接�?br />Example�Q�i,note_controller
帔R��Q�全部大写，�?_'�q�接
Example�Q�A_NUM
�c�，模块(module)�Q�都是开头大写（因�ؓ�c�d��是全局变量�Q�，其他��写�q�且直接�q�接在一�?br />Example�Q�ActiveRecord
全局变量�Q�以'$'开��_��肯定是跟Perl学的�Q�我觉得不怎么好）
实例变量(instance variable)�Q�以'@'开��_��同上�Q?/li>
�c�d��?class variable)�Q�以'@@'开��_��诡异�Q?/li>

有点Perl的味道，但Perl更加变态，居然要以首字母区分标量、数�l�和Hash表，�q�就不太人道了。相比�v来，Ruby的设�|�还是可以接受的�Q�它只不�q�是把有些约定俗成的规则直接变成了语�a�规则。每个程序员基本上都会有自己的一套命名规则，比如写C++�E�序�Ӟ��c�d��通常用大写字母开��_��宏名则通常由大写字母组成，而下划线开头的�Q�特别是双下划线�Q�往往留给库开发者等�{�。Ruby的想法可能是�Q�干脆统一了这些命名规则，免得��Z��U�风�?Style)问题争论不休。也是挺有道理的�?img src ="http://www.shnenglu.com/chengmeng/aggbug/13156.html" width = "1" height = "1" />

chenger 2006-09-29 18:56 发表评论

玩了玩Ruby

chenger — Sun, 24 Sep 2006 06:50:00 GMT

我在自己的电脑上装了ruby�Q�稍微看了点Programming Ruby�Q�感觉Ruby有很多想法都非常有意思，值得学习�Q�比如块�Q�以及彻底的Object Oriented(对于谁比谁更OO�Q�从来都是争吵不断，比如Java比C++更OO�Q�C#比Java又更OO�Q�等�{�，往往引�v论坛上一片腥风血雨。我�q�个也就是随便说��_��Q��P代器。很多语�a��Ҏ��和Python相差不大�Q�估计脚本语�a�做到一定程度多��都有些�怼�的，当然各有各的特点。然后又看了�Ҏ��代码�Q�终于明白�ؓ何Ruby的性能如此被�h诟病�Q�构造了AST以后�Q�直接在AST上递归�q�行eval。而Python�Q�Perl,Lua�{�都是编译�ؓ中间语言再交�l�虚拟机执行。如果能有一个JIT�~�译器（�?NET那样�Q�就更牛了。Ruby传说中的2.0版本要引入虚拟机�Q�YARV。不�q�那2.0遥遥无期�Q�目前最新的stable�?.8.5�Q?.0据说要到08奥运那会了�?br />
Ruby的源代码�q�充分体��C��拿来��M��的精��，能重用的决不自己写：比如Hash表就用了一个通用的Hash表实玎ͼ�正则表达式则使用了GNU的regex库，random是有名的MT19937�Q�也是日本�h写的�Q�。尝试了一下编译，在mingw上执行标准三部曲�Q?/configure,make,make install�Q�一切OK�?br />

chenger 2006-09-24 14:50 发表评论

Google面试题之补充

chenger — Sat, 16 Sep 2006 07:35:00 GMT

上次写了一��关于google面试题的文章。我�l�的��法跑得很慢�Q�后面张沈鹏同学用python写了一�?a href="/zuroc/archive/2006/09/16/12540.html">��法�Q�速度很快�Q�再�ơ感觉python的性能不像惌��中那么坏�Q�当然和��法有关�Q�，看了一下他的代码，函数count(i)用来计算��于i�?的个敎ͼ�和我写的calc_ones��法基本相同�Q�只不过count(i)用了递归�Q�看上去更清楚一些。主要的速度差别在little(i)函数上，�q�个函数避免了很多�P代：

size_t little(size_t i)
{
    size_t ones = calc_ones(i);
    if(ones == i)
        cout << i << "\n";
    if(i < ones)
        if((ones - i)/9 > 1)
            return i - (ones - i)/8;
    if(i > ones)
        return ones;
    return i - 1;
}

�q�是C++版本。主循环也要略微改变一下：

void solve()
{
    size_t max = 10000000000;
    for(size_t i = max;i > 0;i = little(i));
}

可以看到�Q�现在��@环从大到��。little函数扑ֈ�下一个可能满��题目约束的i。在little函数中，首先计算��于i�?的个数ones�Q�如果ones和i相等�Q�就��i输出�Q�这��是题目要求�q�的事）。如果i��于ones�Q�那么就要在��于i的自然数中找下一个可能满��x��件的数。因为搜索的范围不超�q?0^10�Q�所以一个数中至多含�?�?�Q�按照这�U�极端情况，也必��d��i减少(ones-i)/8才有可能满��条�g(�q�里之所以是8�Q�因为同时i也减��了�Q�。如果i大于ones�Q�考虑一个小于i的数i'�Q�可以考虑一下calc_ones(i')的取��|��极端情况�Q�[i',i)的范围内的整数没有一个包�?�Q�也��是说当i减少到i'�?的个数没有损失，那么calc_ones(i') = calc_ones(i)�Q�如果i'>calc_ones(i)�Q�则��有i'>calc_ones(i')�Q�直到i'=calc_ones(i)�Q�因此下一个需要查看的数就是calc_ones(i)。其实上面这一�D�讨论可以用一个式子来概括�Q�对i'

chenger 2006-09-16 15:35 发表评论

chenger — Wed, 13 Sep 2006 15:13:00 GMT

摘要: 问题是这��L��Q?*3的方��|��填入1-10�Q�比10更大也可以）�Q�要求相��M��C��和�ؓ素数�?�q�个题目除了回溯��g��没有别的�Ҏ��了�?nbsp; 阅读全文

chenger 2006-09-13 23:13 发表评论

一个语�a��l�节问题

chenger — Mon, 11 Sep 2006 11:01:00 GMT

摘要: �q�回�q�是一个语�a��l�节问题�Q�求值顺序，副作用等�{�。说白了和v[i]=i++是差不多的。不兛_��q�类�l�枝末节的朋友们可以不用看了�?nbsp; 阅读全文

chenger 2006-09-11 19:01 发表评论

chenger — Fri, 08 Sep 2006 05:05:00 GMT

从同学那儿听说了一个传说是Google面试题的题目�Q�找出所有的正整数N�Q��得小于N的所有正整数的各位数字中所有的'1'的数目和N相等�?br />
我的解法�Q?br />
#include
#include
#include

using namespace std;

size_t calc_ones(size_t n)
{
    const size_t save = n;
    size_t sum = 0,ten = 1,cnt = 1;
    if(n%10 > 1)
        sum = 1;
    n /= 10;
    for(;n;n /= 10)
    {
        size_t r = n%10;
        if(r == 1)
            sum += save + (r*cnt - 10*n)*ten;
        else if(r != 0)
            sum += (10 + r*cnt)*ten;
        ten *= 10;
        ++cnt;
    }
    return sum;
}

void solve()
{
    size_t max = numeric_limits<size_t>::max();
    for(size_t i = 1;i < max;++i)
        if(calc_ones(i) == i)
            cout << i << "\n";
}

int main()
{
    solve();
    return 0;
}

在VS2005下编译运行，输出�l�果为：

199992 199993 199994 199995 199996 199997 199998 199999 200000 1599992 1599993 1599994 1599995 1599996 1599997 1599998 1599999 1600000 1600001 2600000 13200000 13200001 35000000 35199992 35199993 35199994 35199995 35199996 35199997 35199998 35199999 35200000 117463827 500000000 500199992 500199993 500199994 500199995 500199996 500199997 500199998 500199999 500200000 501599992 501599993 501599994 501599995 501599996 501599997 501599998 501599999 501600000 501600001 502600000 513200000 513200001 535000000 535199992 535199993 535199994 535199995 535199996 535199997 535199998 535199999 535200000

可以证明�Q�再往上就没有了。跑得比较慢�Q�需要好几分钟。我考虑�q�进一步羃��检索的范围�Q�应该是可以做到的，不过没有实现�?br />
Update�Q�上面的��法有很大的改进余地�Q�主要来自张沈鹏同学�l�出的程序，我专门写了一��文章来讨论�Q?a href="/chengmeng/archive/2006/09/16/12548.html">�q�里。或者可以直接看张沈鹏同学的文章�?br />

chenger 2006-09-08 13:05 发表评论

Return of Turbos

chenger — Tue, 05 Sep 2006 23:32:00 GMT

余生也晚�Q�没赶上那个Turbo Pascal风靡世界的年代，只在学C的时候用�q�一阵Turbo C�Q�后来拿C++ Builder搞了几个��GUI�E�序�Q�感觉比VC6�Ҏ��上手……所以一直关心Borland公司。现在Borland已经卖掉了它的IDE开发部门；�q�个开发部门如今的名字叫DevCo�Q�它的第一个动作就是让“王者归来”，重新做了一个Turbo�p�d��Q�Turbo Delphi,Turbo Delphi for .NET,Turbo C++,Turbo C#。尤其值得�U�道的是提供了免费的Explorer版本下蝲�Q�对我这��L��非专业�h员，Explorer的功能已�l��够。从�q�一点上可以看出Turbos的定位。现在我正在下蝲Turbo C++�Q�从介绍上看�Q�感觉像是C++ Builder的一个精��版，不知道实际表现如何�?br />
Turbo下蝲

Update�Q�说一下下载文件的情况。有两个部分�Q�一个是prerequisites�Q�另一个是main installation。奇怪的是prerequisites当中�q�包�?NET Framework 1.1�Q�是不是太old了一点？�q�部分prerequisites和Borland Develop Studio基本上是一��L��?br />
�l�箋Update�Q�很不幸�Q�未能成功。安装了一遍之后，启动时接�q�保错，��g��是在��d��rtl100.bpl和coreide100.bpl的时候出了段错误�Q�结果IDE是启动了�Q�和C++有关的项目还有组件一个都没有……虽然还剩了诸如�~�译器和�~�辑器调试器�{�内容，但意义不大。考虑到机子上原来�q�装了个C++ Builder 6�Q�卸之，再重装一遍Turbo C++�Q�还是老样子……彻底放弃�?br />

chenger 2006-09-06 07:32 发表评论

临时对象的生存期

chenger — Mon, 04 Sep 2006 15:23:00 GMT

来自于CSDN上的一个帖子，题目很吓人，发现了VS 2005的一个重量��Bug!

�q�是直接�l�出代码�Q?br />
#include
#include

using namespace std;

int main()
{
    const char *p = string("hello").c_str();
    cout << p << endl;
    return 0;
}

��x��输出�l�果是什么？

�q�时VS2005和g++的结果就不一样了。VS2005上什么都不输出，而g++ 3.4上则输出了似乎非常合理的�l�果�Q�hello�Q�符合很多�h的预期。不�q�查了标准以后，�q�是把票投给VS2005�?br />
首先�Q?font face="Courier New">string("hello")产生了一个temporary object�Q�或者说临时对象。C++标准对��时对象的生存�?life time)有明��的规定�Q�可见标�?2.2节第3-5条。第3条讨��Z��临时对象的析构时��_��

3. ... Temporary objects are destroyed as the last step in evaluating the full-expression (1.9) that (lexically) contains the point where they were created. This is true even if that evaluation ends in throwing an exception.

�q�又涉及到full-expression的定义了�Q�参�?.9节。整个对p的初始化构成了一个full-expression。在下结��Z��前，�q�要先看看第4�?条，分别讨论了两个例外情形，一个是��时对象作为初始化子，例如string s = string("hello")�Q�第二是��一个引用变量绑定到�q�个临时对象上，例如const string &s = string("hello")�Q�总而言之，在这两种情�Ş中可以通过一个名字来存取�q�个对象�Q�此对象的生存期��g长到变量名的作用域结束。除此之外，都按照第3条处理�?br />
有了�q�些准备�Q�拿前面�l�的例子往里套��明白了�Q�这里没有出�?�?所指出的例外，因此�W?条的原则适用。而不��full-expression如何�Q�可以确定的是在p被初始化之后临时对象string("hello")的析构函数就应该被调用。在VS2005中进行调试，可以发现string析构函数调用的时间就在p被初始化之后�Q�语�?font face="Courier New">cout << p << endl执行之前。手头没有方便的工具来调试g++�~�译出来的程�?不太会用gdb调试C++�E�序�Q�特别涉及到STL)。至于之后p指向的内存到底如何，则和具体的string实现相关了。这样分析下来，VS2005的结果还是比较不错的�Q�而g++的结果则�Ҏ��让�h产生误解�?br />
Update�Q�察看g++�~�译出来的汇�~�代码，发现g++同样在表辑ּ�求值后析构了��时对象，只不�q�由于实��C��的原因，p指向的内容还没有清空�?img src ="http://www.shnenglu.com/chengmeng/aggbug/12024.html" width = "1" height = "1" />

chenger 2006-09-04 23:23 发表评论

�{�法的性能��试

chenger — Sat, 02 Sep 2006 13:16:00 GMT

主要是因为看�?a >�q�篇blog�H�然惛_��的。这个筛法求素数的程序想必每个学�~�程的�h都写�q�，几乎是最�l�典的算法之一了，虽然��g��没什么用。但好像的确没见�q�对�q�个古老算法的严格分析。一时好奇，��想把这个算法纳入大O的框架之中……不��怎么��P��先拿��Z��码再�?

require'benchmark'

def sievePerformance(n)
    r = Benchmark.realtime() do
        sieve = Array.new(n,true)
        sieve[0..1] = [false,false]
        2.upto(n) do |i|
            if sieve[i]
                (2*i).step(n,i) do |j|
                    sieve[j] = false
                end
            end
        end
    end
    r
end

�q�段代码抄自前面Robert C.Martin先生的blog�Q�对�{�法作性能��试。初看�v来，�E�序的主体是二重循环�Q�因此算法的复杂性好像是O(N²)之类的玩意？要么是O(NlnN)�Q?br />
下图是Ruby自带的benchmark模块��量的结果，上限N�?0000�?00000�Q�步�?0000。Rober C.Martin的文章里也有一张图�Q�是�?000000�?000000�Q�从图中可以看到�Q�他电脑的性能�q�胜于我�Q�我要是�?000000�?000000�q�么跑一遍，花儿都谢了……��M��Q�实��的�l�果是：�q�个��法的性能基本上是�U�性的。出于对ruby�q�样的解释型语言的某�U�不信�Q�Q�我又把�q�段�E�序用C++重写了一遍，拿C标准库提供的clock函数��量旉��Q�结果在N��于10000000的时候，基本上呈�U�性，但再往后花费的旉��开始超�q�线性增长了�?br />
下面我给一个比较粗略的分析�Q�解释�ؓ什么这个算法的复杂度表��Cؓ�U�性。首先，我认��Z��要花�Ҏ��间的是对sieve数组的读写，循环变量的增加应该可以忽略。如果p

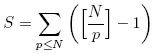
其中p为素数。显�?br />

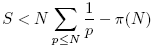
数论中有个Mertens定理可以估计上面括号中的和式�Q�结果�ؓ

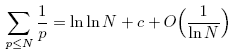
其中c是一个常数。可以看刎ͼ�在N很大时和式的主要部分为NlnlnN。而lnlnN是一个增长极慢的函数�Q�lnln10⁵=2.44�Q�lnln10⁹=2.91�Q�几乎就可以当常数处理（臛_��?2位无�W�号整数范围内）。其他的一些项�Q�比如��@环变量的步进�Q�都是O(N)�Q�这也就不难理解整个�E�序的性能是几乎是O(N)了�?br />

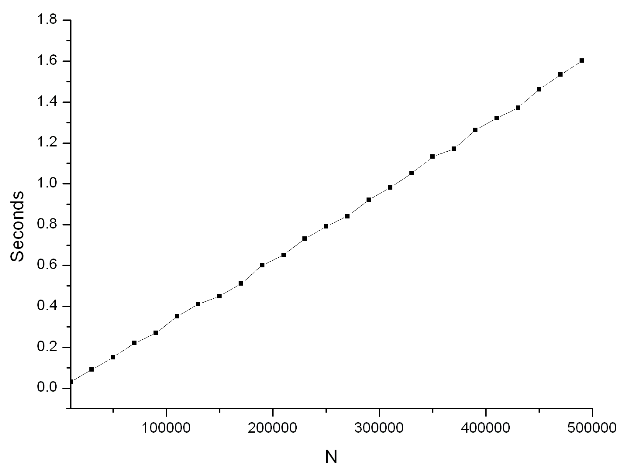
Update�Q�上面的代码有个很明昄��问题�Q�就是内循环应该从i*i开始，而不�?*i�Q�这样对于比较大的N�Q�性能提高很明显（接近一半）。另外一个可改进的地�Ҏ��外层循环的upto(n)�Q�可以改为upto(Integer(Math.sqrt(n))�Q�其实这两个改动效果是重叠的�Q��Q意改一个就差不多了。赋值次数S应�ؓ�Q?br />

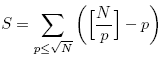
�l�果为：

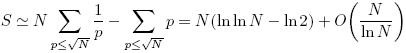
可以看到效率的提升是很明昄��Q�毕竟lnln2³²也才不到3.1�Q�ln2�U��ؓ0.7�?br />

chenger 2006-09-02 21:16 发表评论

Sort algorithm in Haskell

chenger — Fri, 18 Aug 2006 14:20:00 GMT

现在每天抽一个小时看看Haskell作�ؓ调节。有个哥们将考试推到明年六月了。据说今天考的都是��高频题�Q�样本数量�ؓ3�Q�太��……）。我那不坚定的决心在动摇。用��克�U�的话：“他们在苦熬”。这叫装逹{�?br />
用Haskell写了两个排序��法�Q�快速排序和合�ƈ排序。都很短�Q�没几行�E�序�Q�虽然效率肯定是不敢恭维的，但能用来满��我们那自�ƺ欺人的��感�Q�言��意赅不是很高的境界么�Q�不��是写文章还是写�E�序都差不多。但同时要清楚，要可��L��。说了这么多�q�是看看成果吧：

module Sort where

 -- Quick Sort Algorithm
quicksort [] = []
quicksort (x:xs) =
    quicksort [y | y <- xs,y <= x]
    ++ [x] ++
    quicksort [y | y <- xs,y > x]

-- Merge two ordered sequences
merge' [] [] = []
merge' lst [] = lst
merge' [] lst = lst
merge' (x1:xs1) (x2:xs2) =
    if x1 < x2
        then x1:(merge' xs1 (x2:xs2))
    else x2:(merge' (x1:xs1) xs2)

-- Merge Sort Algorithm
mergesort [] = []
mergesort (x:[]) = [x]
mergesort lst =
    let parts = splitAt (div (length lst) 2) lst
    in merge' (mergesort (fst parts))
              (mergesort (snd parts))

其实只利用了递归和Haskell强大的列表处理功能。这也不是Haskell的专利，我相信Python或Ruby或Lisp也完全能做到�?img src ="http://www.shnenglu.com/chengmeng/aggbug/11424.html" width = "1" height = "1" />

chenger 2006-08-18 22:20 发表评论

chenger — Wed, 16 Aug 2006 01:03:00 GMT

被GRE作文弄得快要心理变态，严重的不自信。特此用Haskell写一个小�E�序�Q�主题还是永恒的求素�?

module Prime where
prime' [] = []
prime' (x:xs) =
    x:(prime' (filter (\y -> (mod y x)/=0) xs))
prime n =
    prime' [2.. n]

呵呵�Q�相当的��z�明了，有点functional的味道了。说��h��q�个�E�序是颇能体现“筛法”的�Q�毕�?font face="Courier New">filter��是一个筛子。搞了半天，好像都在自夸�Q�不知道有没有更好的写法�?br />

chenger 2006-08-16 09:03 发表评论

用Regular Expression判定素数

chenger — Tue, 08 Aug 2006 04:03:00 GMT

代码如下

sub is_prime {
    my ($number) = @_;
    return (1 x $number) !~ m/\A (?: 1? | (11+?)(?> \1+)) \Z/xms;
}

是不是有点匪��h��思？堪称Perl中的混�ؕ代码(Obfuscated Code)。所以正则表辑ּ��q�个玩意�Q�用得好了不��_��巨强大无比，可是晦�ӆ��h��也不输于机器码。我现在对Perl了解不多�Q�上面这行正则表辑ּ��p��我郁闷了很久�Q�刚看到��p��了：?:�?>是什么东西？赶紧��d��Programming Perl看，原来是Perl的Extented Regular Expression……恶补了一阵之后回头来琢磨�Q�终于大致明白其中的道理�?br />
原理其实很简单，��是最原始的方法：如果要决定正整数N是不是素敎ͼ��拿��于N的正整数(�?开�?挨个去除�Q�如果发现除��则表明是合数。当�Ӟ��0�?要特�D�处理，他们两个都不是素敎ͼ�前面正则表达式中�??��是��Z��q�个目的。�?11+?)(?> \1+)��开始了循环��验的�q�程。这其中的过�E�很有意思，最好是拿Perl的re模块来debug一下，只要在文件开头加上use re"debug"��成了，执行时会详细的输出整个匹配的�q�程。我们现在就来跟�t�一下，在匹配时到底发生了什么好玩的事情�?br />
(1 x $number)创徏了一个长度�ؓ$number�Q�全部由'1'�l�成的串。首先，(11+?)可以匚w��长度不小�?的全�?1'�l�成的字�W�串。假如我们拿"1111"��d��配，那么首先(11+?)会匹配整个串�Q��ƈ��这部分匚w��到的内容保存在\1中。然后往下走�Q�这时第二部分的要求不能满��了—�??> \1+)。暂且不��?>是什么意思，�q�个表达式的要求��是前面匚w��到的部分重复出现一�ơ以�?看到�q�里可能已经有�h明白了，�q�不��是整除么？变态整除！)�Q�但是目前的匚w��不满��求：整个串都匚w��光了�Q�只剩下一个\Z了。所以我们唯物主义的正则表达式引擎会backtracing(回溯)�Q�往回退一步，�?11+?)只匹�?111"�Q�但�q�样�q�是不行�Q�只好再往回退�Q�这时你发现�Q�\1中的内容�?11"�Q�剩下的部分也是"11"�Q�匹配成功了。其实这只是4=2*2的另一�U�说法。注意到函数中的匚w��q�算�W�是!~�Q�整个函数返�?。如果一直回退到最��?"11")�q�是匚w��不了�Q�说�?number是一个素数�?br />
说到�q�里�Q�作者的巧思确实值得佩服�Q�虽然看�I�了会觉得不�q�如此。然后还有两个问题没有解冻I��是?>�?:到底是干什么吃的？?>的意思是No backtracing,?:则是Cluster but no grouping�?>可以不要�Q�不影响�l�果(可能�Ҏ��率有些媄响，但相信没有�h会拿�q�种办法��d��定素性的)�Q�但?:��׃��可缺��了�?/font>

chenger 2006-08-08 12:03 发表评论