|
|
OpenGL發展的歷史：
OpenGL的前身是SGI公司所開發的IRIS GL圖形函數庫，OpenGL不是一種編程語言，而是一個更像C運行時函數庫。OpenGL是一個開放的工業標準，雖然它是由SGI首創，但它的標準不是控制在SGI手中，而是由OpenGL體系結構審核委員會(ARB)掌管。ARB是由SGC、DEC、IBM、Intel和Microsoft等著名公司于1992年創立，后來陸續加了nVidia、ATI等圖形芯片領域的巨擎。ARB每4年開一次會，對OpenGL規范進行維護和改善，并出臺計劃對OpenGL標準進行升級，使OpenGL一直與時代保持同步。
2006年，SGI公司把OpenGL標準的控制從ARB移交給Khronos小組（www.khronos.org）。Khronos是一個由成員提供資金的行業協會，專注于開放媒體標準的創建和維護。目前Khronos負責OpenGL的發展和升級。
如圖：
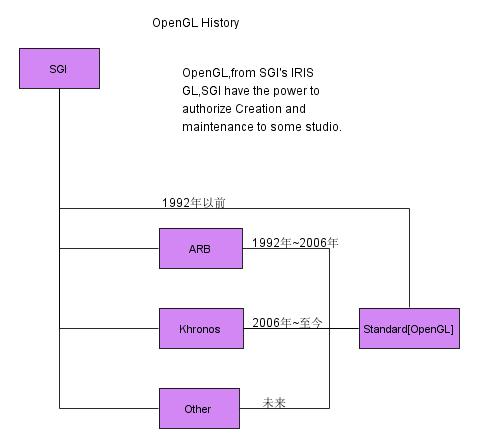
與OpenGL相關的函數庫：
OpenGL工具函數庫(GLU)包含了一些函數，它們利用低層的OpenGL函數來執行一些特定的任務。設定特定的矩陣（gluLookAt等)，OpenGL中的GLU必須以glu開頭。
對于窗口系統的功能也進行了擴展，如果在linux下使用x窗口的話，使用GLX函數庫，而必須以glX開頭。對于微軟來說，以wgl開頭。IBM的os/2而言，PGL是顯示管理器與OpenGL之間的接口，以pgl開頭。對于Apple,AGL是支持OpenGL的系統接口，所有的AGL函數都以agl開頭。
OpenGL實用工具庫( GLUT,OpenGL Utility Toolkit )是Mark Kilgrad所編寫的一個獨立于窗口系統的工具包，它的目的是隱藏不同窗口系統所帶來的復雜性。GLUT是下一節的主題，GLUT函數以glut開頭。
在OpenGL中,我們常用到軌跡球,下面就對軌跡球來做點東西:
當我們觀察三維空間的物體有很多種方法讓一個用戶來選擇一個視點，但是我認為軌跡球是最好的。
軌跡球的基本原理是：
創建一個圍繞著物體的球，然后用戶單擊球上面的一個點，再拖動這個點到一個位置（在屏幕上），讓對象跟著這個向量旋轉。
尋找鼠標位置：
第一步就是尋找到鼠標的位置，我們可以通過獲得視見變換矩陣。
可以通過下面的形式來獲得狀態矩陣：
  GLdouble projection_matrix[16] =  { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 };
GLdouble modelview_matrix[16] = { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 };
int viewport_matrix[4] = { 0, 0, 640, 480 };
glGetDoublev( GL_PROJECTION_MATRIX, projection_matrix );
glGetDoublev( GL_MODELVIEW, modelview_matrix );
glGetIntegerv( GL_VIEWPORT, viewport_matrix );我們獲取這些矩陣后面使用，我們可以使用他們來處理鼠標輸入，鼠標坐標mouse_x和mouse_y，可以通過gluUnProject來獲得鼠標下面場景中的一個點。
GLdouble x, y, z;
gluUnProject( mouse_x, mouse_y,
modelview_matrix,
projection_matrix,
viewport_matrix,
&x, &y, &z );
一旦場景中的這個點被找到，問題的關鍵就是建立一個從攝象機位置到這個點的光線，然后尋找這個光線和這個軌跡球的交點。這個光線是E + t * ( P - E )的點集，這里E是眼睛點位置，P是場景中的那個點，t是一個變量，而軌跡球是S的點集，這里S^2 = r，r是軌跡球的半徑。如果S = E + t * ( P - E )，那么存在一個點既在軌跡球上，又在光線上，這樣，我們可以通過帶入法推出：( E + t * ( P - E ) ) ^ 2 = r。我們知道向量E、P以及標量r，所以可以推出來t，這是一個二次方程，如果無解，說明光線和軌跡球無交點。如果有2個解，應當選擇最靠近眼睛的那個解。
軌跡球的旋轉問題：
如果你單擊拖拽軌跡球上的一個點到另一個位置，該如何做呢？
一個簡單的方法，做起點到結束點的x乘為旋轉軸，然后尋找將要旋轉的角度，這個可以通過做點乘得到。
計算旋轉矩陣：
我們通過四元數來解決它。四元數是二維復數的擴展，特別適合做旋轉。
如果我們有一個單位向量( x, y, z )，我們可以通過乘以旋轉角度的正弦的一半獲得四元數的x, y, z部分的修正值，w是由旋轉角的的余弦的一半決定。大家知道所有的這么值可以被組裝進一個旋轉矩陣：
w * w + x *x - y * y - z * z, 2 * x * y + 2 * w * z, 2 * x * z - 2 * w * y, 0
2 * x * y - 2 * w * z, w * w - x * x + y * y - z * z, 2 * y * z + 2 * w * x, 0
2 * x * z + 2 * w * y, 2 * y * z - 2 * w * x, w * w - x * x - y * y + z * z, 0
0, 0, 0, w * w + x * x + y * y + z * z
|