隨筆檔案

   對(duì)于開(kāi)放列表的維護(hù)方案來(lái)說(shuō)，前面我說(shuō)的，都是一些小花樣了，在一些很小的地圖上用他們并沒(méi)有什么太大的問(wèn)題，但是如果地圖很大，需要搜尋的格子很多，那么開(kāi)放列表里的元素必然會(huì)很多，那么我們是否可以用另外一種思維來(lái)考慮一下開(kāi)放列表的維護(hù)工作？
 
   其實(shí)我們每次從開(kāi)放列表里面取值，每次只需要取里面所有元素的最小值就行了，而前面所說(shuō)的兩種方案都有自己的優(yōu)點(diǎn)，第一種不需要對(duì)開(kāi)放列表做排序，但每次找起最小值來(lái)實(shí)在消耗很大，第2種在找最小值的時(shí)候只需取第一個(gè)元素就行，而麻煩在于需要一直維持開(kāi)放列表里面所有元素的有序排列，那么我們是不是可以把這兩種方法的優(yōu)點(diǎn)都結(jié)合起來(lái)呢

   當(dāng)然，這種方法是有的，那就是很多高級(jí)A*程序更苛求速度的一種做法，利用Binary Heap數(shù)據(jù)結(jié)構(gòu)，也就是二叉堆，來(lái)維護(hù)開(kāi)放列表。

   其實(shí)有關(guān)二叉堆，相信了解他的高手很多，我就不再班門(mén)弄斧，，其實(shí)我也只是剛剛學(xué)習(xí)他而已，這里只簡(jiǎn)單的介紹一下他的一些特點(diǎn)以及在A*中他所起到的作用。

   百度百科中對(duì)二叉堆的定義： 二叉堆是一種特殊的堆，二叉堆是完全二元樹(shù)或者是近似完全二元樹(shù)。二叉堆滿足堆特性：父結(jié)點(diǎn)的鍵值總是大于或等于任何一個(gè)子節(jié)點(diǎn)的鍵值。

   那么應(yīng)用于A*的開(kāi)放列表里，我們只要反過(guò)來(lái)，父結(jié)點(diǎn)的鍵值總是小于或等于任何一個(gè)子節(jié)點(diǎn)的鍵值，這樣就沒(méi)問(wèn)題了。

   利用這種特性進(jìn)行過(guò)排列的開(kāi)放列表，那么我們可以保證，具有F值特性最小的那個(gè)元素，肯定是在這個(gè)二插樹(shù)的根節(jié)點(diǎn)，于是取值的時(shí)候，只要把根節(jié)點(diǎn)上的值取出來(lái)用就行了。（當(dāng)然，取完以后還得維護(hù)開(kāi)放列表的二叉堆特性，這點(diǎn)我下面會(huì)談），一般來(lái)說(shuō)，二叉堆是利用數(shù)組來(lái)表示，那么正好，我所使用的vector結(jié)構(gòu)便可以派上用場(chǎng)，二插堆的結(jié)構(gòu)填往vector中的時(shí)候，利用的是一種類似前序遍歷的方式順序進(jìn)入的，也就是按照 當(dāng)前節(jié)點(diǎn) -- 當(dāng)前節(jié)點(diǎn)的左子節(jié)點(diǎn) -- 當(dāng)前節(jié)點(diǎn)的右子節(jié)點(diǎn)這樣的順序來(lái)放入vector中，如下圖


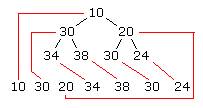
（此圖是借用了Panic所翻譯的《在A*尋路中使用二叉堆》一文中的圖片）

不過(guò)根節(jié)點(diǎn)進(jìn)入的時(shí)候不要放在0號(hào)元素上，vector可以隨便先放進(jìn)一個(gè)沒(méi)有用的元素，我處理的時(shí)候是放了一個(gè)NULL型指針進(jìn)去的，也就是說(shuō)根節(jié)點(diǎn)所在的vector下標(biāo)為1。而這樣的話對(duì)于這個(gè)vector中非0下標(biāo)的任意一個(gè)元素，我們要找他的父節(jié)或者是子節(jié)點(diǎn)就很簡(jiǎn)單了，遵循下面一個(gè)原則：
具備二叉堆特性的vector中下標(biāo)為n(n!=0)的一個(gè)元素：
他的父節(jié)點(diǎn)下標(biāo) = n / 2;(小數(shù)去掉)    比如下標(biāo)為9的元素，他的父節(jié)點(diǎn)下標(biāo)就是4
他的左子節(jié)點(diǎn)下標(biāo) = n * 2;  右子節(jié)點(diǎn)下標(biāo) = n * 2 +1   比如下標(biāo)為3的元素他的左子節(jié)點(diǎn)下標(biāo)為6,右子節(jié)點(diǎn)下標(biāo)為7

   對(duì)于我們的A*來(lái)說(shuō)，在把元素放進(jìn)開(kāi)放列表里面的時(shí)候就需要按照二叉堆的添加步驟進(jìn)行操作，而我們?cè)诎严聵?biāo)1的F值最小的元素取出來(lái)并且刪除掉以后，則需要把二叉堆重新維護(hù)下其二叉堆的特性，而在尋路過(guò)程中某個(gè)開(kāi)放列表中元素的G值改變以后，我們則需要對(duì)這個(gè)開(kāi)放列表再進(jìn)行次維護(hù)，維持他的二叉堆特性。那么綜合以上，我們只需要3個(gè)功能函數(shù)，BinaryHeapAdd函數(shù)，BinaryHeapDelete函數(shù)，RetaxisBinaryHeap函數(shù)

BinaryHeapAdd函數(shù)，
1 把新的要進(jìn)入開(kāi)放列表的元素放進(jìn)vector的末尾，也就是直接push_back進(jìn)去 （這個(gè)新加進(jìn)的元素為當(dāng)前處理元素）
2 利用上面所說(shuō)的父子節(jié)點(diǎn)下標(biāo)關(guān)系，找到當(dāng)前處理元素的父節(jié)點(diǎn)下標(biāo)，然后比較兩個(gè)數(shù)，如果新的元素比他的父節(jié)點(diǎn)小，則把這個(gè)元素和他的父節(jié)點(diǎn)的位置互換一下，如果產(chǎn)生了互換行為，則針對(duì)新位置上的這個(gè)當(dāng)前處理元素再次重復(fù)本次動(dòng)作；
3 直到新的元素大于等于他的父節(jié)點(diǎn)，或者找到的父節(jié)點(diǎn)下標(biāo)為0 ，則新元素的位置確定為找到，這個(gè)函數(shù)可以結(jié)束

void AStarBase::BinaryHeapAdd(POINTINFO* indexPoint)
{
    int tmpF = indexPoint->F;

    _openPoint.push_back(indexPoint);        //先把新的元素放在vector最后

    int theNewIndex = _openPoint.size()-1;   //新元素的下標(biāo)
    while (true)
    {
        int theParentIndex = theNewIndex / 2;     //新元素當(dāng)前所在位置的父節(jié)下標(biāo)
        if (theParentIndex != 0)                  
        {
            if (_openPoint[theNewIndex]->F < _openPoint[theParentIndex]->F)   //新元素的F值比他的父節(jié)點(diǎn)值大
            {
                //與父節(jié)點(diǎn)的位置進(jìn)行交換
                POINTINFO* tmpinfo = _openPoint[theParentIndex];
                _openPoint[theParentIndex] = _openPoint[theNewIndex];
                _openPoint[theNewIndex] = tmpinfo;

                _openPoint[theParentIndex]->openIndex = theParentIndex;
                _openPoint[theNewIndex]->openIndex = theNewIndex;

                theNewIndex = theParentIndex;   //置新節(jié)點(diǎn)的處理下標(biāo)為換過(guò)位置以后的值
            }
            else
            {
                break;
            }
        }
        else                                    //如果父節(jié)下標(biāo)計(jì)算出來(lái)為0，則停止查找位置
        {
            break;
        }
    }
}

BinaryHeapDelete函數(shù)
1 把開(kāi)放列表中1號(hào)元素取出并放在最后返回出來(lái)使用

2 需要對(duì)開(kāi)放列表進(jìn)行一次2叉堆特性重新維護(hù)，首先把vector中最后一個(gè)元素移動(dòng)到1號(hào)下標(biāo)位置，（1號(hào)元素為當(dāng)前處理元素）

3 對(duì)1號(hào)下標(biāo)位置的當(dāng)前處理元素利用父子節(jié)點(diǎn)下標(biāo)計(jì)算關(guān)系找出他的左子節(jié)點(diǎn)和右子節(jié)點(diǎn)，然后把這個(gè)元素與他的左子節(jié)點(diǎn)元素的F值和右子節(jié)點(diǎn)的F值大小分別做比較，如果子節(jié)點(diǎn)的比他更小，則把他與子節(jié)點(diǎn)的位置進(jìn)行互換，如果兩個(gè)子節(jié)點(diǎn)的值都比他小，則與較小的那個(gè)子節(jié)點(diǎn)進(jìn)行位置互換，如果產(chǎn)生了互換行為，則針對(duì)新位置上的當(dāng)前處理元素再次進(jìn)行本次動(dòng)作

4 如果子節(jié)點(diǎn)的值都大于或者等于當(dāng)前處理元素的值，或者計(jì)算出來(lái)的子節(jié)點(diǎn)下標(biāo)已經(jīng)朝出了vector最大元素個(gè)數(shù)，則停止排序，函數(shù)可以返回原來(lái)存起來(lái)的最小值

AStarBase::POINTINFO* AStarBase::BinaryHeapDelete()
{
     if (_openPoint.size() <= 1)   //開(kāi)放列表里面只剩下開(kāi)始放進(jìn)去的一個(gè)空的POINTINFO指針
     {
          return NULL;
     }

     //先把最后一個(gè)元素放到1號(hào)位置
     POINTINFO* tmpinfo = _openPoint[1];    //下標(biāo)1位置的元素先存儲(chǔ)起來(lái)，函數(shù)結(jié)束的時(shí)候要return出去
     _openPoint[1] = _openPoint.back();    //把vector中的最后一個(gè)元素放到下標(biāo)1位置
     _openPoint.pop_back();
     _openPoint[1]->openIndex = 1;

     int theSelectIndex = 1;       //要處理元素的下標(biāo)值
     while (true)
     {
         int theLeftChildIndex = theSelectIndex * 2;               //左子節(jié)點(diǎn)下標(biāo)值
         int theRightChildIndex    = theSelectIndex * 2 + 1;          //右子節(jié)點(diǎn)下標(biāo)值
         if (theLeftChildIndex >= _openPoint.size())   //這個(gè)數(shù)沒(méi)有子節(jié)點(diǎn)，則停止排序
         {
             break;                                   
         }
         else if ( theLeftChildIndex == (_openPoint.size() -1)) //左子節(jié)點(diǎn)正好是vector中最后一個(gè)元素，即只有左子節(jié)點(diǎn)，沒(méi)有右子節(jié)點(diǎn)
         {
             if (_openPoint[theSelectIndex]->F > _openPoint[theLeftChildIndex]->F)   //如果父節(jié)點(diǎn)的F值比左子節(jié)點(diǎn)更大
             {
                 //交換
                 POINTINFO* tmptmpinfo = _openPoint[theLeftChildIndex];
                 _openPoint[theLeftChildIndex] = _openPoint[theSelectIndex];
                 _openPoint[theSelectIndex] = tmptmpinfo;

                 _openPoint[theLeftChildIndex]->openIndex = theLeftChildIndex;
                 _openPoint[theSelectIndex]->openIndex = theSelectIndex;

                 theSelectIndex = theLeftChildIndex;
             }
             else  //如果小，則停止排序
             {
                 break;
             }
         }
         else if (theRightChildIndex < _openPoint.size())  //既有左子節(jié)點(diǎn)又有右子節(jié)點(diǎn)
         {
             if (_openPoint[theLeftChildIndex]->F <= _openPoint[theRightChildIndex]->F )   //左右子節(jié)點(diǎn)先互相比較 左邊的小
             {
                 if (_openPoint[theSelectIndex]->F > _openPoint[theLeftChildIndex]->F)      //處理的父節(jié)點(diǎn)F值比左子節(jié)點(diǎn)大
                 {
                     //交換(與左子節(jié)點(diǎn))
                     POINTINFO* tmptmpinfo = _openPoint[theLeftChildIndex];
                     _openPoint[theLeftChildIndex] = _openPoint[theSelectIndex];
                     _openPoint[theSelectIndex] = tmptmpinfo;     

                     _openPoint[theLeftChildIndex]->openIndex = theLeftChildIndex;
                     _openPoint[theSelectIndex]->openIndex = theSelectIndex;
              
                     theSelectIndex = theLeftChildIndex;
                 }
                 else
                 {
                     break;
                 }
             }
             else     //右邊的比較小
             {
                 if (_openPoint[theSelectIndex]->F > _openPoint[theRightChildIndex]->F)      //處理的F值比右子節(jié)點(diǎn)大
                 {
                     //交換(與右子節(jié)點(diǎn))
                     POINTINFO* tmptmpinfo = _openPoint[theRightChildIndex];
                     _openPoint[theRightChildIndex] = _openPoint[theSelectIndex];
                     _openPoint[theSelectIndex] = tmptmpinfo;

                     _openPoint[theRightChildIndex]->openIndex = theRightChildIndex;
                     _openPoint[theSelectIndex]->openIndex = theSelectIndex;
   
                     theSelectIndex = theRightChildIndex;
                 }
                 else
                 {
                     break;
                 }    
             }
         }

     }
     return tmpinfo;
}

大家可以看到，上面的兩個(gè)函數(shù)所做的添加和刪除操作，可以保證開(kāi)放列表里，1號(hào)位置的元素的F值肯定是最小的，而其他地方的大小位置關(guān)系，我們可以不需要理會(huì)，我們只要保持一個(gè)原則，2叉堆里的父節(jié)點(diǎn)元素F值不能比子節(jié)點(diǎn)大，就可以了

而尋路過(guò)程中由于F值重計(jì)算而導(dǎo)致的重排序，其實(shí)和添加操作的原理是一樣的，我們只需要把那個(gè)改過(guò)F值的元素，把他和他的父節(jié)點(diǎn)的F值進(jìn)行比較，如果改過(guò)的值小，則互換，如果并不小或者沒(méi)有了父節(jié)點(diǎn)，則停止
void AStarBase::RetaxisBinaryHeap(int index)
{
    int theNewIndex = index;   //當(dāng)前處理的下標(biāo)
    while (true)
    {
        int theParentIndex = theNewIndex / 2;     //當(dāng)前處理節(jié)點(diǎn)的父節(jié)點(diǎn)下標(biāo)值
        if (theParentIndex != 0)
        {
            if (_openPoint[theNewIndex]->F < _openPoint[theParentIndex]->F)   //新進(jìn)來(lái)的F值比他的父節(jié)點(diǎn)值大
            {
                //進(jìn)行交換
                POINTINFO* tmpinfo = _openPoint[theParentIndex];
                _openPoint[theParentIndex] = _openPoint[theNewIndex];
                _openPoint[theNewIndex] = tmpinfo;

                _openPoint[theParentIndex]->openIndex = theParentIndex;
                _openPoint[theNewIndex]->openIndex = theNewIndex;

                theNewIndex = theParentIndex;
            }
            else
            {
                break;
            }
        }
        else
        {
            break;
        }
    }
}

利用上面3個(gè)操作函數(shù)所算出來(lái)的尋路結(jié)果，與一開(kāi)始使用在無(wú)序開(kāi)放列表里每次利用比較法找出最小F值所得到的結(jié)果是一樣的，
POINT(2,2)尋路到 POINT(398,398)



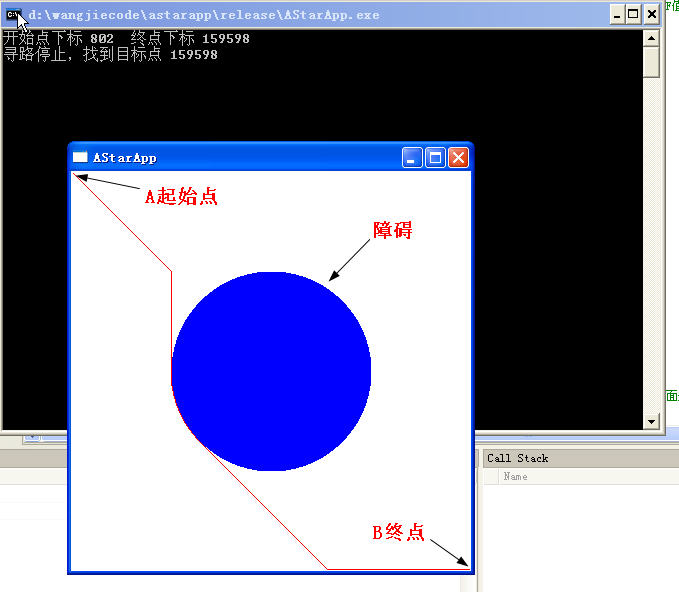
好吧，其實(shí)我們用他的目的是什么？就是要看看他消耗的速度而已，讓我們來(lái)看一下性能分析表


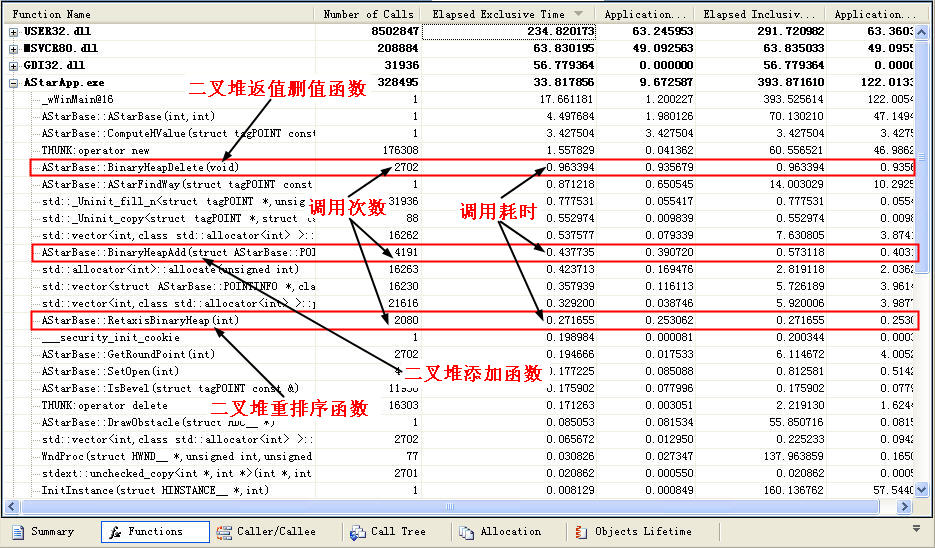
大家可以看到，在整個(gè)程序中這3個(gè)函數(shù)所消耗的時(shí)間為 0.963394 + 0.437735 + 0.271655 = 1.672784毫秒，是無(wú)序找最小值方法所使用時(shí)間的十分之一左右，是使用正常一些全排序方法消耗速度的六分之一左右，這還是在路徑非常簡(jiǎn)單的情況下，而一旦障礙更多，路徑更復(fù)雜，開(kāi)放列表里的元素更多的時(shí)候，Binary Heap方法能體現(xiàn)他更大的速度優(yōu)勢(shì)

以上代碼沒(méi)有經(jīng)過(guò)任何優(yōu)化工作，僅僅是實(shí)現(xiàn)了下二叉堆的功能，各位將就著看了 ^O^

如果對(duì)A*尋路基礎(chǔ)算法原理不清楚并且有興趣的朋友，可以去gameres上看一下這篇文章
http://data.gameres.com/message.asp?TopicID=25439