隨筆檔案

   大家都知道，對(duì)于A*算法，圍繞著開放列表的操作是很多的，開始的時(shí)候需要把當(dāng)前處理點(diǎn)的周圍8個(gè)點(diǎn)里，除了障礙點(diǎn)，已在開放列表里和關(guān)閉列表的點(diǎn)以外的其他點(diǎn)，計(jì)算G,F值以后都放進(jìn)開放列表里，如果已經(jīng)在開啟列表里的，還得對(duì)它進(jìn)行一次G值的重檢測(cè)，從開放列表里每次要找出新的F值最低的點(diǎn)作為當(dāng)前要處理的點(diǎn)，并且要把他從開放列表里面刪除，所以，對(duì)于開放列表的操作的速度，是影響A*尋路速度的第一個(gè)關(guān)卡

   最簡單的一種做法，也是我一開始所使用的方法，剛開始的點(diǎn)按照訪問順序逐一push_back進(jìn)代表開放列表的vector中，（我所用的開放列表用vector來擔(dān)當(dāng)），在取最小值的時(shí)候，使用一個(gè)簡單的算法找出開放列表中具有最小F值的那一個(gè)元素，然后把這個(gè)元素做為當(dāng)前處理的點(diǎn)，并從開放列表里刪除，進(jìn)入關(guān)閉列表，

int AStarBase::FindMinFValue()     //在開放列表中尋找F值最小的(返回的是下標(biāo)值),并且從開放列表里面刪除
{
     if ( _openPoint.empty())
     {
         return -1;
     }
     else
     {
         int id = 0;
         int minIndex = _openPoint[0]->index ;                 
         int theMinF =  _openPoint[0]->F;                      //以第一個(gè)點(diǎn)的F值做為參考值

         for (size_t i = 0;i< _openPoint.size();i++)
         {
             if (theMinF > _openPoint[i]->F)                 //如果找到比他更小的F值,則把新的F值做為當(dāng)前參考值
             {
                  id = i;
                  minIndex = _openPoint[i]->index;
                  theMinF = _openPoint[i]->F;
             }
         }
         _openPoint.erase(_openPoint.begin() + id);        //刪除所找到的元素

         return minIndex;                                
     }
}

   這真的是最容易實(shí)現(xiàn)的方法了，他唯一的一點(diǎn)好處是由于開放列表里的所有元素一直都是無序的狀態(tài)，所以在后期出現(xiàn)開放列表里某個(gè)元素的G值被改變的時(shí)候，開放列表不需要重新排序，但是他的執(zhí)行速度呢？大家可以看一下我的第一篇A*隨筆里所貼的圖片，從POINT(2,2)點(diǎn)尋路到POINT(398,398)的位置，下標(biāo)元素從802開始尋找到159598，這么多個(gè)點(diǎn)，消耗在開放列表尋值的時(shí)間是多少呢？
  
   正好，我們的Visual studio給我們提供了一個(gè)程序性能分析工具，可以具體的分析出程序中每一個(gè)函數(shù)的調(diào)用情況，我們可以用他大概的查看一下我們的這個(gè)函數(shù)的執(zhí)行情況


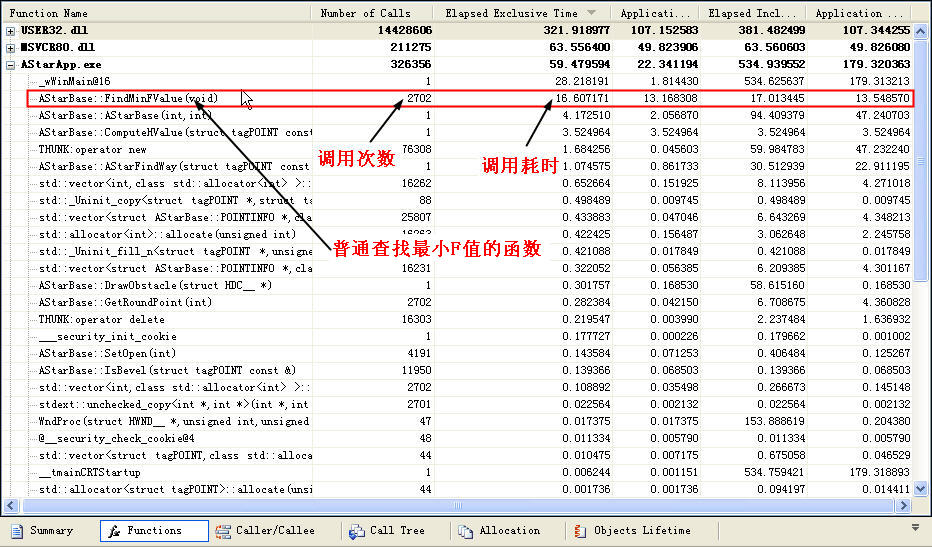
上圖中的可看出，整個(gè)尋路過程中，花費(fèi)在每次找出最小值FindMinFValue()這個(gè)函數(shù)的總時(shí)間為16.60毫秒。恩，這個(gè)貌似是很快的么，不是么，才16.6豪秒而已，人類根本是察覺不出這樣的時(shí)間花費(fèi)的，OK,那讓我們接著往下看吧

恩，如果不想每次都花費(fèi)死工夫在無序的開放列表里面找F最小的元素，那么我們一開始在往里面放東西的時(shí)候，就讓他們排好序不就行了嗎？從小到大排序，那么每次具有最小F值的那個(gè)元素肯定在首位了，每次取他就行了。 恩，其實(shí)有現(xiàn)成的自動(dòng)排序的STL容器可以用，但我不想用他，用自己的排序方法去維護(hù)開放列表好了。

對(duì)于排序算法，網(wǎng)上現(xiàn)成的算法有很多了，什么選擇啊，冒泡啊，快速啊，恩，我自己稍微寫了一下，用的還是一種比較死的方法，就是每次在往開放列表里放新元素的時(shí)候，找好了位置再放，保證放過以后開放列表里面的所有元素都是按F從小到大進(jìn)行排列的。
void AStarBase::InsertToOpenList(POINTINFO* indexPoint)    //利用插入法往開放列表里放點(diǎn)(F值從小到大)
{
     int tmpF = indexPoint->F;
   
     if (_openPoint.empty())
     {
         _openPoint.push_back(indexPoint);
         return;
     }
     for (AStarBase::PixelContain::iterator it = _openPoint.begin();it != _openPoint.end();it++)
     {
         if ( (*it)->F >= tmpF)   //找到比F值大的了，就插在他的前面
         {
             _openPoint.insert(it,indexPoint);
             return;
         }
     }

     _openPoint.push_back(indexPoint);  
}

其實(shí)比他快的方法還有很多，比如先push_back，再利用快速排序?qū)φ麄€(gè)開放列表進(jìn)行排序,但這里我這里也就簡單的寫寫了，好吧，我們看下這種方法的結(jié)果，不過很可惜，僅僅這么做得到的是錯(cuò)誤的結(jié)果，


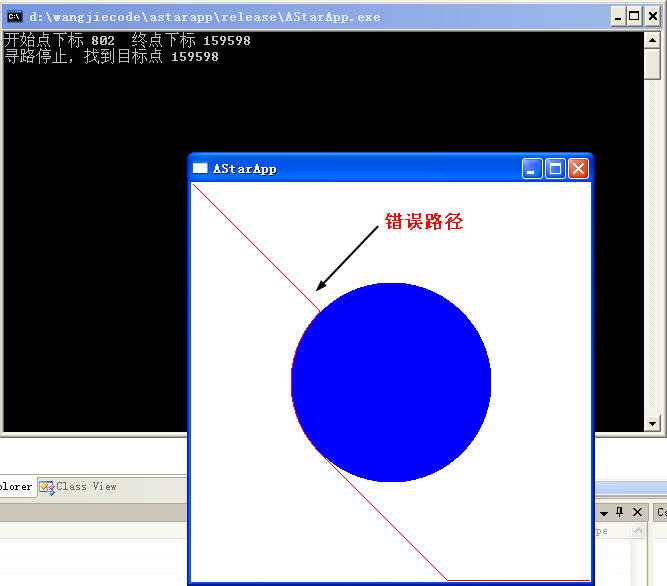
   為什么說他是錯(cuò)誤的呢，因?yàn)樵趯ぢ愤^程中少做了一步針對(duì)開放列表的重排序，因?yàn)樵谟幸粋€(gè)步驟中，開放列表里的有些點(diǎn)的G值會(huì)經(jīng)過重新計(jì)算可以得到一個(gè)更小的G值，而F值也會(huì)更小，所以這時(shí)候需要對(duì)開放列表做下重排序，重排序其實(shí)也很簡單，只要找到這個(gè)改過g值的元素在開放列表里的位置，然后把他和處于他前面的元素進(jìn)行下比較，把他重新放在一個(gè)合適他的位置就可以保持開放列表的有序了，這一步我就沒有做了，我僅僅想看一下這個(gè)每次插入排序所用的時(shí)間消耗
  

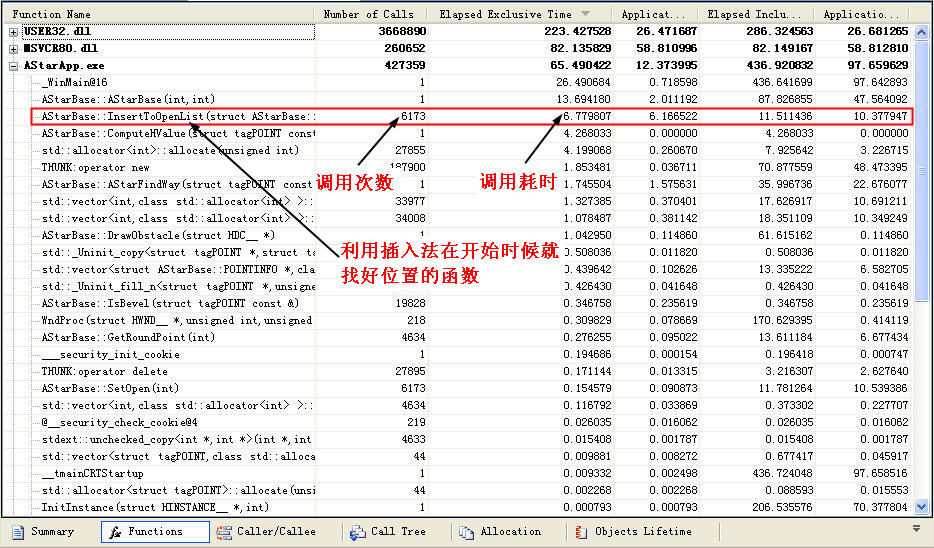
大家可以看到，這個(gè)函數(shù)總共耗時(shí)在6.7毫秒，而這個(gè)程序中并沒有處理F值改變時(shí)候的開放列表重排序問題，不過我估計(jì)，如果把這個(gè)處理函數(shù)加進(jìn)去，他的消耗也不會(huì)比上面這個(gè)函數(shù)所用的時(shí)間更多，估計(jì)大概在不到5毫秒左右的時(shí)間，也就是說，針對(duì)開放列表進(jìn)行排序維護(hù)的話，總時(shí)間消耗大概在12毫秒左右，如果使用一些小的技巧，一些好的常用排序算法針對(duì)排序進(jìn)行優(yōu)化的話，這個(gè)時(shí)間還能縮短到10毫秒以內(nèi),很不錯(cuò)的不是嗎？在維護(hù)開放列哦上的效率能提高的接近50%呢。

（呵呵，這里有些偷懶，并沒有針對(duì)常用的排序方法把這里做完，只是弄了一個(gè)錯(cuò)誤的東西上來估計(jì)了一下，大家莫怪，其實(shí)這些肯定是大家早已經(jīng)研究過很多次的地方了，而我想談?wù)摰闹攸c(diǎn)，也并不在于此）


以上只是一個(gè)A*初學(xué)者對(duì)于A*的一些想法，還請(qǐng)高手多多指正
如果對(duì)A*尋路基礎(chǔ)算法原理不清楚并且有興趣的朋友，可以去gameres上看一下這篇文章
http://data.gameres.com/message.asp?TopicID=25439