今天08、09的個人排位賽,出了下面這道,一開始看覺得很難,后來推出來了后就不是很難了。
哈哈,只有我一個人做出來,下面說下怎么做。
題目定義一種叫做n-circle five-angle 的圖,問生成樹的個數(shù),每個點(diǎn)都算一個不同的點(diǎn)
Illustration 1: 4-circle five-angle graph
首先,中間的環(huán)肯定要去掉一些,但是去掉多少條、哪幾條呢?
可以枚舉情況。就拿樣例說,我們?nèi)サ羧我獾膬蓷l,得到下圖:
紅色的邊表示去掉的。
1)對于非紅色邊組成的環(huán),4條邊任意一條都能刪除,即4n-i 這里i是中間環(huán)要刪除的邊數(shù)
2)對于紅色邊組成的環(huán),這4*i條邊只能刪除一條,刪多了就會不連通了,也即4*i種
再乘上一個組合數(shù)C(n,i)即可
所以F(n) = ∑ 4n-i*4*i*C(n,i) 1≤i≤n
樣例給了2,注意是2條平行邊形成的環(huán)!
 #include<cstdio>
#include<cstdio>
 #include<cstring>
#include<cstring>

 int C[101][101],F[101];
int C[101][101],F[101];

 int pow4(int n)//4^n
int pow4(int n)//4^n


 {
{
 int ans=1,p=4;
int ans=1,p=4;
 while(n)
while(n)


 {
{
 if(n&1)ans=ans*p%2007;
if(n&1)ans=ans*p%2007;
 p=p*p%2007;
p=p*p%2007;
 n>>=1;
n>>=1;
 }
}
 return ans;
return ans;
 }
}
 int main()
int main()


 {
{
 //freopen("in","r",stdin);
//freopen("in","r",stdin);
 //freopen("out","w",stdout);
//freopen("out","w",stdout);
 for(int i=1;i<=100;i++)
for(int i=1;i<=100;i++)


 {
{
 C[i][i]=C[i][0]=1;
C[i][i]=C[i][0]=1;
 for(int j=1;j<i;j++)
for(int j=1;j<i;j++)
 C[i][j]=(C[i-1][j]+C[i-1][j-1])%2007;
C[i][j]=(C[i-1][j]+C[i-1][j-1])%2007;
 }
}
 for(int n=2;n<=100;n++)
for(int n=2;n<=100;n++)


 {
{
 F[n]=0;
F[n]=0;
 for(int i=1;i<=n;i++)
for(int i=1;i<=n;i++)
 F[n]=(F[n]+pow4(n-i)*4*i*C[n][i])%2007;
F[n]=(F[n]+pow4(n-i)*4*i*C[n][i])%2007;
 }
}
 int n,T;
int n,T;
 scanf("%d",&T);
scanf("%d",&T);
 while(T--)
while(T--)


 {
{
 scanf("%d",&n);
scanf("%d",&n);
 printf("%d\n",F[n]);
printf("%d\n",F[n]);
 }
}
 return 0;
return 0;
 }
}附題目:
Problem A. Spanning Tree
A peculiar graph, called n-circle five-angle graph, consists of a polygon with n vertices in the center, and each side of the central polygon is linked with a pentagon(pentagon: a polygon with 5 sides). There is an example of 4-circle five-angle graph below. Obviously, there are 4 vertices in the central polygon.
Now, it is you time to calculate how many spanning trees could this special graph generate. Pay attention that all the vertices in the graph should be regarded as different ones. Do you still remember the definition of spanning tree? Perhaps you may be familiar with the terminology of MST(minimal spanning tree). Yes, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some (or perhaps all) of the edges of G.
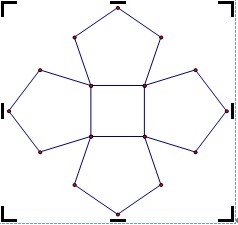
Illustration 1: 4-circle five-angle graph
Input:
First line: T, the number of test case.
Then follow T lines, each line contains a number n(n <= 2 <= 100), indicating it is an n-circle five-angle graph.
Output:
For each test case, output the answer mod 2007 pre line.
Sample Input
Sample Output
測試數(shù)據(jù):in.txt out.txt