   /**//* /**//*
 N行,有M個僵尸,有K個堅果,按順序從給定線路水平滾出 N行,有M個僵尸,有K個堅果,按順序從給定線路水平滾出
 堅果撞到僵尸或者邊界都會改變路線以45°滾動,問最后多少只僵尸被撞到了 堅果撞到僵尸或者邊界都會改變路線以45°滾動,問最后多少只僵尸被撞到了
 N<=2000, M<=200000, K<=100000 N<=2000, M<=200000, K<=100000

 我之前是按順序模擬堅果滾動,超時了 我之前是按順序模擬堅果滾動,超時了
 雖然我也是建了list之類的,我知道的是能用x+y,x-y的值來表示直線 雖然我也是建了list之類的,我知道的是能用x+y,x-y的值來表示直線
 復雜度應該是O(MlogM + K) 復雜度應該是O(MlogM + K)

 watashi解題報告說可以用鏈表類似Dancing Links啥的搞到O(M+K),但是編程量巨大 watashi解題報告說可以用鏈表類似Dancing Links啥的搞到O(M+K),但是編程量巨大
 他自己的做法很神奇!!!! 他自己的做法很神奇!!!!
 反過來做,對僵尸按X排序,從左到右,檢查該僵尸會被哪只堅果撞到(其實就是被編號最小的撞到) 反過來做,對僵尸按X排序,從左到右,檢查該僵尸會被哪只堅果撞到(其實就是被編號最小的撞到)
 一只僵尸(x,y)可以被3個方向撞到(y=1,n時兩個),路線的方程就是 一只僵尸(x,y)可以被3個方向撞到(y=1,n時兩個),路線的方程就是
 x - y = k1 , x + y = k2 , y = k3 x - y = k1 , x + y = k2 , y = k3
 因此需要找到滿足上面方程之一的堅果,而且編號最小的 因此需要找到滿足上面方程之一的堅果,而且編號最小的
 直接這樣搞,方程很多的,我之前就是這樣子搞 直接這樣搞,方程很多的,我之前就是這樣子搞 .. ..

 注意到x-y = k1與x-2(n-1)-y=k1是同一條路線的,所以可以對(x-y)%2(n-1),x+y也一樣 注意到x-y = k1與x-2(n-1)-y=k1是同一條路線的,所以可以對(x-y)%2(n-1),x+y也一樣
 取模了后本來x-y很大的,就變為很小了,而且是可唯一標示出來的 取模了后本來x-y很大的,就變為很小了,而且是可唯一標示出來的

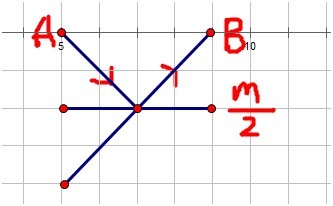
 兩個點A,B若在同一條路線上,若他們都向下或向上的話,顯然 兩個點A,B若在同一條路線上,若他們都向下或向上的話,顯然
 y1-x1 = y2-x2 mod m , m-(y1+x1) = m-(y2+x2) mod m y1-x1 = y2-x2 mod m , m-(y1+x1) = m-(y2+x2) mod m
 若一上一下,就 y1-x1 = m-(y2+x2) mod m 若一上一下,就 y1-x1 = m-(y2+x2) mod m
 這樣一條路線就能用一個值來表示了,即在點(x,y)處, 這樣一條路線就能用一個值來表示了,即在點(x,y)處,
 ---------------------------------------------- ----------------------------------------------
 |若向下則該路線的值(y-x) mod m | |若向下則該路線的值(y-x) mod m |
 |若向上則該路線的值m-(y+x) mod m | |若向上則該路線的值m-(y+x) mod m |
 ---------------------------------------------- ----------------------------------------------
 為什么能這樣表示呢? 為什么能這樣表示呢?
 比如向下的直線方程為y-x = k1,向上的為y+x=k2 比如向下的直線方程為y-x = k1,向上的為y+x=k2
 他們關于邊界對稱,則有k1+k2 = m,即k1 = m - k2,所以用K1,m-k2就能唯一表示線路了(曲折的,不是直線) 他們關于邊界對稱,則有k1+k2 = m,即k1 = m - k2,所以用K1,m-k2就能唯一表示線路了(曲折的,不是直線)
 \ / \ /
 \/ \/
 ------- m/2 下面的那個是引出的,上面的是實際路線,顯然這兩條直線跟y軸的交點之和k1+k2為m ------- m/2 下面的那個是引出的,上面的是實際路線,顯然這兩條直線跟y軸的交點之和k1+k2為m
 / /
 / /

 在起始處總共也就只會有n-1條向下的,n-1條向上的,n條水平的,這2*(n-1)+n條直線就會鋪滿整個地圖了 在起始處總共也就只會有n-1條向下的,n-1條向上的,n條水平的,這2*(n-1)+n條直線就會鋪滿整個地圖了
 因此可編碼為 [0,n-1)的為向下的,[n-1,2(n-1))向上的,[2*(n-1),3*n-2)水平的 因此可編碼為 [0,n-1)的為向下的,[n-1,2(n-1))向上的,[2*(n-1),3*n-2)水平的

 啟示:處理好同一條路線怎么用一個值來表示 啟示:處理好同一條路線怎么用一個值來表示

 枚舉點(x,y)可能被幾個方向撞到的線路,這些路線就是m+y, (y-x) mod m , m-(y+x) mod m 枚舉點(x,y)可能被幾個方向撞到的線路,這些路線就是m+y, (y-x) mod m , m-(y+x) mod m
 最后就用優先隊列來搞,取編號最小的路線,因為最先被這個撞到了~~~ 最后就用優先隊列來搞,取編號最小的路線,因為最先被這個撞到了~~~
 處理好一列后,注意加入新的堅果路線(因為撞了后改變路線了) 處理好一列后,注意加入新的堅果路線(因為撞了后改變路線了)

 神奇丫神奇丫~~~~ 神奇丫神奇丫~~~~


 以上只是我膜拜了watashi的代碼后的一點想法而已,建議直接看他的代碼~~~ 以上只是我膜拜了watashi的代碼后的一點想法而已,建議直接看他的代碼~~~
 */ */
 #include<iostream> #include<iostream>
 #include<cstring> #include<cstring>
 #include<map> #include<map>
 #include<algorithm> #include<algorithm>
 #include<stack> #include<stack>
 #include<queue> #include<queue>
 #include<cmath> #include<cmath>
 #include<string> #include<string>
 #include<cstdlib> #include<cstdlib>
 #include<vector> #include<vector>
 #include<cstdio> #include<cstdio>
 #include<set> #include<set>
 #include<list> #include<list>
 #include<numeric> #include<numeric>
 #include<cassert> #include<cassert>
 #include<ctime> #include<ctime>
 #include<bitset> #include<bitset>

 using namespace std; using namespace std;

 const int MAXN =200000; const int MAXN =200000;

 pair<int,int> pt[MAXN]; pair<int,int> pt[MAXN];
 priority_queue<int, vector<int>, greater<int> > pq[6000];//最小堆 priority_queue<int, vector<int>, greater<int> > pq[6000];//最小堆

  inline int mod(int a, int b) inline int mod(int a, int b)  { {
 a %= b; a %= b;
 return a < 0 ? a + b : a; return a < 0 ? a + b : a;
 } }

 int main() int main()
   { {
 #ifndef ONLINE_JUDGE #ifndef ONLINE_JUDGE
 freopen("in","r",stdin); freopen("in","r",stdin);
 #endif #endif

 int T, N, M, K; int T, N, M, K;
  for(scanf("%d", &T); T--; ) for(scanf("%d", &T); T--; )  { {
 scanf("%d%d%d", &N, &M, &K); scanf("%d%d%d", &N, &M, &K);
 int m = 2*(N-1); int m = 2*(N-1);

  for(int k = 0; k < m + N ; k++) for(int k = 0; k < m + N ; k++)  { {
  while(!pq[k].empty()) while(!pq[k].empty()) { {
 pq[k].pop(); pq[k].pop();
 } }
 } }

  for (int i = 0; i < M; i ++) for (int i = 0; i < M; i ++)  { {
 scanf("%d%d", &pt[i].first, &pt[i].second); scanf("%d%d", &pt[i].first, &pt[i].second);
 pt[i].second --; pt[i].second --;
 } }
 sort(pt, pt+M); sort(pt, pt+M);

  for (int i = 0, t; i < K; i ++) for (int i = 0, t; i < K; i ++)  { {
 scanf("%d", &t); scanf("%d", &t);
 pq[m+t-1].push(i); pq[m+t-1].push(i);
 } }

 int lastx = 0, ans = 0; int lastx = 0, ans = 0;
 vector<pair<int,int> > r; vector<pair<int,int> > r;
  for(int i = 0; i < M; i ++) for(int i = 0; i < M; i ++)  { {
 int x = pt[i].first , y = pt[i].second; int x = pt[i].first , y = pt[i].second;
  if (x > lastx) if (x > lastx)  {//處理完一列后注意加入新的堅果路線 {//處理完一列后注意加入新的堅果路線
 lastx = x; lastx = x;
  for (vector<pair<int,int> >::iterator it = r.begin() ; it != r.end(); it ++) for (vector<pair<int,int> >::iterator it = r.begin() ; it != r.end(); it ++)  { {
 pq[it->first].push(it->second); pq[it->first].push(it->second);
 } }
 r.clear(); r.clear();
 } }

 int j = -1, t; int j = -1, t;
  if(!pq[t = m+y].empty() && (j == -1 || pq[t].top() < pq[j].top())) if(!pq[t = m+y].empty() && (j == -1 || pq[t].top() < pq[j].top())) {// horizonal {// horizonal
 j = t; j = t;
 } }
  if(!pq[t = mod(y-x, m)].empty() && ( j == -1 || pq[t].top() < pq[j].top()) ) if(!pq[t = mod(y-x, m)].empty() && ( j == -1 || pq[t].top() < pq[j].top()) ) { //buttom right { //buttom right
 j = t; j = t;
 } }
  if(!pq[t = mod(m-(y+x), m)].empty() && ( j == -1 || pq[t].top() < pq[j].top()) ) if(!pq[t = mod(m-(y+x), m)].empty() && ( j == -1 || pq[t].top() < pq[j].top()) ) { //top right { //top right
 j = t; j = t;
 } }

  if(j == -1) if(j == -1) { {
 continue; continue;
 } }

 ans ++; ans ++;
 t = pq[j].top(); t = pq[j].top();
 pq[j].pop(); pq[j].pop();
  if(j < m) if(j < m) { {
 r.push_back(make_pair(mod(m-j-2*x, m),t)); r.push_back(make_pair(mod(m-j-2*x, m),t));
  }else }else  { {
 j -= m; j -= m;
  if(j < N/2) if(j < N/2)  {//buttom right {//buttom right
 r.push_back(make_pair(mod(y-x,m),t)); r.push_back(make_pair(mod(y-x,m),t));
  } else } else  {//top right {//top right
 r.push_back(make_pair(mod(m-(y+x),m),t)); r.push_back(make_pair(mod(m-(y+x),m),t));
 } }
 } }
 } }
 printf("%d\n" , ans); printf("%d\n" , ans);
 } }
 return 0; return 0;
 } }

|
|
常用鏈接
隨筆分類
Links
搜索
最新評論

|
|