原諒轉(zhuǎn)載自:
http://www.cnblogs.com/skywang12345/p/3245399.html
紅黑樹(一) 原理和算法詳細(xì)介紹
作者:Sky Wang 于 2013-08-08
概述:R-B Tree,又稱為“紅黑樹”。本文參考了《算法導(dǎo)論》中紅黑樹相關(guān)知識(shí),加之自己的理解,然后以圖文的形式對(duì)紅黑樹進(jìn)行說明。本文的主要內(nèi)容包括:紅黑樹的特性,紅黑樹的時(shí)間復(fù)雜度和它的證明,紅黑樹的左旋、右旋、插入、刪除等操作。
請(qǐng)尊重版權(quán),轉(zhuǎn)載注明出處:http://www.cnblogs.com/skywang12345/p/3245399.html
1 R-B Tree簡介
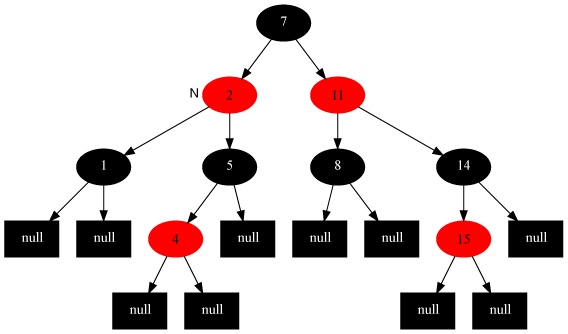
R-B Tree,全稱是Red-Black Tree,又稱為“紅黑樹”,它一種特殊的二叉查找樹。紅黑樹的每個(gè)節(jié)點(diǎn)上都有存儲(chǔ)位表示節(jié)點(diǎn)的顏色,可以是紅(Red)或黑(Black)。
紅黑樹的特性:
(1)每個(gè)節(jié)點(diǎn)或者是黑色,或者是紅色。
(2)根節(jié)點(diǎn)是黑色。
(3)每個(gè)葉子節(jié)點(diǎn)(NIL)是黑色。 [注意:這里葉子節(jié)點(diǎn),是指為空(NIL或NULL)的葉子節(jié)點(diǎn)!]
(4)如果一個(gè)節(jié)點(diǎn)是紅色的,則它的子節(jié)點(diǎn)必須是黑色的。
(5)從一個(gè)節(jié)點(diǎn)到該節(jié)點(diǎn)的子孫節(jié)點(diǎn)的所有路徑上包含相同數(shù)目的黑節(jié)點(diǎn)。
注意:
(01) 特性(3)中的葉子節(jié)點(diǎn),是只為空(NIL或null)的節(jié)點(diǎn)。
(02) 特性(5),確保沒有一條路徑會(huì)比其他路徑長出倆倍。因而,紅黑樹是相對(duì)是接近平衡的二叉樹。
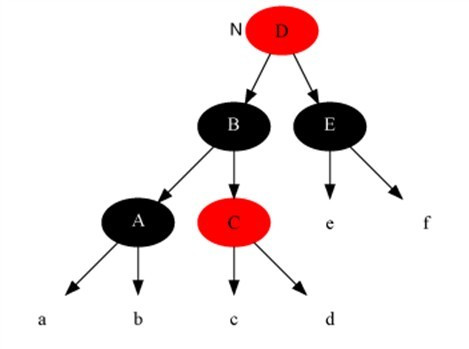
紅黑樹示意圖如下:
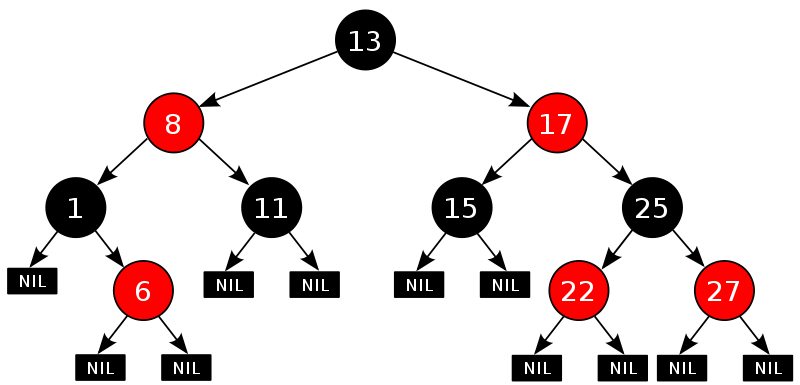
紅黑樹的應(yīng)用:
紅黑樹的應(yīng)用比較廣泛,主要是用它來存儲(chǔ)有序的數(shù)據(jù),它的時(shí)間復(fù)雜度是O(lgn),效率非常之高。
例如,Java中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虛擬內(nèi)存的管理,都是通過紅黑樹去實(shí)現(xiàn)的。
這里大致介紹下,紅黑樹和AVL樹的差異。AVL樹也是特殊的二叉樹,它的特性是“任何節(jié)點(diǎn)的左右子樹的高度之差不超過1”。基本上,用到紅黑樹的地方都可以用AVL樹(自平衡二叉查找樹)去替換。但是一般情況下,在執(zhí)行添加、刪除節(jié)點(diǎn)時(shí),AVL樹比紅黑樹執(zhí)行的操作更多一些,效率更低一些;而且紅黑樹也是相對(duì)平衡的二叉樹(從一個(gè)節(jié)點(diǎn)到該節(jié)點(diǎn)的子孫節(jié)點(diǎn)的所有路徑上包含相同數(shù)目的黑節(jié)點(diǎn))。因此,紅黑樹的效率會(huì)高更一點(diǎn)。
2 R-B Tree時(shí)間復(fù)雜度
紅黑樹的時(shí)間復(fù)雜度為: O(lgn)
下面通過“數(shù)學(xué)歸納法”對(duì)紅黑樹的時(shí)間復(fù)雜度進(jìn)行證明。
定理:一棵含有n個(gè)節(jié)點(diǎn)的紅黑樹的高度至多為2log(n+1).
證明:
"一棵含有n個(gè)節(jié)點(diǎn)的紅黑樹的高度至多為2log(n+1)" 的逆否命題是 "高度為h的紅黑樹,它的包含的內(nèi)節(jié)點(diǎn)個(gè)數(shù)至少為 2^{h/2}-1個(gè)"。
我們只需要證明逆否命題,即可證明原命題為真;即只需證明 "高度為h的紅黑樹,它的包含的內(nèi)節(jié)點(diǎn)個(gè)數(shù)至少為 2^{h/2}-1個(gè)"。
從某個(gè)節(jié)點(diǎn)x出發(fā)(不包括該節(jié)點(diǎn))到達(dá)一個(gè)葉節(jié)點(diǎn)的任意一條路徑上,黑色節(jié)點(diǎn)的個(gè)數(shù)稱為該節(jié)點(diǎn)的黑高度,記為bh(x)。
由紅黑樹的"特性(4)"可知 bh(x)>=h/2;進(jìn)而,我們只需證明 "高度為h的紅黑樹,它的包含的內(nèi)節(jié)點(diǎn)個(gè)數(shù)至少為 2^bh(x)-1個(gè)"即可。
到這里,我們將需要證明的定理已經(jīng)由
"一棵含有n個(gè)節(jié)點(diǎn)的紅黑樹的高度至多為2log(n+1)"
轉(zhuǎn)變成只需要證明
"高度為h的紅黑樹,它的包含的內(nèi)節(jié)點(diǎn)個(gè)數(shù)至少為 2^bh(x)-1個(gè)"。
下面通過"數(shù)學(xué)歸納法"開始論證高度為h的紅黑樹,它的包含的內(nèi)節(jié)點(diǎn)個(gè)數(shù)至少為 2^bh(x)-1個(gè)"。
(01) 當(dāng)樹的高度h=0時(shí),
內(nèi)節(jié)點(diǎn)個(gè)數(shù)是0,bh(x) 為0,2^bh(x)-1 也為 0。顯然,原命題成立。
(02) 當(dāng)h>0,且樹的高度為 h-1 時(shí),它包含的節(jié)點(diǎn)個(gè)數(shù)至少為 2^{bh(x)-1}-1。這個(gè)是根據(jù)(01)推斷出來的!
下面,由樹的高度為 h-1 的已知條件推出“樹的高度為 h 時(shí),它所包含的節(jié)點(diǎn)樹為 2^bh(x)-1”。
當(dāng)樹的高度為 h 時(shí),
對(duì)于節(jié)點(diǎn)x(x為根節(jié)點(diǎn)),其黑高度為bh(x)。
對(duì)于節(jié)點(diǎn)x的左右子樹,它們黑高度為 bh(x) 或者 bh(x)-1。
根據(jù)(02)的已知條件,我們已知 "x的左右子樹,即高度為 h-1 的節(jié)點(diǎn),它包含的節(jié)點(diǎn)至少為 2^{bh(x)-1}-1 個(gè)";
所以,節(jié)點(diǎn)x所包含的節(jié)點(diǎn)至少為 ( 2^{bh(x)-1}-1 ) + ( 2^{bh(x)-1}-1 ) + 1 = 2^{bh(x)-1}。即節(jié)點(diǎn)x所包含的節(jié)點(diǎn)至少為 2^{bh(x)-1} 。
因此,原命題成立。
由(01)、(02)得出,"高度為h的紅黑樹,它的包含的內(nèi)節(jié)點(diǎn)個(gè)數(shù)至少為 2^bh(x)-1個(gè)"。
因此,“一棵含有n個(gè)節(jié)點(diǎn)的紅黑樹的高度至多為2log(n+1)”。
3 R-B Tree基本操作
R-B Tree的基本操作是添加、刪除。
添加和刪除操作,都會(huì)用到兩個(gè)基本的方法:左旋 和 右旋,統(tǒng)稱為旋轉(zhuǎn)。旋轉(zhuǎn)是為了保持紅黑樹的特性而提供的輔助方法,因?yàn)楫?dāng)我們進(jìn)行添加、刪除節(jié)點(diǎn)時(shí),可能改變紅黑樹的特性(例如,刪除一個(gè)黑色節(jié)點(diǎn)之后,就不滿足“從一個(gè)節(jié)點(diǎn)到該節(jié)點(diǎn)的子孫節(jié)點(diǎn)的所有路徑上包含相同數(shù)目的黑節(jié)點(diǎn)”這個(gè)特性);這里,我們就需要旋轉(zhuǎn)方法的輔助來讓樹保持紅黑樹的特性。
3.1 左旋

上面是《算法導(dǎo)論》中左旋的示意圖。
參考上面的示意圖和下面的偽代碼,理解“紅黑樹T的節(jié)點(diǎn)x進(jìn)行左旋”是如何進(jìn)行的。
LEFT-ROTATE(T, x)
01 y ← right[x] // 前提:這里假設(shè)x的右孩子為y。下面開始正式操作
02 right[x] ← left[y] // 將 “y的左孩子” 設(shè)為 “x的右孩子”,即 將β設(shè)為x的右孩子
03 p[left[y]] ← x // 將 “x” 設(shè)為 “y的左孩子的父親”,即 將β的父親設(shè)為x
04 p[y] ← p[x] // 將 “x的父親” 設(shè)為 “y的父親”
05 if p[x] = nil[T]
06 then root[T] ← y // 情況1:如果 “x的父親” 是空節(jié)點(diǎn),則將y設(shè)為根節(jié)點(diǎn)
07 else if x = left[p[x]]
08 then left[p[x]] ← y // 情況2:如果 x是它父節(jié)點(diǎn)的左孩子,則將y設(shè)為“x的父節(jié)點(diǎn)的左孩子”
09 else right[p[x]] ← y // 情況3:(x是它父節(jié)點(diǎn)的右孩子) 將y設(shè)為“x的父節(jié)點(diǎn)的右孩子”
10 left[y] ← x // 將 “x” 設(shè)為 “y的左孩子”
11 p[x] ← y // 將 “x的父節(jié)點(diǎn)” 設(shè)為 “y”
理解上面的代碼之后,下面以一個(gè)更鮮明的圖對(duì)左旋轉(zhuǎn)進(jìn)行說明。理解左旋之后,下面的推理應(yīng)該非常簡單,這里就不過多說明。
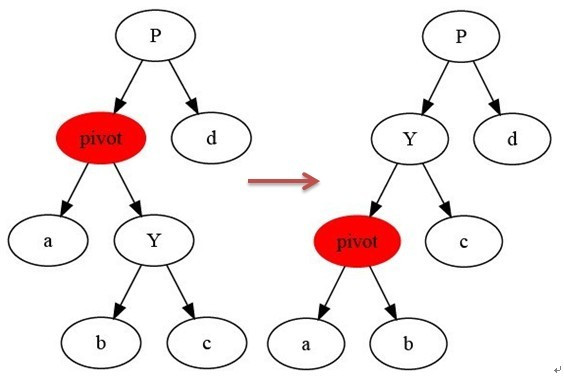
3.2 右旋
右旋和左旋是相對(duì)的,原理類似。理解左旋后,右旋也很容易理解了。

上面是《算法導(dǎo)論》中右旋的示意圖。
參考上面的示意圖和下面的偽代碼,理解“紅黑樹T的節(jié)點(diǎn)y進(jìn)行右旋”是如何進(jìn)行的。
RIGHT-ROTATE(T, y)
01 x ← left[y] // 前提:這里假設(shè)y的左孩子為x。下面開始正式操作
02 left[y] ← right[x] // 將 “x的右孩子” 設(shè)為 “y的左孩子”,即 將β設(shè)為y的左孩子
03 p[right[x]] ← y // 將 “y” 設(shè)為 “x的右孩子的父親”,即 將β的父親設(shè)為y
04 p[x] ← p[y] // 將 “y的父親” 設(shè)為 “x的父親”
05 if p[y] = nil[T]
06 then root[T] ← x // 情況1:如果 “y的父親” 是空節(jié)點(diǎn),則將x設(shè)為根節(jié)點(diǎn)
07 else if y = right[p[y]]
08 then right[p[y]] ← x // 情況2:如果 y是它父節(jié)點(diǎn)的右孩子,則將x設(shè)為“y的父節(jié)點(diǎn)的左孩子”
09 else left[p[y]] ← x // 情況3:(y是它父節(jié)點(diǎn)的左孩子) 將x設(shè)為“y的父節(jié)點(diǎn)的左孩子”
10 right[x] ← y // 將 “y” 設(shè)為 “x的右孩子”
11 p[y] ← x // 將 “y的父節(jié)點(diǎn)” 設(shè)為 “x”
理解上面的代碼之后,下面以一個(gè)更鮮明的圖對(duì)右旋轉(zhuǎn)進(jìn)行說明。
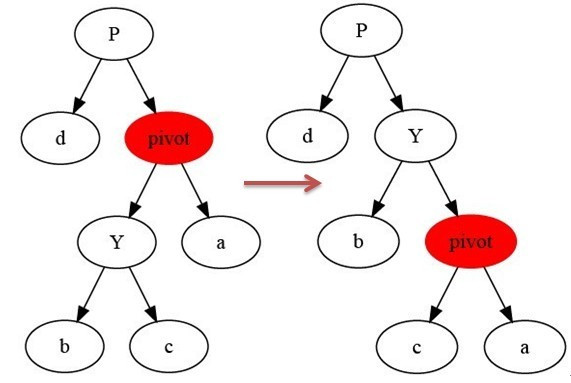
旋轉(zhuǎn)總結(jié):
(01) 左旋 和 右旋 是相對(duì)的兩個(gè)概念,原理類似。理解一個(gè)也就理解了另一個(gè)。
(02) 下面談?wù)勅绾螀^(qū)分 左旋 和 右旋。
在實(shí)際應(yīng)用中,若沒有徹底理解 左旋 和 右旋,可能會(huì)將它們混淆。下面談?wù)勎覍?duì)如何區(qū)分 左旋 和 右旋 的理解。
3.3 區(qū)分 左旋 和 右旋
無論 左旋 或 右旋,它們都是以某一個(gè)節(jié)點(diǎn)為中心點(diǎn)。注意:這里,我們理解成以節(jié)點(diǎn)(節(jié)點(diǎn)x)進(jìn)行旋轉(zhuǎn),而不是以一個(gè)分支(分支xy軸 或 分支xz軸)進(jìn)行旋轉(zhuǎn)!!!
我們以圖來進(jìn)行說明。
左旋示例圖(以x為節(jié)點(diǎn)進(jìn)行左旋):
z
x /
/ \ --(左旋)--> x
y z /
y對(duì)x進(jìn)行左旋,意味著,將“x的右孩子”設(shè)為“x的父親節(jié)點(diǎn)”;即,將 x變成了一個(gè)左節(jié)點(diǎn)(x成了為z的左孩子)!。 因此,左旋中的“左”,意味著“被旋轉(zhuǎn)的節(jié)點(diǎn)將變成一個(gè)左節(jié)點(diǎn)”。
右旋示例圖(以x為節(jié)點(diǎn)進(jìn)行右旋):
y
x \
/ \ --(右旋)--> x
y z \
z對(duì)x進(jìn)行右旋,意味著,將“x的左孩子”設(shè)為“x的父親節(jié)點(diǎn)”;即,將 x變成了一個(gè)右節(jié)點(diǎn)(x成了為y的右孩子)! 因此,右旋中的“右”,意味著“被旋轉(zhuǎn)的節(jié)點(diǎn)將變成一個(gè)右節(jié)點(diǎn)”。
3.4 添加操作
向一顆含有n個(gè)節(jié)點(diǎn)的紅黑樹中插入一個(gè)節(jié)點(diǎn),可以在時(shí)間O(lgn)內(nèi)完成。
將節(jié)點(diǎn)z插入紅黑樹T內(nèi)。需要執(zhí)行的操作依次時(shí):首先,將T當(dāng)作一顆二叉樹,將z插入;然后,將z著色為紅色;最后,通過RB-INSERT-FIXUP來對(duì)節(jié)點(diǎn)重新著色并旋轉(zhuǎn),以此來保證刪除節(jié)點(diǎn)后的樹仍然是一顆紅黑樹。
(01) 將T當(dāng)作一顆二叉樹,將z插入。
因?yàn)榧t黑樹本身就是一顆二叉樹,所以,我們可以根據(jù)二叉樹的性質(zhì)將z插入。
(02) 將z著色為紅色。
在介紹為什么將則著色為紅色之前,我們重新溫習(xí)一下紅黑樹的特性:
(1)每個(gè)節(jié)點(diǎn)或者是黑色,或者是紅色。
(2)根節(jié)點(diǎn)是黑色。
(3)每個(gè)葉子節(jié)點(diǎn)(NIL)是黑色。 [注意:這里葉子節(jié)點(diǎn),是指為空(NIL或NULL)的葉子節(jié)點(diǎn)!]
(4)如果一個(gè)節(jié)點(diǎn)是紅色的,則它的子節(jié)點(diǎn)必須是黑色的。
(5)從一個(gè)節(jié)點(diǎn)到該節(jié)點(diǎn)的子孫節(jié)點(diǎn)的所有路徑上包含相同數(shù)目的黑節(jié)點(diǎn)。
將插入的節(jié)點(diǎn)著色為紅色,不會(huì)違背“特性(5)”;而若將插入的節(jié)點(diǎn)著色為黑色,會(huì)違背該特性。
(03) 通過RB-INSERT-FIXUP來對(duì)節(jié)點(diǎn)重新著色并旋轉(zhuǎn)。
因?yàn)?02)中插入一個(gè)紅色節(jié)點(diǎn)之后,雖然沒有違背“特性(5)”,但是卻可能違背了其它特性(例如,若被插入節(jié)點(diǎn)的父節(jié)點(diǎn)也是紅色;插入后,則違背了“特性(4)”)。我們需要通過RB-INSERT-FIXUP進(jìn)行節(jié)點(diǎn)顏色的調(diào)整以及旋轉(zhuǎn)等工作,讓樹仍然是一顆紅黑樹。
下面是《算法導(dǎo)論》中 “向紅黑樹T中插入節(jié)點(diǎn)z”的偽代碼
RB-INSERT(T, z)
01 y ← nil[T] // 新建節(jié)點(diǎn)“y”,將y設(shè)為空節(jié)點(diǎn)。
02 x ← root[T] // 設(shè)“紅黑樹T”的根節(jié)點(diǎn)為“x”
03 while x ≠ nil[T] // 找出要插入的節(jié)點(diǎn)“z”在二叉樹T中的位置“y”
04 do y ← x
05 if key[z] < key[x]
06 then x ← left[x]
07 else x ← right[x]
08 p[z] ← y // 設(shè)置 “z的父親” 為 “y”
09 if y = nil[T]
10 then root[T] ← z // 情況1:若y是空節(jié)點(diǎn),則將z設(shè)為根
11 else if key[z] < key[y]
12 then left[y] ← z // 情況2:若“z所包含的值” < “y所包含的值”,則將z設(shè)為“y的左孩子”
13 else right[y] ← z // 情況3:(“z所包含的值” >= “y所包含的值”)將z設(shè)為“y的右孩子”
14 left[z] ← nil[T] // z的左孩子設(shè)為空
15 right[z] ← nil[T] // z的右孩子設(shè)為空。至此,已經(jīng)完成將“節(jié)點(diǎn)z插入到二叉樹”中了。
16 color[z] ← RED // 將z著色為“紅色”
17 RB-INSERT-FIXUP(T, z) // 通過RB-INSERT-FIXUP對(duì)紅黑樹的節(jié)點(diǎn)進(jìn)行顏色修改以及旋轉(zhuǎn),讓樹T仍然是一顆紅黑樹
結(jié)合偽代碼以及為代碼上面的說明,先理解RB-INSERT。理解了RB-INSERT之后,我們接著對(duì) RB-INSERT-FIXUP的偽代碼進(jìn)行說明

RB-INSERT-FIXUP(T, z)
01 while color[p[z]] = RED // 若“當(dāng)前節(jié)點(diǎn)(z)的父節(jié)點(diǎn)是紅色”,則進(jìn)行以下處理。
02 do if p[z] = left[p[p[z]]] // 若“z的父節(jié)點(diǎn)”是“z的祖父節(jié)點(diǎn)的左孩子”,則進(jìn)行以下處理。
03 then y ← right[p[p[z]]] // 將y設(shè)置為“z的叔叔節(jié)點(diǎn)(z的祖父節(jié)點(diǎn)的右孩子)”
04 if color[y] = RED // Case 1條件:叔叔是紅色
05 then color[p[z]] ← BLACK ▹ Case 1 // (01) 將“父節(jié)點(diǎn)”設(shè)為黑色。
06 color[y] ← BLACK ▹ Case 1 // (02) 將“叔叔節(jié)點(diǎn)”設(shè)為黑色。
07 color[p[p[z]]] ← RED ▹ Case 1 // (03) 將“祖父節(jié)點(diǎn)”設(shè)為“紅色”。
08 z ← p[p[z]] ▹ Case 1 // (04) 將“祖父節(jié)點(diǎn)”設(shè)為“當(dāng)前節(jié)點(diǎn)”(紅色節(jié)點(diǎn))
09 else if z = right[p[z]] // Case 2條件:叔叔是黑色,且當(dāng)前節(jié)點(diǎn)是右孩子
10 then z ← p[z] ▹ Case 2 // (01) 將“父節(jié)點(diǎn)”作為“新的當(dāng)前節(jié)點(diǎn)”。
11 LEFT-ROTATE(T, z) ▹ Case 2 // (02) 以“新的當(dāng)前節(jié)點(diǎn)”為支點(diǎn)進(jìn)行左旋。
12 color[p[z]] ← BLACK ▹ Case 3 // Case 3條件:叔叔是黑色,且當(dāng)前節(jié)點(diǎn)是左孩子。(01) 將“父節(jié)點(diǎn)”設(shè)為“黑色”。
13 color[p[p[z]]] ← RED ▹ Case 3 // (02) 將“祖父節(jié)點(diǎn)”設(shè)為“紅色”。
14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3 // (03) 以“祖父節(jié)點(diǎn)”為支點(diǎn)進(jìn)行右旋。
15 else (same as then clause with "right" and "left" exchanged) // 若“z的父節(jié)點(diǎn)”是“z的祖父節(jié)點(diǎn)的右孩子”,將上面的操作中“right”和“left”交換位置,然后依次執(zhí)行。
16 color[root[T]] ← BLACK

總的來說:當(dāng)節(jié)點(diǎn)z被著色為紅色節(jié)點(diǎn),并插入二叉樹時(shí),有三種情況。
情況一:被插入的節(jié)點(diǎn)是根節(jié)點(diǎn)。
直接把此節(jié)點(diǎn)涂為黑色。
情況二:被插入的節(jié)點(diǎn)的父節(jié)點(diǎn)是黑色。
什么也不需要做。節(jié)點(diǎn)被插入后,仍然是紅黑樹。
情況三:被插入的節(jié)點(diǎn)的父節(jié)點(diǎn)是紅色。
那么,該情況與紅黑樹的“特性(5)”相沖突。情況三包含了“Case 1”、“Case 2” 和“Case 3”三種情況,情況三的目的是恢復(fù)紅黑樹的特性,它的處理思想是:將紅色的節(jié)點(diǎn)移到根節(jié)點(diǎn);然后,將根節(jié)點(diǎn)設(shè)為黑色。下面介紹情況三的三種情況。
Case 1:叔叔是紅色
Case 1 現(xiàn)象說明:當(dāng)前節(jié)點(diǎn)的父節(jié)點(diǎn)是紅色,且當(dāng)前節(jié)點(diǎn)的祖父節(jié)點(diǎn)的另一個(gè)子節(jié)點(diǎn)(叔叔節(jié)點(diǎn))也是紅色。
Case 1 處理策略:
(01) 將“父節(jié)點(diǎn)”設(shè)為黑色。
(02) 將“叔叔節(jié)點(diǎn)”設(shè)為黑色。
(03) 將“祖父節(jié)點(diǎn)”設(shè)為“紅色”。
(04) 將“祖父節(jié)點(diǎn)”設(shè)為“當(dāng)前節(jié)點(diǎn)”(紅色節(jié)點(diǎn));即,之后繼續(xù)對(duì)“當(dāng)前節(jié)點(diǎn)”進(jìn)行操作。
下面談?wù)劄槭裁匆@樣處理。(建議理解的時(shí)候,通過下面的圖進(jìn)行對(duì)比)
“當(dāng)前節(jié)點(diǎn)”和“父節(jié)點(diǎn)”都是紅色,違背“特性(4)”。所以,將“父節(jié)點(diǎn)”設(shè)置“黑色”以解決這個(gè)問題。
但是,將“父節(jié)點(diǎn)”由“紅色”變成“黑色”之后,違背了“特性(5)”:因?yàn)椋?#8220;父節(jié)點(diǎn)”的分支的黑色節(jié)點(diǎn)的總數(shù)增加了1。 解決這個(gè)問題的辦法是:將“祖父節(jié)點(diǎn)”由“黑色”變成紅色,同時(shí),將“叔叔節(jié)點(diǎn)”由“紅色”變成“黑色”。關(guān)于這里,說明幾點(diǎn):第一,為什么“祖父節(jié)點(diǎn)”之前是黑色?這個(gè)應(yīng)該很容易想明白,因?yàn)樵谧儞Q操作之前,該樹是紅黑樹,“父節(jié)點(diǎn)”是紅色,那么“祖父節(jié)點(diǎn)”一定是黑色。 第二,為什么將“祖父節(jié)點(diǎn)”由“黑色”變成紅色,同時(shí),將“叔叔節(jié)點(diǎn)”由“紅色”變成“黑色”;能解決“包含‘父節(jié)點(diǎn)’的分支的黑色節(jié)點(diǎn)的總數(shù)增加了1”的問題。這個(gè)道理也很簡單。“包含‘父節(jié)點(diǎn)’的分支的黑色節(jié)點(diǎn)的總數(shù)增加了1” 同時(shí)也意味著 “包含‘祖父節(jié)點(diǎn)’的分支的黑色節(jié)點(diǎn)的總數(shù)增加了1”,既然這樣,我們通過將“祖父節(jié)點(diǎn)”由“黑色”變成“紅色”以解決“包含‘祖父節(jié)點(diǎn)’的分支的黑色節(jié)點(diǎn)的總數(shù)增加了1”的問題; 但是,這樣處理之后又會(huì)引起另一個(gè)問題“包含‘叔叔’節(jié)點(diǎn)的分支的黑色節(jié)點(diǎn)的總數(shù)減少了1”,現(xiàn)在我們已知“叔叔節(jié)點(diǎn)”是“紅色”,將“叔叔節(jié)點(diǎn)”設(shè)為“黑色”就能解決這個(gè)問題。 所以,將“祖父節(jié)點(diǎn)”由“黑色”變成紅色,同時(shí),將“叔叔節(jié)點(diǎn)”由“紅色”變成“黑色”;就解決了該問題。
按照上面的步驟處理之后:當(dāng)前節(jié)點(diǎn)、父節(jié)點(diǎn)、叔叔節(jié)點(diǎn)之間都不會(huì)違背紅黑樹特性,但祖父節(jié)點(diǎn)卻不一定。若此時(shí),祖父節(jié)點(diǎn)是根節(jié)點(diǎn),直接將祖父節(jié)點(diǎn)設(shè)為“黑色”,那就完全解決這個(gè)問題了;若祖父節(jié)點(diǎn)不是根節(jié)點(diǎn),那我們需要將“祖父節(jié)點(diǎn)”設(shè)為“新的當(dāng)前節(jié)點(diǎn)”,接著對(duì)“新的當(dāng)前節(jié)點(diǎn)”進(jìn)行分析。
Case 1 處理前[當(dāng)前節(jié)點(diǎn)是4]:
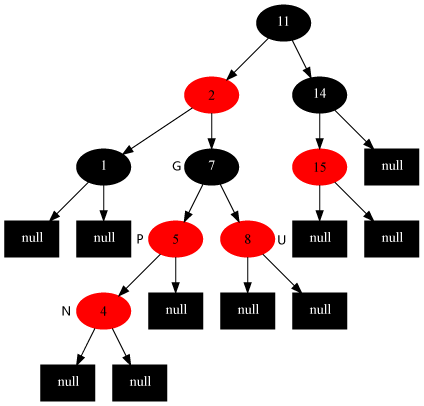
Case 1 處理后:
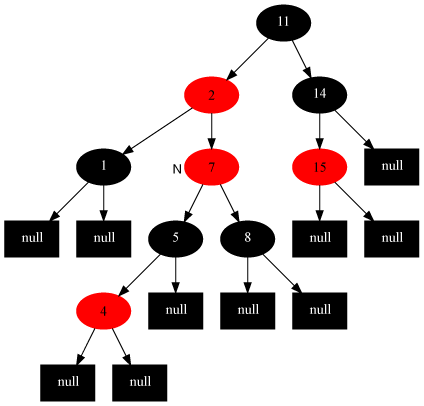
Case 2:叔叔是黑色,且當(dāng)前節(jié)點(diǎn)是右孩子
Case 2 現(xiàn)象說明:當(dāng)前節(jié)點(diǎn)的父節(jié)點(diǎn)是紅色,叔叔節(jié)點(diǎn)是黑色,且當(dāng)前節(jié)點(diǎn)是其父節(jié)點(diǎn)的右孩子
Case 2 處理策略:
(01) 將“父節(jié)點(diǎn)”作為“新的當(dāng)前節(jié)點(diǎn)”。
(02) 以“新的當(dāng)前節(jié)點(diǎn)”為支點(diǎn)進(jìn)行左旋。
下面談?wù)劄槭裁匆@樣處理。(建議理解的時(shí)候,通過下面的圖進(jìn)行對(duì)比)
首先,將“父節(jié)點(diǎn)”作為“新的當(dāng)前節(jié)點(diǎn)”;接著,以“新的當(dāng)前節(jié)點(diǎn)”為支點(diǎn)進(jìn)行左旋。 為了便于理解,我們先說明第(02)步,再說明第(01)步;為了便于說明,我們?cè)O(shè)置“父節(jié)點(diǎn)”的代號(hào)為F(Father),“當(dāng)前節(jié)點(diǎn)”的代號(hào)為S(Son)。
為什么要“以F為支點(diǎn)進(jìn)行左旋”呢?根據(jù)已知條件可知:S是F的右孩子。而之前我們說過,我們處理紅黑樹的核心思想:將紅色的節(jié)點(diǎn)移到根節(jié)點(diǎn);然后,將根節(jié)點(diǎn)設(shè)為黑色。既然是“將紅色的節(jié)點(diǎn)移到根節(jié)點(diǎn)”,那就是說要不斷的將破壞紅黑樹特性的紅色節(jié)點(diǎn)上移(即向根方向移動(dòng))。 而S又是一個(gè)右孩子,因此,我們可以通過“左旋”來將S上移!
按照上面的步驟(以F為支點(diǎn)進(jìn)行左旋)處理之后:若S變成了根節(jié)點(diǎn),那么直接將其設(shè)為“黑色”,就完全解決問題了;若S不是根節(jié)點(diǎn),那我們需要執(zhí)行步驟(01),即“將F設(shè)為‘新的當(dāng)前節(jié)點(diǎn)’”。那為什么不繼續(xù)以S為新的當(dāng)前節(jié)點(diǎn)繼續(xù)處理,而需要以F為新的當(dāng)前節(jié)點(diǎn)來進(jìn)行處理呢?這是因?yàn)?#8220;左旋”之后,F(xiàn)變成了S的“子節(jié)點(diǎn)”,即S變成了F的父節(jié)點(diǎn);而我們處理問題的時(shí)候,需要從下至上(由葉到根)方向進(jìn)行處理;也就是說,必須先解決“孩子”的問題,再解決“父親”的問題;所以,我們執(zhí)行步驟(01):將“父節(jié)點(diǎn)”作為“新的當(dāng)前節(jié)點(diǎn)”。
Case 2 處理前[當(dāng)前節(jié)點(diǎn)是7]:
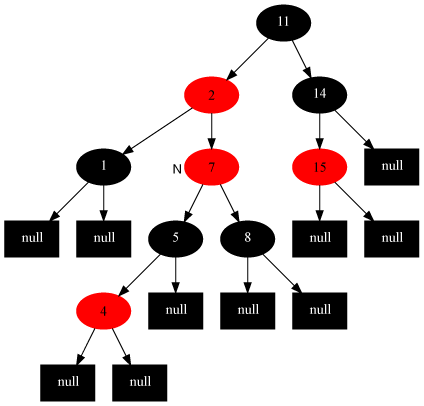
Case 2處理后:
Case 3:叔叔是黑色,且當(dāng)前節(jié)點(diǎn)是左孩子
Case 3:叔叔是黑色,且當(dāng)前節(jié)點(diǎn)是左孩子
Case 3 現(xiàn)象說明:當(dāng)前節(jié)點(diǎn)的父節(jié)點(diǎn)是紅色,叔叔節(jié)點(diǎn)是黑色,且當(dāng)前節(jié)點(diǎn)是其父節(jié)點(diǎn)的左孩子
Case 3 處理策略:
(01) 將“父節(jié)點(diǎn)”設(shè)為“黑色”。
(02) 將“祖父節(jié)點(diǎn)”設(shè)為“紅色”。
(03) 以“祖父節(jié)點(diǎn)”為支點(diǎn)進(jìn)行右旋。
下面談?wù)劄槭裁匆@樣處理。(建議理解的時(shí)候,通過下面的圖進(jìn)行對(duì)比)
為了便于說明,我們?cè)O(shè)置“當(dāng)前節(jié)點(diǎn)”為S(Original Son),“兄弟節(jié)點(diǎn)”為B(Brother),“叔叔節(jié)點(diǎn)”為U(Uncle),“父節(jié)點(diǎn)”為F(Father),祖父節(jié)點(diǎn)為G(Grand-Father)。
S和F都是紅色,違背了紅黑樹的“特性(4)”,我們可以將F由“紅色”變?yōu)?#8220;黑色”,就解決了“違背‘特性(4)’”的問題;但卻引起了其它問題:違背特性(5),因?yàn)閷由紅色改為黑色之后,所有經(jīng)過F的分支的黑色節(jié)點(diǎn)的個(gè)數(shù)增加了1。那我們?nèi)绾谓鉀Q“所有經(jīng)過F的分支的黑色節(jié)點(diǎn)的個(gè)數(shù)增加了1”的問題呢? 我們可以通過“將G由黑色變成紅色”,同時(shí)“以G為支點(diǎn)進(jìn)行右旋”來解決。
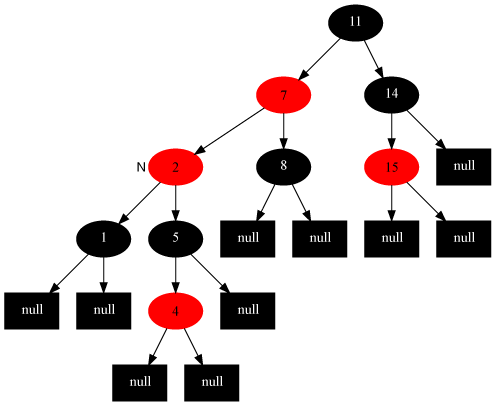
Case 3 處理前[當(dāng)前節(jié)點(diǎn)是2]:
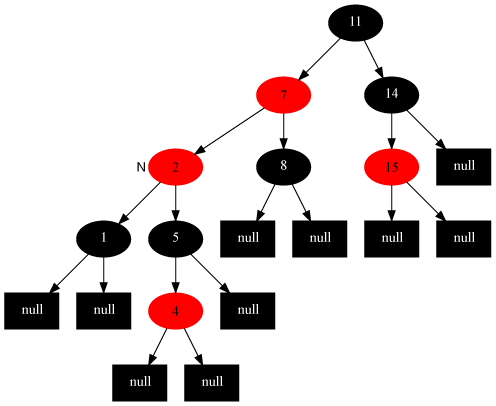
Case 3 處理后:
3.5 刪除操作
將紅黑樹T內(nèi)的節(jié)點(diǎn)z刪除。需要執(zhí)行的操作依次是:首先,將T當(dāng)作一顆二叉樹,將節(jié)點(diǎn)刪除;然后,通過RB-DELETE-FIXUP來對(duì)節(jié)點(diǎn)重新著色并旋轉(zhuǎn),以此來保證刪除節(jié)點(diǎn)后的樹仍然是一顆紅黑樹。
(01) 將T當(dāng)作一顆二叉樹,將節(jié)點(diǎn)刪除。
這和"刪除常規(guī)二叉搜索樹中刪除節(jié)點(diǎn)的方法是一樣的"。分3種情況:
第一種,被刪除節(jié)點(diǎn)沒有兒子,即為葉節(jié)點(diǎn)。那么,直接將該節(jié)點(diǎn)刪除就OK了。
第二種,被刪除節(jié)點(diǎn)只有一個(gè)兒子。那么,直接刪除該節(jié)點(diǎn),并用該節(jié)點(diǎn)的唯一子節(jié)點(diǎn)頂替它的位置。
第三種,被刪除節(jié)點(diǎn)有兩個(gè)兒子。那么,首先把“它的后繼節(jié)點(diǎn)的內(nèi)容”復(fù)制給“該節(jié)點(diǎn)的內(nèi)容”;之后,刪除“它的后繼節(jié)點(diǎn)”。
這里有兩點(diǎn)需要說明:第一步中復(fù)制時(shí),僅僅復(fù)制內(nèi)容,即將“它的后繼節(jié)點(diǎn)的內(nèi)容”復(fù)制給“該節(jié)點(diǎn)的內(nèi)容”。 這相當(dāng)于用“該節(jié)點(diǎn)的后繼節(jié)點(diǎn)”取代“該節(jié)點(diǎn)”,之后就刪除“該節(jié)點(diǎn)的后繼節(jié)點(diǎn)”即可,而不需要?jiǎng)h除“該節(jié)點(diǎn)”(因?yàn)?#8220;該節(jié)點(diǎn)”已經(jīng)被“它的后繼節(jié)點(diǎn)”所取代)。
第二步中刪除“該節(jié)點(diǎn)的后繼節(jié)點(diǎn)”時(shí),需要注意:“該節(jié)點(diǎn)的后繼節(jié)點(diǎn)”不可能是雙子非空,這個(gè)根據(jù)二叉樹的特性可知。 既然“該節(jié)點(diǎn)的后繼節(jié)點(diǎn)”不可能雙子都非空,就意味著“該節(jié)點(diǎn)的后繼節(jié)點(diǎn)”要么沒有兒子,要么只有一個(gè)兒子。若沒有兒子,則按“第一種”種的辦法進(jìn)行處理;若只有一個(gè)兒子,則按“第二種”中的辦法進(jìn)行處理。
(02) 通過RB-DELETE-FIXUP來對(duì)節(jié)點(diǎn)重新著色并旋轉(zhuǎn),以此來保證刪除節(jié)點(diǎn)后的樹仍然是一顆紅黑樹。
因?yàn)?01)中刪除節(jié)點(diǎn)之后,可能會(huì)違背紅黑樹的特性。所以需要,通過RB-DELETE-FIXUP來重新校正,為當(dāng)前樹保持紅黑樹的特性。
下面是《算法導(dǎo)論》中 “從紅黑樹T中刪除節(jié)點(diǎn)z”的偽代碼
RB-DELETE(T, z)
01 if left[z] = nil[T] or right[z] = nil[T]
02 then y ← z // 若“z的左孩子” 或 “z的右孩子”為空,則將“z”賦值給 “y”;
03 else y ← TREE-SUCCESSOR(z) // 否則,將“z的后繼節(jié)點(diǎn)”賦值給 “y”。
04 if left[y] ≠ nil[T]
05 then x ← left[y] // 若“y的左孩子” 不為空,則將“y的左孩子” 賦值給 “x”;
06 else x ← right[y] // 否則,“y的右孩子” 賦值給 “x”。
07 p[x] ← p[y] // 將“y的父節(jié)點(diǎn)” 設(shè)置為 “x的父節(jié)點(diǎn)”
08 if p[y] = nil[T]
09 then root[T] ← x // 情況1:若“y的父節(jié)點(diǎn)” 為空,則設(shè)置“x” 為 “根節(jié)點(diǎn)”。
10 else if y = left[p[y]]
11 then left[p[y]] ← x // 情況2:若“y是它父節(jié)點(diǎn)的左孩子”,則設(shè)置“x” 為 “y的父節(jié)點(diǎn)的左孩子”
12 else right[p[y]] ← x // 情況3:若“y是它父節(jié)點(diǎn)的右孩子”,則設(shè)置“x” 為 “y的父節(jié)點(diǎn)的右孩子”
13 if y ≠ z
14 then key[z] ← key[y] // 若“y的值” 賦值給 “z”。注意:這里只拷貝z的值給y,而沒有拷貝z的顏色!!!
15 copy y's satellite data into z
16 if color[y] = BLACK
17 then RB-DELETE-FIXUP(T, x) // 若“y為黑節(jié)點(diǎn)”,則調(diào)用
18 return y
結(jié)合偽代碼以及為代碼上面的說明,先理解RB-DELETE。理解了RB-DELETE之后,接著對(duì) RB-DELETE-FIXUP的偽代碼進(jìn)行說明

RB-DELETE-FIXUP(T, x)
01 while x ≠ root[T] and color[x] = BLACK
02 do if x = left[p[x]]
03 then w ← right[p[x]] // 若 “x”是“它父節(jié)點(diǎn)的左孩子”,則設(shè)置 “w”為“x的叔叔”(即x為它父節(jié)點(diǎn)的右孩子)
04 if color[w] = RED // Case 1: x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是紅色。(此時(shí)x的父節(jié)點(diǎn)和x的兄弟節(jié)點(diǎn)的子節(jié)點(diǎn)都是黑節(jié)點(diǎn))。
05 then color[w] ← BLACK ▹ Case 1 // (01) 將x的兄弟節(jié)點(diǎn)設(shè)為“黑色”。
06 color[p[x]] ← RED ▹ Case 1 // (02) 將x的父節(jié)點(diǎn)設(shè)為“紅色”。
07 LEFT-ROTATE(T, p[x]) ▹ Case 1 // (03) 對(duì)x的父節(jié)點(diǎn)進(jìn)行左旋。
08 w ← right[p[x]] ▹ Case 1 // (04) 左旋后,重新設(shè)置x的兄弟節(jié)點(diǎn)。
09 if color[left[w]] = BLACK and color[right[w]] = BLACK // Case 2: x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是黑色,x的兄弟節(jié)點(diǎn)的兩個(gè)孩子都是黑色。
10 then color[w] ← RED ▹ Case 2 // (01) 將x的兄弟節(jié)點(diǎn)設(shè)為“紅色”。
11 x ← p[x] ▹ Case 2 // (02) 設(shè)置“x的父節(jié)點(diǎn)”為“新的x節(jié)點(diǎn)”。
12 else if color[right[w]] = BLACK // Case 3: x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是黑色;x的兄弟節(jié)點(diǎn)的左孩子是紅色,右孩子是黑色的。
13 then color[left[w]] ← BLACK ▹ Case 3 // (01) 將x兄弟節(jié)點(diǎn)的左孩子設(shè)為“黑色”。
14 color[w] ← RED ▹ Case 3 // (02) 將x兄弟節(jié)點(diǎn)設(shè)為“紅色”。
15 RIGHT-ROTATE(T, w) ▹ Case 3 // (03) 對(duì)x的兄弟節(jié)點(diǎn)進(jìn)行右旋。
16 w ← right[p[x]] ▹ Case 3 // (04) 右旋后,重新設(shè)置x的兄弟節(jié)點(diǎn)。
17 color[w] ← color[p[x]] ▹ Case 4 // Case 4: x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是黑色;x的兄弟節(jié)點(diǎn)的右孩子是紅色的。(01) 將x父節(jié)點(diǎn)顏色 賦值給 x的兄弟節(jié)點(diǎn)。
18 color[p[x]] ← BLACK ▹ Case 4 // (02) 將x父節(jié)點(diǎn)設(shè)為“黑色”。
19 color[right[w]] ← BLACK ▹ Case 4 // (03) 將x兄弟節(jié)點(diǎn)的右子節(jié)設(shè)為“黑色”。
20 LEFT-ROTATE(T, p[x]) ▹ Case 4 // (04) 對(duì)x的父節(jié)點(diǎn)進(jìn)行左旋。
21 x ← root[T] ▹ Case 4 // (05) 設(shè)置“x”為“根節(jié)點(diǎn)”。
22 else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父節(jié)點(diǎn)的右孩子”,將上面的操作中“right”和“left”交換位置,然后依次執(zhí)行。
23 color[x] ← BLACK

在開始說明RB-DELETE-FIXUP之前,我們?cè)俅螠亓?xí)一下紅黑樹的幾個(gè)特性:
(1)每個(gè)節(jié)點(diǎn)或者是黑色,或者是紅色。
(2)根節(jié)點(diǎn)是黑色。
(3)每個(gè)葉子節(jié)點(diǎn)(NIL)是黑色。 [注意:這里葉子節(jié)點(diǎn),是指為空(NIL或NULL)的葉子節(jié)點(diǎn)!]
(4)如果一個(gè)節(jié)點(diǎn)是紅色的,則它的子節(jié)點(diǎn)必須是黑色的。
(5)從一個(gè)節(jié)點(diǎn)到該節(jié)點(diǎn)的子孫節(jié)點(diǎn)的所有路徑上包含相同數(shù)目的黑節(jié)點(diǎn)。
在RB-DELETE中,若被刪除的節(jié)點(diǎn)y是黑色的,則會(huì)產(chǎn)生三個(gè)問題。
問題一:如y是根節(jié)點(diǎn),而刪除y后,它的紅色孩子成了新的根節(jié)點(diǎn),則違反了“特性(2)”。
問題二:如x和“y的父節(jié)點(diǎn)”都是紅色,則違反了“特性(4)”。因?yàn)閯h除y之后,“y的父節(jié)點(diǎn)”和“x”是父子關(guān)系。
問題三:刪除y,意味著刪除了一個(gè)黑色節(jié)點(diǎn),那么“之前所有包含y的路徑上的黑節(jié)點(diǎn)總數(shù)減少了1”,這違反了“特性(5)”。
合計(jì)起來,違反了“特性(2)、(4)、(5)”三個(gè)特性。
RB-DELETE-FIXUP需要解決上面的三個(gè)問題,進(jìn)而保持紅黑樹的全部特性。
為了便于分析,我們假設(shè)“x包含一個(gè)額外的黑色”(x原本的顏色還存在),這樣就不會(huì)違反“特性(5)”。為什么呢?
通過RB-DELETE算法,我們知道:刪除節(jié)點(diǎn)y之后,x占據(jù)了原來節(jié)點(diǎn)y的位置。 既然刪除y(y是黑色),意味著減少一個(gè)黑色節(jié)點(diǎn);那么,再在該位置上增加一個(gè)黑色即可。這樣,當(dāng)我們假設(shè)“x包含一個(gè)額外的黑色”,就正好彌補(bǔ)了“刪除y所丟失的黑色節(jié)點(diǎn)”,也就不會(huì)違反“特性(5)”。 因此,假設(shè)“x包含一個(gè)額外的黑色”(x原本的顏色還存在),這樣就不會(huì)違反“特性(5)”。
現(xiàn)在,x不僅包含它原本的顏色屬性,x還包含一個(gè)額外的黑色。即x的顏色屬性是“紅+黑”或“黑+黑”,它違反了“特性(1)”。
現(xiàn)在,我們面臨的問題,由解決“違反了特性(2)、(4)、(5)三個(gè)特性”轉(zhuǎn)換成了“解決違反特性(1)、(2)、(4)三個(gè)特性”。
RB-DELETE-FIXUP就是通過算法恢復(fù)紅黑樹的特性(1)、(2)、(4)。RB-DELETE-FIXUP的思想是:將x所包含的額外的黑色不斷沿樹上移(向根方向移動(dòng)),直到:
(01) x指向一個(gè)“紅+黑”節(jié)點(diǎn)。此時(shí),將x設(shè)為一個(gè)“黑”節(jié)點(diǎn)即可。
(02) x指向根。此時(shí),將x設(shè)為一個(gè)“黑”節(jié)點(diǎn)即可。
(03) 做必要的旋轉(zhuǎn)和顏色修改。
將上面的思想,可以概括為3種情況。
情況一:x是“紅+黑”節(jié)點(diǎn)。
直接把x設(shè)為黑色,結(jié)束。此時(shí)紅黑樹性質(zhì)全部恢復(fù)。
情況二:x是“黑+黑”節(jié)點(diǎn),且x是根。
什么都不做,結(jié)束。此時(shí)紅黑樹性質(zhì)全部恢復(fù)。
情況三:x是“黑+黑”節(jié)點(diǎn),且x不是根。這又可以劃分了4種情況:Case 1、Case 2、Case 3、Case 4。
Case 1
Case 1 現(xiàn)象說明:x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是紅色。(此時(shí)x的父節(jié)點(diǎn)和x的兄弟節(jié)點(diǎn)的子節(jié)點(diǎn)都是黑節(jié)點(diǎn))。
Case 1 處理策略:
(01) 將x的兄弟節(jié)點(diǎn)設(shè)為“黑色”。
(02) 將x的父節(jié)點(diǎn)設(shè)為“紅色”。
(03) 對(duì)x的父節(jié)點(diǎn)進(jìn)行左旋。
(04) 左旋后,重新設(shè)置x的兄弟節(jié)點(diǎn)。
下面談?wù)劄槭裁匆@樣處理。(建議理解的時(shí)候,通過下面的圖進(jìn)行對(duì)比)
這樣做的目的是將“Case 1”轉(zhuǎn)換為“Case 2”、“Case 3”或“Case 4”,從而進(jìn)行進(jìn)一步的處理。對(duì)x的父節(jié)點(diǎn)進(jìn)行左旋;左旋后,為了保持紅黑樹特性,就需要在左旋前“將x的兄弟節(jié)點(diǎn)設(shè)為黑色”,同時(shí)“將x的父節(jié)點(diǎn)設(shè)為紅色”;左旋后,由于x的兄弟節(jié)點(diǎn)發(fā)生了變化,需要更新x的兄弟節(jié)點(diǎn),從而進(jìn)行后續(xù)處理。
Case 1 處理前[當(dāng)前節(jié)點(diǎn)是A]:
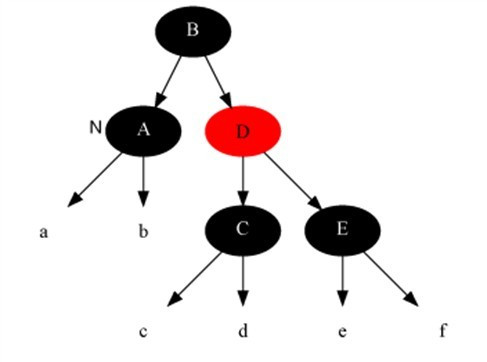
Case 1 處理后:
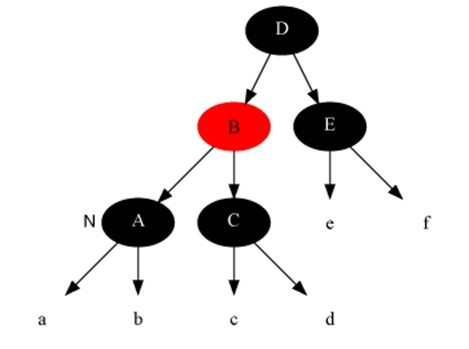
Case 2
Case 2 現(xiàn)象說明:x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是黑色,x的兄弟節(jié)點(diǎn)的兩個(gè)孩子都是黑色。
Case 2 處理策略:
(01) 將x的兄弟節(jié)點(diǎn)設(shè)為“紅色”。
(02) 設(shè)置“x的父節(jié)點(diǎn)”為“新的x節(jié)點(diǎn)”。
下面談?wù)劄槭裁匆@樣處理。(建議理解的時(shí)候,通過下面的圖進(jìn)行對(duì)比)
這個(gè)情況的處理思想:是將“x中多余的一個(gè)黑色屬性上移(往根方向移動(dòng))”。 x是“黑+黑”節(jié)點(diǎn),我們將x由“黑+黑”節(jié)點(diǎn) 變成 “黑”節(jié)點(diǎn),多余的一個(gè)“黑”屬性移到x的父節(jié)點(diǎn)中,即x的父節(jié)點(diǎn)多出了一個(gè)黑屬性(若x的父節(jié)點(diǎn)原先是“黑”,則此時(shí)變成了“黑+黑”;若x的父節(jié)點(diǎn)原先時(shí)“紅”,則此時(shí)變成了“紅+黑”)。 此時(shí),需要注意的是:所有經(jīng)過x的分支中黑節(jié)點(diǎn)個(gè)數(shù)沒變化;但是,所有經(jīng)過x的兄弟節(jié)點(diǎn)的分支中黑色節(jié)點(diǎn)的個(gè)數(shù)增加了1(因?yàn)閤的父節(jié)點(diǎn)多了一個(gè)黑色屬性)!為了解決這個(gè)問題,我們需要將“所有經(jīng)過x的兄弟節(jié)點(diǎn)的分支中黑色節(jié)點(diǎn)的個(gè)數(shù)減1”即可,那么就可以通過“將x的兄弟節(jié)點(diǎn)由黑色變成紅色”來實(shí)現(xiàn)。
經(jīng)過上面的步驟(將x的兄弟節(jié)點(diǎn)設(shè)為紅色),多余的一個(gè)顏色屬性(黑色)已經(jīng)跑到x的父節(jié)點(diǎn)中。我們需要將x的父節(jié)點(diǎn)設(shè)為“新的x節(jié)點(diǎn)”進(jìn)行處理。若“新的x節(jié)點(diǎn)”是“黑+紅”,直接將“新的x節(jié)點(diǎn)”設(shè)為黑色,即可完全解決該問題;若“新的x節(jié)點(diǎn)”是“黑+黑”,則需要對(duì)“新的x節(jié)點(diǎn)”進(jìn)行進(jìn)一步處理。
Case 2 處理前[當(dāng)前節(jié)點(diǎn)是A]:
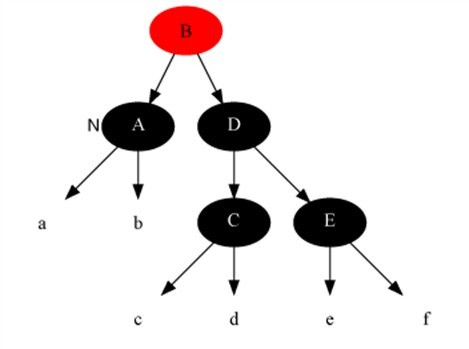
Case 2 處理后:
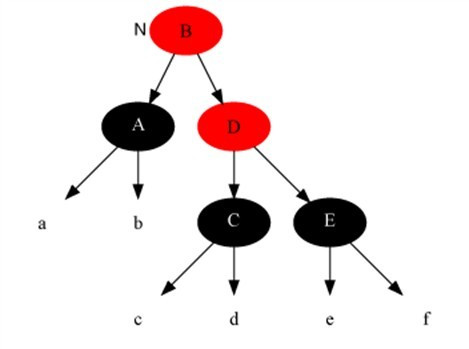
Case 3
Case 3 現(xiàn)象說明:x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是黑色;x的兄弟節(jié)點(diǎn)的左孩子是紅色,右孩子是黑色的。
Case 3 處理策略:
(01) 將x兄弟節(jié)點(diǎn)的左孩子設(shè)為“黑色”。
(02) 將x兄弟節(jié)點(diǎn)設(shè)為“紅色”。
(03) 對(duì)x的兄弟節(jié)點(diǎn)進(jìn)行右旋。
(04) 右旋后,重新設(shè)置x的兄弟節(jié)點(diǎn)。
下面談?wù)劄槭裁匆@樣處理。(建議理解的時(shí)候,通過下面的圖進(jìn)行對(duì)比)
我們處理“Case 3”的目的是為了將“Case 3”進(jìn)行轉(zhuǎn)換,轉(zhuǎn)換成“Case 4”,從而進(jìn)行進(jìn)一步的處理。轉(zhuǎn)換的方式是對(duì)x的兄弟節(jié)點(diǎn)進(jìn)行右旋;為了保證右旋后,它仍然是紅黑樹,就需要在右旋前“將x的兄弟節(jié)點(diǎn)的左孩子設(shè)為黑色”,同時(shí)“將x的兄弟節(jié)點(diǎn)設(shè)為紅色”;右旋后,由于x的兄弟節(jié)點(diǎn)發(fā)生了變化,需要更新x的兄弟節(jié)點(diǎn),從而進(jìn)行后續(xù)處理。
Case 3 處理前[當(dāng)前節(jié)點(diǎn)是A]:
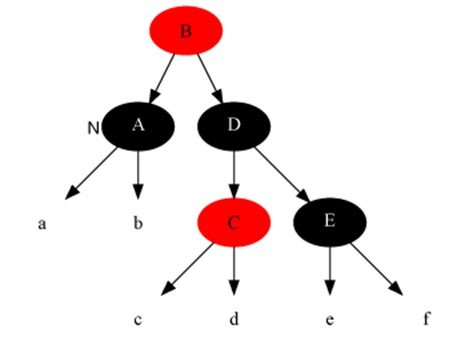
Case 3 處理后:
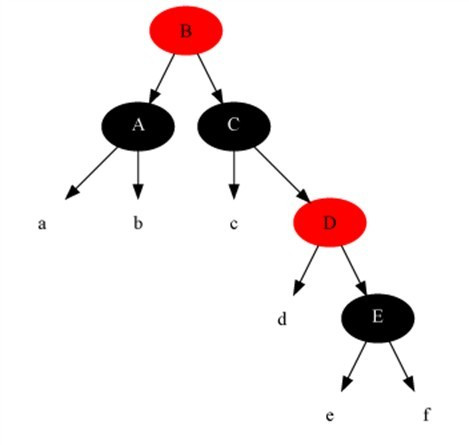
Case 4
Case 4 現(xiàn)象說明:x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是黑色;x的兄弟節(jié)點(diǎn)的左孩子是紅色,右孩子是黑色的。
Case 4 現(xiàn)象說明:x是“黑+黑”節(jié)點(diǎn),x的兄弟節(jié)點(diǎn)是黑色;x的兄弟節(jié)點(diǎn)的右孩子是紅色的。
Case 4 處理策略:
(01) 將x父節(jié)點(diǎn)顏色 賦值給 x的兄弟節(jié)點(diǎn)。
(02) 將x父節(jié)點(diǎn)設(shè)為“黑色”。
(03) 將x兄弟節(jié)點(diǎn)的右子節(jié)設(shè)為“黑色”。
(04) 對(duì)x的父節(jié)點(diǎn)進(jìn)行左旋。
(05) 設(shè)置“x”為“根節(jié)點(diǎn)”。
下面談?wù)劄槭裁匆@樣處理。(建議理解的時(shí)候,通過下面的圖進(jìn)行對(duì)比)
我們處理“Case 4”的目的是:去掉x中額外的黑色,將x變成單獨(dú)的黑色。處理的方式是“:進(jìn)行顏色修改,然后對(duì)x的父節(jié)點(diǎn)進(jìn)行左旋。下面,我們來分析是如何實(shí)現(xiàn)的。
為了便于說明,我們?cè)O(shè)置“當(dāng)前節(jié)點(diǎn)”為S(Original Son),“兄弟節(jié)點(diǎn)”為B(Brother),“兄弟節(jié)點(diǎn)的左孩子”為BLS(Brother's Left Son),“兄弟節(jié)點(diǎn)的右孩子”為BRS(Brother's Right Son),“父節(jié)點(diǎn)”為F(Father)。
我們要對(duì)F進(jìn)行左旋。但在左旋前,我們需要調(diào)換F和B的顏色,并設(shè)置BRS為黑色。為什么需要這里處理呢?因?yàn)樽笮螅現(xiàn)和BLS是父子關(guān)系,而我們已知BL是紅色,如果F是紅色,則違背了“特性(4)”;為了解決這一問題,我們將“F設(shè)置為黑色”。 但是,F(xiàn)設(shè)置為黑色之后,為了保證滿足“特性(5)”,即為了保證左旋之后:
第一,“同時(shí)經(jīng)過根節(jié)點(diǎn)和S的分支的黑色節(jié)點(diǎn)個(gè)數(shù)不變”。
若滿足“第一”,只需要S丟棄它多余的顏色即可。因?yàn)镾的顏色是“黑+黑”,而左旋后“同時(shí)經(jīng)過根節(jié)點(diǎn)和S的分支的黑色節(jié)點(diǎn)個(gè)數(shù)”增加了1;現(xiàn)在,只需將S由“黑+黑”變成單獨(dú)的“黑”節(jié)點(diǎn),即可滿足“第一”。
第二,“同時(shí)經(jīng)過根節(jié)點(diǎn)和BLS的分支的黑色節(jié)點(diǎn)數(shù)不變”。
若滿足“第二”,只需要將“F的原始顏色”賦值給B即可。之前,我們已經(jīng)將“F設(shè)置為黑色”(即,將B的顏色"黑色",賦值給了F)。至此,我們算是調(diào)換了F和B的顏色。
第三,“同時(shí)經(jīng)過根節(jié)點(diǎn)和BRS的分支的黑色節(jié)點(diǎn)數(shù)不變”。
在“第二”已經(jīng)滿足的情況下,若要滿足“第三”,只需要將BRS設(shè)置為“黑色”即可。
經(jīng)過,上面的處理之后。紅黑樹的特性全部得到的滿足!接著,我們將x設(shè)為根節(jié)點(diǎn),就可以跳出while循環(huán)(參考偽代碼);即完成了全部處理。
至此,我們就完成了Case 4的處理。理解Case 4的核心,是了解如何“去掉當(dāng)前節(jié)點(diǎn)額外的黑色”。
Case 4 處理前[當(dāng)前節(jié)點(diǎn)是A]:
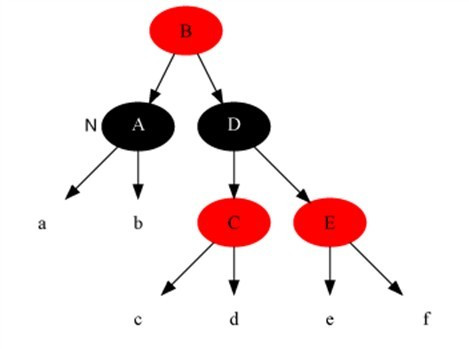
Case 4 處理后:
OK!至此,紅黑樹的理論知識(shí)差不多講完了。后續(xù)再更新紅黑樹的實(shí)現(xiàn)代碼!
參考文獻(xiàn)
1, 《算法導(dǎo)論》
2, 教你透徹了解紅黑樹