強(qiáng)烈推薦此題!
一種巧妙的DP,稱為插頭DP。每個格子是一個階段,狀態(tài)是通過這個格子的右邊一個格子的左邊和上邊的S形折線(共由m+1條線段組成)上的3進(jìn)制數(shù)。
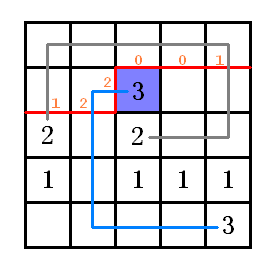
這是題目的第一個sample,我把行、列都從1開始編號,原始圖設(shè)為g,紅線表示狀態(tài)f[2][2][(100221)3]。
狀態(tài)設(shè)計好了,狀態(tài)轉(zhuǎn)移也就不是難事了。根據(jù)g[i][j + 1]的值來確定狀態(tài)轉(zhuǎn)移的方式。
我是用順推的轉(zhuǎn)移,不大好表述,不懂的話看看代碼,再看看圖,想想就能明白。

 /**//*************************************************************************
/**//*************************************************************************
 Author: WHU_GCC
Author: WHU_GCC
 Created Time: 2007-9-24 19:35:22
Created Time: 2007-9-24 19:35:22
 File Name: pku3133.cpp
File Name: pku3133.cpp
 Description:
Description:
 ************************************************************************/
************************************************************************/
 #include <iostream>
#include <iostream>
 using namespace std;
using namespace std;

 #define out(x) (cout << #x << ": " << x << endl)
#define out(x) (cout << #x << ": " << x << endl)
 typedef long long int64;
typedef long long int64;
 const int maxint = 0x7FFFFFFF;
const int maxint = 0x7FFFFFFF;
 const int64 maxint64 = 0x7FFFFFFFFFFFFFFFLL;
const int64 maxint64 = 0x7FFFFFFFFFFFFFFFLL;

 template <class T> void show(T a, int n)
template <class T> void show(T a, int n)  { for (int i = 0; i < n; ++i) cout << a[i] << ' '; cout << endl; }
{ for (int i = 0; i < n; ++i) cout << a[i] << ' '; cout << endl; }

 template <class T> void show(T a, int r, int l)
template <class T> void show(T a, int r, int l)  { for (int i = 0; i < r; ++i) show(a[i], l); cout << endl; }
{ for (int i = 0; i < r; ++i) show(a[i], l); cout << endl; }

 const int maxn = 10;
const int maxn = 10;

 const int mask[11] =
const int mask[11] =  {1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 59049};
{1, 3, 9, 27, 81, 243, 729, 2187, 6561, 19683, 59049};

 int g[maxn][maxn];
int g[maxn][maxn];
 char f[maxn + 1][maxn][59049];
char f[maxn + 1][maxn][59049];
 int n, m;
int n, m;
 int pow3m;
int pow3m;

 inline int get_bit(int x, int k)
inline int get_bit(int x, int k)


 {
{
 return x % mask[k + 1] / mask[k];
return x % mask[k + 1] / mask[k];
 }
}

 inline int set_bit(int x, int k)
inline int set_bit(int x, int k)


 {
{
 return x - get_bit(x, k) * mask[k] - get_bit(x, k + 1) * mask[k + 1];
return x - get_bit(x, k) * mask[k] - get_bit(x, k + 1) * mask[k + 1];
 }
}

 int dp()
int dp()


 {
{
 pow3m = mask[m + 1];
pow3m = mask[m + 1];
 memset(f, 0x7F, sizeof(f));
memset(f, 0x7F, sizeof(f));
 f[1][0][0] = 0;
f[1][0][0] = 0;
 for (int i = 1; i <= n; i++)
for (int i = 1; i <= n; i++)


 {
{
 for (int j = 0; j < m; j++)
for (int j = 0; j < m; j++)
 for (int k = 0; k < pow3m; k++) if (f[i][j][k] != 0x7F)
for (int k = 0; k < pow3m; k++) if (f[i][j][k] != 0x7F)


 {
{
 int bit_j = get_bit(k, j);
int bit_j = get_bit(k, j);
 int bit_j1 = get_bit(k , j + 1);
int bit_j1 = get_bit(k , j + 1);
 int pre_bit = set_bit(k, j);
int pre_bit = set_bit(k, j);
 if (g[i][j + 1] == 1)
if (g[i][j + 1] == 1)


 {
{
 if (bit_j == 0 && bit_j1 == 0)
if (bit_j == 0 && bit_j1 == 0)
 f[i][j + 1][k] <?= f[i][j][k];
f[i][j + 1][k] <?= f[i][j][k];
 }
}
 else if (g[i][j + 1] == 2)
else if (g[i][j + 1] == 2)


 {
{
 if (bit_j + bit_j1 == 1)
if (bit_j + bit_j1 == 1)
 f[i][j + 1][pre_bit] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit] <?= f[i][j][k] + 1;
 if (bit_j + bit_j1 == 0)
if (bit_j + bit_j1 == 0)


 {
{
 f[i][j + 1][pre_bit + mask[j]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + mask[j]] <?= f[i][j][k] + 1;
 f[i][j + 1][pre_bit + mask[j + 1]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + mask[j + 1]] <?= f[i][j][k] + 1;
 }
}
 }
}
 else if (g[i][j + 1] == 3)
else if (g[i][j + 1] == 3)


 {
{
 if (bit_j == 0 && bit_j1 == 2 || bit_j == 2 && bit_j1 == 0)
if (bit_j == 0 && bit_j1 == 2 || bit_j == 2 && bit_j1 == 0)
 f[i][j + 1][pre_bit] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit] <?= f[i][j][k] + 1;
 if (bit_j + bit_j1 == 0)
if (bit_j + bit_j1 == 0)


 {
{
 f[i][j + 1][pre_bit + 2 * mask[j]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + 2 * mask[j]] <?= f[i][j][k] + 1;
 f[i][j + 1][pre_bit + 2 * mask[j + 1]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + 2 * mask[j + 1]] <?= f[i][j][k] + 1;
 }
}
 }
}
 else
else


 {
{
 if (bit_j == 1 && bit_j1 == 0 || bit_j == 0 && bit_j1 == 1)
if (bit_j == 1 && bit_j1 == 0 || bit_j == 0 && bit_j1 == 1)


 {
{
 f[i][j + 1][pre_bit + mask[j]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + mask[j]] <?= f[i][j][k] + 1;
 f[i][j + 1][pre_bit + mask[j + 1]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + mask[j + 1]] <?= f[i][j][k] + 1;
 }
}
 if (bit_j == 0 && bit_j1 == 2 || bit_j == 2 && bit_j1 == 0)
if (bit_j == 0 && bit_j1 == 2 || bit_j == 2 && bit_j1 == 0)


 {
{
 f[i][j + 1][pre_bit + 2 * mask[j]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + 2 * mask[j]] <?= f[i][j][k] + 1;
 f[i][j + 1][pre_bit + 2 * mask[j + 1]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + 2 * mask[j + 1]] <?= f[i][j][k] + 1;
 }
}
 if (bit_j == 1 && bit_j1 == 1 || bit_j + bit_j1 == 4)
if (bit_j == 1 && bit_j1 == 1 || bit_j + bit_j1 == 4)
 f[i][j + 1][pre_bit] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit] <?= f[i][j][k] + 1;
 if (bit_j + bit_j1 == 0)
if (bit_j + bit_j1 == 0)


 {
{
 f[i][j + 1][pre_bit] <?= f[i][j][k];
f[i][j + 1][pre_bit] <?= f[i][j][k];
 f[i][j + 1][pre_bit + mask[j] + mask[j + 1]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + mask[j] + mask[j + 1]] <?= f[i][j][k] + 1;
 f[i][j + 1][pre_bit + 2 * mask[j] + 2 * mask[j + 1]] <?= f[i][j][k] + 1;
f[i][j + 1][pre_bit + 2 * mask[j] + 2 * mask[j + 1]] <?= f[i][j][k] + 1;
 }
}
 }
}
 }
}
 for (int k = 0; k < pow3m / 3; k++)
for (int k = 0; k < pow3m / 3; k++)
 f[i + 1][0][k * 3] = f[i][m][k];
f[i + 1][0][k * 3] = f[i][m][k];
 }
}
 if (f[n][m][0] == 0x7F)
if (f[n][m][0] == 0x7F)
 return 0;
return 0;
 else
else
 return f[n][m][0] - 2;
return f[n][m][0] - 2;
 }
}

 int main()
int main()


 {
{
 while (scanf("%d%d", &n, &m), n + m != 0)
while (scanf("%d%d", &n, &m), n + m != 0)


 {
{
 for (int i = 1; i <= n; i++)
for (int i = 1; i <= n; i++)
 for (int j = 1; j <= m; j++)
for (int j = 1; j <= m; j++)
 scanf("%d", &g[i][j]);
scanf("%d", &g[i][j]);
 printf("%d\n", dp());
printf("%d\n", dp());
 }
}
 return 0;
return 0;
 }
}