1、二叉搜索樹(shù)是二叉樹(shù)的一種,樹(shù)的每個(gè)結(jié)點(diǎn)含有一個(gè)數(shù)據(jù)項(xiàng),每個(gè)數(shù)據(jù)項(xiàng)有一個(gè)鍵值。結(jié)點(diǎn)的存儲(chǔ)位置是由鍵值的大小決定的,所以二叉搜索樹(shù)是關(guān)聯(lián)式容器。
(1)、 若它的左子樹(shù)不空,則左子樹(shù)上所有結(jié)點(diǎn)的鍵值均小于它的根結(jié)點(diǎn)的鍵值;
(2)、若它的右子樹(shù)不空,則右子樹(shù)上所有結(jié)點(diǎn)的鍵值均大于它的根結(jié)點(diǎn)的鍵值;
(3)、它的左、右子樹(shù)也分別為二叉排序樹(shù)。
注意:::二叉排序樹(shù)是一種
動(dòng)態(tài)樹(shù)表,樹(shù)的結(jié)構(gòu)通常不是一次生成的。而是在查找的過(guò)程中,當(dāng)樹(shù)中不存在關(guān)鍵字等于給定值的節(jié)點(diǎn)時(shí)再進(jìn)行插入。新插入的結(jié)點(diǎn)一定是一個(gè)新添加的
葉子結(jié)點(diǎn),并且是查找不成功時(shí)查找路徑上訪問(wèn)的最后一個(gè)結(jié)點(diǎn)的左孩子或右孩子結(jié)點(diǎn)。
2、插入與查找算法:
查找:
(1)、若二叉排序樹(shù)非空,將給定值與根節(jié)點(diǎn)的關(guān)鍵字值比較,若相等,則查找成功;
(2)、若不等,則當(dāng)根節(jié)點(diǎn)的關(guān)鍵字值大于給定值時(shí),到根的左子樹(shù)中進(jìn)行查找;
(3)、否則到根的右子樹(shù)中進(jìn)行查找。若找到,則查找過(guò)程是走了一條從樹(shù)根到所找到節(jié)點(diǎn)的路徑;
(4)、否則,查找過(guò)程終止于一棵空樹(shù)。
//① 、普通查找,查找不成功返回NULL
遞歸思想:
BiTree SearchBST (BiTree *T,KeyType key)
{
//在根指針T所指二叉排序樹(shù)中遞歸地查找某關(guān)鍵字等于key的數(shù)據(jù)元素
//若查找成功,則返回指向該數(shù)據(jù)元素結(jié)點(diǎn)的指針,否則返回空指針
if( (!T)||(key==T—>data.key))
return (T); //查找結(jié)束,此時(shí)T為NULL,或者為該結(jié)點(diǎn)
else if (key< T—>data.key)
return(SearchBST(T—>lchild,key)); //在左子樹(shù)中繼續(xù)查找
else
return(SearchBST(T —>rchild,key));// 在右子樹(shù)中繼續(xù)查找
}//SearchBST
非遞歸思想:
BiTree SearchBST (BiTree *root,KeyType key)
{
BiTree *p;
if( root == NULL)return NULL;//查找結(jié)束,此時(shí)根為NULL,
p = root;
while(p!=NULL)
{
if(p ->key==Key)breat;
if( Key < p ->key) p =p ->lchild;//在左子樹(shù)中繼續(xù)查找
else p = p ->rchild;//在右子樹(shù)中繼續(xù)查找
}
return p;
}
//② 、查找不成功,返回插入位置
//在根指針T所指二叉排序樹(shù)中遞歸地查找其關(guān)鍵字等于key的數(shù)據(jù)元素,
//若查找成功,則指針p指向該數(shù)據(jù)元素結(jié)點(diǎn),并返回TRUE,
//否則指針p指向查找路徑上訪問(wèn)的最后一個(gè)結(jié)點(diǎn)并返回FALSE,
//指針f指向T的雙親,其初始調(diào)用值為NULL
BOOL SearchBST(BiTree *T,KeyType key,BiTree *f,BiTree &p)
{
if(!T) {p=f;return FALSE;} //查找不成功
else if (key==T—>data.key)
{p=T;return TRUE;} //查找成功
else if (key<T—>data.key) SearchBST(T—>lchild,key,T,p); //在左子樹(shù)中繼續(xù)查找
else SearchBST(T—>rchild,key,T,p);//在右子樹(shù)中繼續(xù)查找
}//SearchBST
插入:
(1)、首先執(zhí)行查找算法,找出被插結(jié)點(diǎn)的父親結(jié)點(diǎn)。沒(méi)找到則新建子結(jié)點(diǎn)
(2)、判斷被插結(jié)點(diǎn)是其父親結(jié)點(diǎn)的左、右兒子。將被插結(jié)點(diǎn)作為葉子結(jié)點(diǎn)插入。
(3)、若二叉樹(shù)為空。則首先單獨(dú)生成根結(jié)點(diǎn)
基于BOOL SearchBST(BiTree *T,KeyType key,BiTree *f,BiTree &p)的插入算法
相當(dāng)于新建子樹(shù)。
//當(dāng)二叉排序樹(shù)T中不存在關(guān)鍵字等于e.key的數(shù)據(jù)元素時(shí),插入e并返回TRUE,否則返回FALSE
Status Insert BST(BiTree &T,ElemType e)
{
if(!SearchBST(T,e.key,NULL,p) ) //返回P為插入的結(jié)點(diǎn)點(diǎn)
{ //先查找,不成功新建結(jié)點(diǎn)
s=(BiTree)malloc(sizeof(BiTNode));
s->data=e; s->lchild= s->rchild=NULL;
if (!p) T = s; //被插結(jié)點(diǎn)*s為新的根結(jié)點(diǎn) ,原樹(shù)為空
else if (e.key<p->data.key) p->lchild=s; //被插結(jié)點(diǎn)*s為左孩子
else p—>rchild=s //被插結(jié)點(diǎn)*s為右孩子
return TRUE;
}
else
return FALSE; //樹(shù)中已有關(guān)鍵字相同的結(jié)點(diǎn),不再插入
}// Insert BST
void InsertBST(BSTree *Tptr,KeyType key)
{
//若二叉排序樹(shù) *Tptr中沒(méi)有關(guān)鍵字為key,則插入,否則直接返回
BSTNode *f,*p=*TPtr; //p的初值指向根結(jié)點(diǎn)
while(p){ //查找插入位置
if(p->key==key) return;//樹(shù)中已有key,無(wú)須插入
f=p; //f保存當(dāng)前查找的結(jié)點(diǎn)
p=(key<p->key)?p->lchild:p->rchild;
//若key<p->key,則在左子樹(shù)中查找,否則在右子樹(shù)中查找
} //endwhile
//f為插入的結(jié)點(diǎn)
p=(BSTNode *)malloc(sizeof(BSTNode));
p->key=key; p->lchild=p->rchild=NULL; //生成新結(jié)點(diǎn)
if(*TPtr==NULL) //原樹(shù)為空
*Tptr=p; //新插入的結(jié)點(diǎn)為新的根
else //原樹(shù)非空時(shí)將新結(jié)點(diǎn)關(guān)p作為關(guān)f的左孩子或右孩子插入
if(key<f->key)
f->lchild=p;
else f->rchild=p;
} //InsertBST4、刪除算法
①刪除操作的一般步驟
(1) 進(jìn)行查找
查找時(shí),令p指向當(dāng)前訪問(wèn)到的結(jié)點(diǎn),parent指向其雙親(其初值為NULL)。若樹(shù)中找不到被刪結(jié)點(diǎn)則返回,否則被刪結(jié)點(diǎn)是*p。
(2) 刪去*p。
刪*p時(shí),應(yīng)將*p的子樹(shù)(若有)仍連接在樹(shù)上且保持BST性質(zhì)不變。按*p的孩子數(shù)目分三種情況進(jìn)行處理。
②刪除*p結(jié)點(diǎn)的三種情況(1)*p是葉子(即它的孩子數(shù)為0)
無(wú)須連接*p的子樹(shù),只需將*p的雙親*parent中指向*p的指針域置空即可。
(2)*p只有一個(gè)孩子*child
只需將*child和*p的雙親直接連接后,即可刪去*p。
注意: *p既可能是*parent的左孩子也可能是其右孩子,而*child可能是*p的左孩子或右孩子,故共有4種狀態(tài)。
(3)*p有兩個(gè)孩子
先令q=p,將被刪結(jié)點(diǎn)的地址保存在q中;然后找*q的中序后繼*p,并在查找過(guò)程中仍用parent記住*p的雙親位置。*q的中序后繼*p一定是*q的右子樹(shù)中最左下的結(jié)點(diǎn),它無(wú)左子樹(shù)。因此,可以將刪去*q的操作轉(zhuǎn)換為刪去的*p的操作,即在釋放結(jié)點(diǎn)*p之前將其數(shù)據(jù)復(fù)制到*q中,就相當(dāng)于刪去了*q。
③二叉排序樹(shù)刪除算法
分析:
上述三種情況都能統(tǒng)一到情況(2),算法中只需針對(duì)情況(2)處理即可。
注意邊界條件:若parent為空,被刪結(jié)點(diǎn)*p是根,故刪去*p后,應(yīng)將child置為根。
算法:刪除關(guān)鍵字為key的結(jié)點(diǎn)
void DelBSTNode(BSTree *Tptr,KeyType key)
{
//在二叉排序樹(shù)*Tptr中刪去關(guān)鍵字為key的結(jié)點(diǎn)
BSTNode *parent=NUll,*p=*Tptr,*q,*child;
while(p)
{
//從根開(kāi)始查找關(guān)鍵字為key的待刪結(jié)點(diǎn)
if(p->key==key) break;//已找到,跳出查找循環(huán)
parent=p; //parent指向*p的雙親
p=(key<p->key)?p->lchild:p->rchild; //在關(guān)p的左或右子樹(shù)中繼續(xù)找
}
//注意:也可以使用基于BOOL SearchBST(BiTree *T,KeyType key,BiTree *f,BiTree &p)的查找算法
//結(jié)果是 parent 記錄了要?jiǎng)h除結(jié)點(diǎn)的父結(jié)點(diǎn),p指向要?jiǎng)h除的結(jié)點(diǎn)
if(!p) return; //找不到被刪結(jié)點(diǎn)則返回
q=p; //q記住被刪結(jié)點(diǎn)*p
if(q->lchild && q->rchild) //*q的兩個(gè)孩子均非空,故找*q的中序后繼*p
for(parent=q,p=q->rchild; p->lchild; parent=p,p=p=->lchild);
//現(xiàn)在情況(3)已被轉(zhuǎn)換為情況(2),而情況(1)相當(dāng)于是情況(2)中child=NULL的狀況
child=(p->lchild)?p->lchild:p->rchild;//若是情況(2),則child非空;否則child為空
if(!parent) //*p的雙親為空,說(shuō)明*p為根,刪*p后應(yīng)修改根指針
*Tptr=child; //若是情況(1),則刪去*p后,樹(shù)為空;否則child變?yōu)楦?br /> else{ //*p不是根,將*p的孩子和*p的雙親進(jìn)行連接,*p從樹(shù)上被摘下
if(p==parent->lchild) //*p是雙親的左孩子
parent->lchild=child; //*child作為*parent的左孩子
else parent->rchild=child; //*child作為 parent的右孩子
if(p!=q) //是情況(3),需將*p的數(shù)據(jù)復(fù)制到*q
q->key=p->key; //若還有其它數(shù)據(jù)域亦需復(fù)制
} //endif
free(p); /釋放*p占用的空間
} //DelBSTNode
給出三種情況的不同算法
第一種:
btree * DelNode(btree *p)
{
if (p->lchild)
{
btree *r = p->lchild; //r指向其左子樹(shù);
while(r->rchild != NULL)//搜索左子樹(shù)的最右邊的葉子結(jié)點(diǎn)r
{
r = r->rchild;
}
r->rchild = p->rchild;
btree *q = p->lchild; //q指向其左子樹(shù);
free(p);
return q;
}
else
{
btree *q = p->rchild; //q指向其右子樹(shù);
free(p);
return q;
}
}
第二種:
btree * DelNode(btree *p)
{
if (p->lchild)
{
btree *r = p->lchild; //r指向其左子樹(shù);
btree *prer = p->lchild; //prer指向其左子樹(shù);
while(r->rchild != NULL)//搜索左子樹(shù)的最右邊的葉子結(jié)點(diǎn)r
{
prer = r;
r = r->rchild;
}
if(prer != r)//若r不是p的左孩子,把r的左孩子作為r的父親的右孩子
{
prer->rchild = r->lchild;
r->lchild = p->lchild; //被刪結(jié)點(diǎn)p的左子樹(shù)作為r的左子樹(shù)
}
r->rchild = p->rchild; //被刪結(jié)點(diǎn)p的右子樹(shù)作為r的右子樹(shù)
free(p);
return r;
}
else
{
btree *q = p->rchild; //q指向其右子樹(shù);
free(p);
return q;
}
}
哈夫曼樹(shù)定義為:給定n個(gè)權(quán)值作為n個(gè)葉子結(jié)點(diǎn),構(gòu)造一棵二叉樹(shù),若帶權(quán)路徑長(zhǎng)度達(dá)到最小,稱這樣的二叉樹(shù)為最優(yōu)二叉樹(shù),也稱為哈夫曼樹(shù)(Huffman tree)。
1、那么什么是權(quán)值?什么是路徑長(zhǎng)度?什么是帶權(quán)路徑長(zhǎng)度呢?
權(quán)值:哈夫曼樹(shù)的權(quán)值是自己定義的,他的物理意義表示數(shù)據(jù)出現(xiàn)的次數(shù)、頻率。可以用樹(shù)的每個(gè)結(jié)點(diǎn)數(shù)據(jù)域data存放一個(gè)特定的數(shù)表示它的值。
路徑長(zhǎng)度:在一棵樹(shù)中,從一個(gè)結(jié)點(diǎn)往下可以達(dá)到的孩子或子孫結(jié)點(diǎn)之間的通路,稱為路徑。通路中分支的數(shù)目稱為路徑長(zhǎng)度。若規(guī)定根結(jié)點(diǎn)的層數(shù)為1,則從根結(jié)點(diǎn)到第L層結(jié)點(diǎn)的路徑長(zhǎng)度為L(zhǎng)-1。
結(jié)點(diǎn)的帶權(quán)路徑長(zhǎng)度為:從根結(jié)點(diǎn)到該結(jié)點(diǎn)之間的路徑長(zhǎng)度與該結(jié)點(diǎn)的權(quán)的乘積。 樹(shù)中所有葉子節(jié)點(diǎn)的帶權(quán)路徑長(zhǎng)度之和,WPL=sigma(w*l)
2、哈夫曼樹(shù)的構(gòu)造過(guò)程。(結(jié)合圖例)
假設(shè)有n個(gè)權(quán)值,則構(gòu)造出的哈夫曼樹(shù)有n個(gè)葉子結(jié)點(diǎn)。 n個(gè)權(quán)值分別設(shè)為 w1、w2、…、wn,則哈夫曼樹(shù)的構(gòu)造規(guī)則為:
(1) 將w1、w2、…,wn看成是有n 棵樹(shù)的森林(每棵樹(shù)僅有一個(gè)結(jié)點(diǎn));
(2) 在森林中選出兩個(gè)根結(jié)點(diǎn)的權(quán)值最小的樹(shù)合并,作為一棵新樹(shù)的左、右子樹(shù),且新樹(shù)的根結(jié)點(diǎn)權(quán)值為其左、右子樹(shù)根結(jié)點(diǎn)權(quán)值之和;
(3)從森林中刪除選取的兩棵樹(shù),并將新樹(shù)加入森林;
(4)重復(fù)(2)、(3)步,直到森林中只剩一棵樹(shù)為止,該樹(shù)即為所求得的哈夫曼樹(shù)
3、哈夫曼樹(shù)的應(yīng)用:哈夫曼編碼(前綴編碼)
哈夫曼編碼
在數(shù)據(jù)通信中,通常需要把要傳送的文字轉(zhuǎn)換為由二進(jìn)制字符0和1組成的二進(jìn)制串,這個(gè)過(guò)程被稱之為編碼(Encoding)。例如,假設(shè)要傳送的電文為DCBBADD,電文中只有A、B、C、D四種字符,若這四個(gè)字符采用表(a)所示的編碼方案,則電文的代碼為11100101001111,代碼總長(zhǎng)度為14。若采用表(b) 所示的編碼方案,則電文的代碼為0110101011100,代碼總長(zhǎng)度為13。

字符集的不同編碼方案
哈夫曼樹(shù)可用于構(gòu)造總長(zhǎng)度最短的編碼方案。具體構(gòu)造方法如下:
設(shè)需要編碼的字符集為{d1,d2,…,dn},各個(gè)字符在電文中出現(xiàn)的次數(shù)或頻率集合為{w1,w2,…,wn}。以d1,d2,…,dn作為葉子結(jié)點(diǎn),以w1,w2,…,wn作為相應(yīng)葉子結(jié)點(diǎn)的權(quán)值來(lái)構(gòu)造一棵哈夫曼樹(shù)。規(guī)定哈夫曼樹(shù)中的左分支代表0,右分支代表1,則從根結(jié)點(diǎn)到葉子結(jié)點(diǎn)所經(jīng)過(guò)的路徑分支組成的0和1的序列便為該結(jié)點(diǎn)對(duì)應(yīng)字符的編碼就是哈夫曼編碼(Huffman Encoding)。
在建立不等長(zhǎng)編碼中,必須使任何一個(gè)字符的編碼都不是另一個(gè)編碼的前綴,這樣才能保證譯碼的唯一性。例如,若字符A的編碼是00,字符B的編碼是001,那么字符A的編碼就成了字符B的編碼的后綴。這樣,對(duì)于代碼串001001,在譯碼時(shí)就無(wú)法判定是將前兩位碼00譯成字符A還是將前三位碼001譯成B。這樣的編碼被稱之為具有二義性的編碼,二義性編碼是不唯一的。而在哈夫曼樹(shù)中,每個(gè)字符結(jié)點(diǎn)都是葉子結(jié)點(diǎn),它們不可能在根結(jié)點(diǎn)到其它字符結(jié)點(diǎn)的路徑上,所以一個(gè)字符的哈夫曼編碼不可能是另一個(gè)字符的哈夫曼編碼的前綴,從而保證了譯碼的非二義性。
下圖就是電文DCBBADD的哈夫曼樹(shù):

4、哈夫曼樹(shù)的實(shí)現(xiàn)
由哈夫曼樹(shù)的構(gòu)造算法可知,用一個(gè)數(shù)組存放原來(lái)的n個(gè)葉子結(jié)點(diǎn)和構(gòu)造過(guò)程中臨時(shí)生成的結(jié)點(diǎn),數(shù)組的大小為2n-1。所以,哈夫曼樹(shù)類HuffmanTree中有兩個(gè)成員字段:data數(shù)組用于存放結(jié)點(diǎn),leafNum表示哈夫曼樹(shù)葉子結(jié)點(diǎn)的數(shù)目。結(jié)點(diǎn)有四個(gè)域,一個(gè)域weight,用于存放該結(jié)點(diǎn)的權(quán)值;一個(gè)域lChild,用于存放該結(jié)點(diǎn)的左孩子結(jié)點(diǎn)在數(shù)組中的序號(hào);一個(gè)域rChild,用于存放該結(jié)點(diǎn)的右孩子結(jié)點(diǎn)在數(shù)組中的序號(hào);一個(gè)域parent,用于判定該結(jié)點(diǎn)是否已加入哈夫曼樹(shù)中。
哈夫曼樹(shù)結(jié)點(diǎn)的結(jié)構(gòu)為:| 數(shù)據(jù) | weight | lChild | rChild | parent |
public class Node
{
char c; //存儲(chǔ)的數(shù)據(jù),為一個(gè)字符
private double weight; //結(jié)點(diǎn)權(quán)值
private int lChild; //左孩子結(jié)點(diǎn)
private int rChild; //右孩子結(jié)點(diǎn)
private int parent; //父結(jié)點(diǎn)
//結(jié)點(diǎn)權(quán)值屬性
public double Weight
{
get
{
return weight;
}
set
{
weight = value;
}
}
//左孩子結(jié)點(diǎn)屬性
public int LChild
{
get
{
return lChild;
}
set
{
lChild = value;
}
}
//右孩子結(jié)點(diǎn)屬性
public int RChild
{
get
{
return rChild;
}
set
{
rChild = value;
}
}
//父結(jié)點(diǎn)屬性
public int Parent
{
get
{
return parent;
}
set
{
parent = value;
}
}
//構(gòu)造器
public Node()
{
weight = 0;
lChild = -1;
rChild = -1;
parent = -1;
}
//構(gòu)造器
public Node(double weitht)
{
this.weight = weitht;
lChild = -1;
rChild = -1;
parent = -1;
}
//構(gòu)造器
public Node(int w, int lc, int rc, int p)
{
weight = w;
lChild = lc;
rChild = rc;
parent = p;
}
}
public class HuffmanTree
{
private Node[] data; //結(jié)點(diǎn)數(shù)組
private int leafNum; //葉子結(jié)點(diǎn)數(shù)目
//索引器
public Node this[int index]
{
get
{
return data[index];
}
set
{
data[index] = value;
}
}
//葉子結(jié)點(diǎn)數(shù)目屬性
public int LeafNum
{
get
{
return leafNum;
}
set
{
leafNum = value;
}
}
//構(gòu)造器
public HuffmanTree(int n)
{
data = new Node[2 * n - 1];
leafNum = n;
}
//創(chuàng)建哈夫曼樹(shù)
public void Create(Node[] datain)
{
double minL, minR;
minL = minR = double.MaxValue;
int lchild, rchild;
lchild = rchild = -1;
int length = data.Length;
//初始化哈夫曼樹(shù)
for (int i = 0; i < length; i++)
data[i] = new Node();
for (int i = 0; i < datain.Length; i++)
data[i] = datain[i];
//處理n個(gè)葉子結(jié)點(diǎn),建立哈夫曼樹(shù)
for (int i = leafNum; i < length; i++)
{
//在全部結(jié)點(diǎn)中找權(quán)值最小的兩個(gè)結(jié)點(diǎn)
for (int j = 0; j < i; j++)
{
if (data[j].Parent == -1)
{
if (data[j].Weight < minL)
{
minR = minL;
minL = data[j].Weight;
rchild = lchild;
lchild = j;
}
else if (data[j].Weight < minR)
{
minR = data[j].Weight;
rchild = j;
}
}
}
data[lchild].Parent = data[rchild].Parent = i;
data[i].Weight = minL + minR;
data[i].LChild = lchild;
data[i].RChild = rchild;
}
}
}
class Program
{
static void Main(string[] args)
{
HuffmanTree tree = new HuffmanTree(5);
Node[] nodes = new Node[] { new Node(1), new Node(2), new Node(2.5d), new Node(3), new Node(2.6d) };
tree.Create(nodes);
Console.ReadLine();
}
}
/////////////////////////////節(jié)選自網(wǎng)絡(luò)上的資料、
優(yōu)先隊(duì)列是不同于先進(jìn)先出隊(duì)列的另一種隊(duì)列。每次從隊(duì)列中取出的是具有
最高優(yōu)先權(quán)的元素。每個(gè)元素都有一個(gè)優(yōu)先權(quán)或值
/////用堆實(shí)現(xiàn)優(yōu)先隊(duì)列
1、把優(yōu)先隊(duì)列中的元素按優(yōu)先級(jí)大小組織成堆,堆頂元素具有最大優(yōu)先級(jí)。
2、優(yōu)先隊(duì)列的插入與刪除可以用堆的插入與刪除實(shí)現(xiàn)。
3、優(yōu)先隊(duì)列在定義為priority_queue ,在STL中#include<queue> 中實(shí)現(xiàn)、
priority_queue<int, vector<int>, greater<int> >qi2;
其中
第二個(gè)參數(shù)為容器類型。
第三個(gè)參數(shù)為比較函數(shù)。
估計(jì)還要問(wèn)問(wèn):什么是堆,什么是堆排序?堆與計(jì)算機(jī)分配內(nèi)存的堆相同嗎?
很多資料給出:堆的定義是
(1)、n個(gè)關(guān)鍵字序列(Kl,K2,…,Kn)稱為(Heap),當(dāng)且僅當(dāng)該序列滿足如下性質(zhì)(簡(jiǎn)稱為堆性質(zhì)):
ki≤K2i且ki≤K2i+1 或 Ki≥K2i且ki≥K2i+1 (1≤i≤ n) //ki相當(dāng)于二叉樹(shù)的非葉結(jié)點(diǎn),K2i則是左孩子,k2i+1是右孩子
(2)若將此序列所存儲(chǔ)的向量R[1..n]看做是一棵
完全二叉樹(shù)的存儲(chǔ)結(jié)構(gòu),則堆實(shí)質(zhì)上是滿足如下性質(zhì)的完全二叉樹(shù):
樹(shù)中任一非葉結(jié)點(diǎn)的關(guān)鍵字均不大于(或不小于)其左右孩子(若存在)結(jié)點(diǎn)的關(guān)鍵字。
(3)、根結(jié)點(diǎn)(亦稱為堆頂)的關(guān)鍵字是堆里所有結(jié)點(diǎn)關(guān)鍵字中
最小者的堆稱為
小根堆,又稱最小堆。根結(jié)點(diǎn)(亦稱為堆頂)的關(guān)鍵字是堆里所有結(jié)點(diǎn)關(guān)鍵字中
最大者,稱為大根堆,又稱
最大堆。
(4)、堆中任一子樹(shù)亦是堆。
(5)、堆可以視為一棵完全的二叉樹(shù),完全二叉樹(shù)的一個(gè)“優(yōu)秀”的性質(zhì)是,除了最底層之外,每一層都是滿的,這使得堆可以利用數(shù)組來(lái)表示(普通的一般的二叉樹(shù)通常用鏈表作為基本容器表示),每一個(gè)結(jié)點(diǎn)對(duì)應(yīng)數(shù)組中的一個(gè)元素。那么堆排序呢?
堆排序其實(shí)就是將一組無(wú)序的序列變成堆的過(guò)程、下面我們一起看看堆排序的算法。
2、堆排序
以最大堆為例,步驟為:
① 先將初始文件R[1..n]建成一個(gè)大根堆,此堆為初始的無(wú)序區(qū)
② 再將關(guān)鍵字最大的記錄R[1](即堆頂)和無(wú)序區(qū)的最后一個(gè)記錄R[n]交換,由此得到新的無(wú)序區(qū)R[1..n-1]和有序區(qū)R[n],且滿足R[1..n-1].keys≤R[n].key
③由于交換后新的根R[1]可能違反堆性質(zhì),故應(yīng)將當(dāng)前無(wú)序區(qū)R[1..n-1]調(diào)整為堆。然后再次將R[1..n-1]中關(guān)鍵字最大的記錄R[1]和該區(qū)間的最后一個(gè)記錄R[n-1]交換,由此得到新的無(wú)序區(qū)R[1..n-2]和有序區(qū)R[n-1..n],且仍滿足關(guān)系R[1..n-2].keys≤R[n-1..n].keys,同樣要將R[1..n-2]調(diào)整為堆。
……
直到無(wú)序區(qū)只有一個(gè)元素為止。
將一個(gè)無(wú)序的序列建成堆的過(guò)程實(shí)際上是一個(gè)反復(fù)篩選的過(guò)程。若將此序列看作是一棵完全二叉樹(shù),則最后一個(gè)非終端結(jié)點(diǎn)是[n/2](不大于n/2的整數(shù)),因此篩選過(guò)程只需從[n/2]開(kāi)始。要建成一個(gè)大頂堆,即先選擇一個(gè)值最大的元素并與序列中的最后一個(gè)元素交換,然后對(duì)序列前n-1元素進(jìn)行篩選,從新調(diào)整為一個(gè)大頂堆,直到結(jié)束。
算法描述如下:
typedef int[] Elem;//采用順序存儲(chǔ)表示完全二叉樹(shù)
void HeapAdjust(Elem &e,int s,int m)
{//e中s...m的元素除e[s]之外已經(jīng)滿足堆的定義(e[i] <=e[2*i]&&e[i] <=e[2*i+1]
//或e[i]> =e[2*i]&&e[i]> =e[2*i+1]),調(diào)整e[s]使的e[s...m]成為一個(gè)大頂堆。
selem=e[s];
for(i=2*s;i <=m;i*=2)//沿著值較大的元素(結(jié)點(diǎn))向下篩選
{
if(i <m && e[i] <e[i+1])++i;//i為值較大的元素下標(biāo)
if(selem> =e[i])break;
e[s]=e[i];
s=i;
}
e[s]=selem;
}
void HeapSort(Elem &e)
{//對(duì)順序表排序
for(i=e.length/2;i> 0;--i)
HeapAdjust(e,i,e.length);
for(i=e.length;i> 1;--i)
{
temp=e[1]; //將堆中的最后一個(gè)元素與第一個(gè)元素交換
e[1]=e[i];
e[i]=temp;
HeapAdjust(H,1,i-1);//調(diào)整1..i-1的元素成為大頂堆
}
}
/////////////////////////////////////////////////////////////
使用堆排序注意的問(wèn)題:::
1、序列是從1開(kāi)始的。,注意定義,R[1..n],故要空出R[0]。
2、堆排序算法分為兩部分:建立大頂堆和排序。
3、排序的最壞時(shí)間復(fù)雜度為
O(nlogn)。堆序的平均性能較接近于最壞性能。
4、由于建初始堆所需的比較次數(shù)較多,所以堆排序不適宜于記錄數(shù)較少的文件。
5、 堆排序是就地排序,輔助空間為O(1), 它是
不穩(wěn)定的排序方法。
問(wèn)題:當(dāng)序列空間為R[0,1....n];時(shí),該怎么去使用堆排序呢?元素后移一位,這明顯不是一個(gè)好方法。
數(shù)據(jù)對(duì)齊,是指數(shù)據(jù)所在的內(nèi)存地址必須是該數(shù)據(jù)長(zhǎng)度的整數(shù)倍。比如DWORD數(shù)據(jù)的內(nèi)存其實(shí)地址能被4除盡,WORD數(shù)據(jù)的內(nèi)存地址能被2除盡。x86 CPU能直接訪問(wèn)對(duì)齊的數(shù)據(jù),當(dāng)它試圖訪問(wèn)一個(gè)未對(duì)齊的數(shù)據(jù)時(shí),會(huì)在內(nèi)部進(jìn)行一系列的調(diào)整,這些調(diào)整對(duì)于程序來(lái)說(shuō)是透明的,但是會(huì)降低運(yùn)行速度,所以編譯器在編譯程序時(shí)會(huì)盡量保持?jǐn)?shù)據(jù)對(duì)齊。
C/C++編譯器在內(nèi)存分配時(shí)也保持了數(shù)據(jù)對(duì)齊,請(qǐng)看下例:
struct{
short a1;
short a2;
short a3;
}A;
struct{
long a1;
short a2;
}B;
cout<<sizeof(A)<<","<<sizeof(B)<<endl;//其它代碼略去
結(jié)構(gòu)體A和B的大小分別是多少呢?
默認(rèn)情況下,為了方便對(duì)結(jié)構(gòu)體元素的訪問(wèn)和管理,當(dāng)結(jié)構(gòu)體內(nèi)的元素都小于處理器長(zhǎng)度的時(shí)候,便以結(jié)構(gòu)體里面最長(zhǎng)的數(shù)據(jù)為對(duì)齊單位,也就是說(shuō),結(jié)構(gòu)體的長(zhǎng)度一定是最長(zhǎng)數(shù)據(jù)長(zhǎng)度的整數(shù)倍。
如果結(jié)構(gòu)體內(nèi)部存在長(zhǎng)度大于處理器位數(shù)時(shí)就以處理器位數(shù)為對(duì)齊單位。
結(jié)構(gòu)體內(nèi)類型相同的連續(xù)元素將存在連續(xù)的空間內(nèi),和數(shù)組一樣。
上例中:
A有3個(gè)short類型變量,各自占2字節(jié),總和為6,6是2的倍數(shù),所以sizeof(A)=6;
B有一個(gè)long類型變量,占4字節(jié),一個(gè)short類型的變量,占2字節(jié),總和6不是最大長(zhǎng)度4的倍數(shù),所以要補(bǔ)空字節(jié)以增至8實(shí)現(xiàn)對(duì)齊,所以sizeof(8)=8。
在C++類的設(shè)計(jì)中遵循同樣的道理,但需注意,空類需要占1個(gè)字節(jié),靜態(tài)變量(static)由于在棧中分配,不在sizeof計(jì)算范圍內(nèi)。
多態(tài)性,這個(gè)面向?qū)ο缶幊填I(lǐng)域的核心概念,本身的內(nèi)容博大精深,要以一文說(shuō)清楚實(shí)在是不太可能。加之作者本人也還在不斷學(xué)習(xí)中,水平有限。因此本文只能描一下多態(tài)的輪廓,使讀者能夠了解個(gè)大概。如果有描的不準(zhǔn)的地方,歡迎指出,或與作者探討(作者Email:nicrosoft@sunistudio.com)
首先,什么是多態(tài)(Polymorphisn)?按字面的意思就是“多種形狀”。我手頭的書(shū)上沒(méi)有找到一個(gè)多態(tài)的理論性的概念的描述。暫且引用一下Charlie Calverts的對(duì)多態(tài)的描述吧——多態(tài)性是允許你將父對(duì)象設(shè)置成為和一個(gè)或更多的他的子對(duì)象相等的技術(shù),賦值之后,父對(duì)象就可以根據(jù)當(dāng)前賦值給它的子對(duì)象的特性以不同的方式運(yùn)作(摘自“Delphi4 編程技術(shù)內(nèi)幕”)。簡(jiǎn)單的說(shuō),就是一句話:允許將子類類型的指針賦值給父類類型的指針。多態(tài)性在Object Pascal和C++中都是通過(guò)虛函數(shù)(Virtual Function)實(shí)現(xiàn)的。
好,接著是“虛函數(shù)”(或者是“虛方法”)。虛函數(shù)就是允許被其子類重新定義的成員函數(shù)。而子類重新定義父類虛函數(shù)的做法,稱為“覆蓋”(override),或者稱為“重寫(xiě)”。
這里有一個(gè)初學(xué)者經(jīng)常混淆的概念。覆蓋(override)和重載(overload)。上面說(shuō)了,覆蓋是指子類重新定義父類的虛函數(shù)的做法。而重載,是指允許存在多個(gè)同名函數(shù),而這些函數(shù)的參數(shù)表不同(或許參數(shù)個(gè)數(shù)不同,或許參數(shù)類型不同,或許兩者都不同)。其實(shí),重載的概念并不屬于“面向?qū)ο缶幊?#8221;,重載的實(shí)現(xiàn)是:編譯器根據(jù)函數(shù)不同的參數(shù)表,對(duì)同名函數(shù)的名稱做修飾,然后這些同名函數(shù)就成了不同的函數(shù)(至少對(duì)于編譯器來(lái)說(shuō)是這樣的)。如,有兩個(gè)同名函數(shù):function func(p:integer):integer;和function func(p:string):integer;。那么編譯器做過(guò)修飾后的函數(shù)名稱可能是這樣的:int_func、str_func。對(duì)于這兩個(gè)函數(shù)的調(diào)用,在編譯器間就已經(jīng)確定了,是靜態(tài)的(記住:是靜態(tài))。也就是說(shuō),它們的地址在編譯期就綁定了(早綁定),因此,重載和多態(tài)無(wú)關(guān)!真正和多態(tài)相關(guān)的是“覆蓋”。當(dāng)子類重新定義了父類的虛函數(shù)后,父類指針根據(jù)賦給它的不同的子類指針,動(dòng)態(tài)(記住:是動(dòng)態(tài)!)的調(diào)用屬于子類的該函數(shù),這樣的函數(shù)調(diào)用在編譯期間是無(wú)法確定的(調(diào)用的子類的虛函數(shù)的地址無(wú)法給出)。因此,這樣的函數(shù)地址是在運(yùn)行期綁定的(晚邦定)。結(jié)論就是:重載只是一種語(yǔ)言特性,與多態(tài)無(wú)關(guān),與面向?qū)ο笠矡o(wú)關(guān)!
引用一句Bruce Eckel的話:“不要犯傻,如果它不是晚邦定,它就不是多態(tài)。”
那么,多態(tài)的作用是什么呢?我們知道,封裝可以隱藏實(shí)現(xiàn)細(xì)節(jié),使得代碼模塊化;繼承可以擴(kuò)展已存在的代碼模塊(類);它們的目的都是為了——代碼重用。而多態(tài)則是為了實(shí)現(xiàn)另一個(gè)目的——接口重用!而且現(xiàn)實(shí)往往是,要有效重用代碼很難,而真正最具有價(jià)值的重用是接口重用,因?yàn)?#8220;接口是公司最有價(jià)值的資源。設(shè)計(jì)接口比用一堆類來(lái)實(shí)現(xiàn)這個(gè)接口更費(fèi)時(shí)間。而且接口需要耗費(fèi)更昂貴的人力的時(shí)間。”
其實(shí),繼承的為重用代碼而存在的理由已經(jīng)越來(lái)越薄弱,因?yàn)?#8220;組合”可以很好的取代繼承的擴(kuò)展現(xiàn)有代碼的功能,而且“組合”的表現(xiàn)更好(至少可以防止“類爆炸”)。因此筆者個(gè)人認(rèn)為,繼承的存在很大程度上是作為“多態(tài)”的基礎(chǔ)而非擴(kuò)展現(xiàn)有代碼的方式了。
什么是接口重用?我們舉一個(gè)簡(jiǎn)單的例子,假設(shè)我們有一個(gè)描述飛機(jī)的基類(Object Pascal語(yǔ)言描述,下同):
type
plane = class
public
procedure fly(); virtual; abstract; //起飛純虛函數(shù)
procedure land(); virtual; abstract; //著陸純虛函數(shù)
function modal() : string; virtual; abstract; //查尋型號(hào)純虛函數(shù)
end;
然后,我們從plane派生出兩個(gè)子類,直升機(jī)(copter)和噴氣式飛機(jī)(jet):
copter = class(plane)
private
fModal : String;
public
constructor Create();
destructor Destroy(); override;
procedure fly(); override;
procedure land(); override;
function modal() : string; override;
end;
jet = class(plane)
private
fModal : String;
public
constructor Create();
destructor Destroy(); override;
procedure fly(); override;
procedure land(); override;
function modal() : string; override;
end;
現(xiàn)在,我們要完成一個(gè)飛機(jī)控制系統(tǒng),有一個(gè)全局的函數(shù) plane_fly,它負(fù)責(zé)讓傳遞給它的飛機(jī)起飛,那么,只需要這樣:
procedure plane_fly(const pplane : plane);
begin
pplane.fly();
end;
就可以讓所有傳給它的飛機(jī)(plane的子類對(duì)象)正常起飛!不管是直升機(jī)還是噴氣機(jī),甚至是現(xiàn)在還不存在的,以后會(huì)增加的飛碟。因?yàn)椋總€(gè)子類都已經(jīng)定義了自己的起飛方式。
可以看到 plane_fly函數(shù)接受參數(shù)的是 plane類對(duì)象引用,而實(shí)際傳遞給它的都是 plane的子類對(duì)象,現(xiàn)在回想一下開(kāi)頭所描述的“多態(tài)”:多態(tài)性是允許你將父對(duì)象設(shè)置成為和一個(gè)或更多的他的子對(duì)象相等的技術(shù),賦值之后,父對(duì)象就可以根據(jù)當(dāng)前賦值給它的子對(duì)象的特性以不同的方式運(yùn)作。
很顯然,parent = child; 就是多態(tài)的實(shí)質(zhì)!因?yàn)橹鄙龣C(jī)“是一種”飛機(jī),噴氣機(jī)也“是一種”飛機(jī),因此,所有對(duì)飛機(jī)的操作,都可以對(duì)它們操作,此時(shí),飛機(jī)類就作為一種接口。
多態(tài)的本質(zhì)就是將子類類型的指針賦值給父類類型的指針(在OP中是引用),只要這樣的賦值發(fā)生了,多態(tài)也就產(chǎn)生了,因?yàn)閷?shí)行了“向上映射”。
多態(tài)性
是允許將父對(duì)象設(shè)置成為和一個(gè)或多個(gè)它的子對(duì)象相等的技術(shù),比如Parent:=Child; 多態(tài)性使得能夠利用同一類(基類)類型的指針來(lái)引用不同類的對(duì)象,以及根據(jù)所引用對(duì)象的不同,以不同的方式執(zhí)行相同的操作.
c++中多態(tài)更容易理解的概念為
允許父類指針或名稱來(lái)引用子類對(duì)象,或?qū)ο蠓椒ǎ鴮?shí)際調(diào)用的方法為對(duì)象的類類型方法。
作用
把不同的子類對(duì)象都當(dāng)作父類來(lái)看,可以屏蔽不同子類對(duì)象之間的差異,寫(xiě)出通用的代碼,做出通用的編程,以適應(yīng)需求的不斷變化。
賦值之后,父對(duì)象就可以根據(jù)當(dāng)前賦值給它的子對(duì)象的特性以不同的方式運(yùn)作。也就是說(shuō),父親的行為像兒子,而不是兒子的行為像父親。
舉個(gè)例子:從一個(gè)基類中派生,響應(yīng)一個(gè)虛命令,產(chǎn)生不同的結(jié)果。
比如從某個(gè)基類繼承出多個(gè)對(duì)象,其基類有一個(gè)虛方法Tdoit,然后其子類也有這個(gè)方法,但行為不同,然后這些子對(duì)象中的任何一個(gè)可以賦給其基類的對(duì)象,這樣其基類的對(duì)象就可以執(zhí)行不同的操作了。實(shí)際上你是在通過(guò)其基類來(lái)訪問(wèn)其子對(duì)象的,你要做的就是一個(gè)賦值操作。
使用繼承性的結(jié)果就是可以創(chuàng)建一個(gè)類的家族,在認(rèn)識(shí)這個(gè)類的家族時(shí),就是把導(dǎo)出類的對(duì)象當(dāng)作基類的對(duì)象,這種認(rèn)識(shí)又叫作upcasting。這樣認(rèn)識(shí)的重要性在于:我們可以只針對(duì)基類寫(xiě)出一段程序,但它可以適應(yīng)于這個(gè)類的家族,因?yàn)?a target="_blank">編譯器會(huì)自動(dòng)就找出合適的對(duì)象來(lái)執(zhí)行操作。這種現(xiàn)象又稱為多態(tài)性。而實(shí)現(xiàn)多態(tài)性的手段又叫稱動(dòng)態(tài)綁定(dynamic binding)。
簡(jiǎn)單的說(shuō),建立一個(gè)父類的對(duì)象,它的內(nèi)容可以是這個(gè)父類的,也可以是它的子類的,當(dāng)子類擁有和父類同樣的函數(shù),當(dāng)使用這個(gè)對(duì)象調(diào)用這個(gè)函數(shù)的時(shí)候,定義這個(gè)對(duì)象的類(也就是父類)里的同名函數(shù)將被調(diào)用,當(dāng)在父類里的這個(gè)函數(shù)前加virtual關(guān)鍵字,那么子類的同名函數(shù)將被調(diào)用。
1、什么是虛函數(shù)?
①、虛函數(shù)必須是基類的非
靜態(tài)成員函數(shù)
②、其訪問(wèn)權(quán)限可以是protected或public。不能是private ,因?yàn)樽宇惱^承時(shí),子類不能訪問(wèn)。
③、在編譯時(shí)是動(dòng)態(tài)聯(lián)編的::編譯程序在編譯階段并不能確切知道將要調(diào)用的函數(shù),只有在
程序執(zhí)行時(shí)才能確定將要調(diào)用的函數(shù),為此要確切知道該調(diào)用的函數(shù),要求聯(lián)編工作要在程序運(yùn)行時(shí)進(jìn)行,這種在程序運(yùn)行時(shí)進(jìn)行聯(lián)編工作被稱為動(dòng)態(tài)聯(lián)編。
動(dòng)態(tài)聯(lián)編規(guī)定,只能通過(guò)指向基類的指針或基類對(duì)象的引用來(lái)調(diào)用虛函數(shù)2、定義形式。
virtual 函數(shù)返回值類型 虛函數(shù)名(形參表)
{ 函數(shù)體 }
純虛函數(shù):virtual 函數(shù)名=0
3、虛函數(shù)內(nèi)部機(jī)制。
①、每個(gè)實(shí)例對(duì)象里有自己的指針。
②、虛函數(shù)(Virtual Function)是通過(guò)一張?zhí)摵瘮?shù)表(Virtual Table)來(lái)實(shí)現(xiàn)的。
③、我們通過(guò)對(duì)象實(shí)例的地址得到這張?zhí)摵瘮?shù)表,然后就可以遍歷其中函數(shù)指針,并調(diào)用相應(yīng)的函數(shù)。
例子:
假設(shè)我們有這樣的一個(gè)類:
class Base {
public:
virtual void f() { cout << "Base::f" << endl; }
virtual void g() { cout << "Base::g" << endl; }
virtual void h() { cout << "Base::h" << endl; }
};
按照上面的說(shuō)法,我們可以通過(guò)Base的實(shí)例來(lái)得到虛函數(shù)表。 下面是實(shí)際例程:
typedef void(*Fun)(void);
Base b;
Fun pFun = NULL;
cout << "虛函數(shù)表地址:" << (int*)(&b) << endl;
cout << "虛函數(shù)表 — 第一個(gè)函數(shù)地址:" << (int*)*(int*)(&b) << endl;
/*這里的一點(diǎn)爭(zhēng)議的個(gè)人看法*/
原文認(rèn)為(int*)(&b)是虛表的地址,而很多網(wǎng)友都說(shuō),(包括我也認(rèn)為):(int *)*(int*)(&b)才是虛表地址
而(int*)*((int*)*(int*)(&b)); 才是虛表第一個(gè)虛函數(shù)的地址。
其實(shí)看后面的調(diào)用pFun = (Fun)*((int*)*(int*)(&b)); 就可以看出,*((int*)*(int*)(&b));轉(zhuǎn)成函數(shù)指針給pFun,然后正確的調(diào)用到了虛函數(shù)virtual void f()。
// Invoke the first virtual function
pFun = (Fun)*((int*)*(int*)(&b));
pFun();
實(shí)際運(yùn)行經(jīng)果如下:(Windows XP+VS2003, Linux 2.6.22 + GCC 4.1.3)
虛函數(shù)表地址:0012FED4
虛函數(shù)表 — 第一個(gè)函數(shù)地址:0044F148
Base::f
通過(guò)這個(gè)示例,我們可以看到,我們可以通過(guò)強(qiáng)行把&b轉(zhuǎn)成int *,取得虛函數(shù)表的地址,然后,再次取址就可以得到第一個(gè)虛函數(shù)的地址了,也就是Base::f(),這在上面的程序中得到了驗(yàn)證(把int* 強(qiáng)制轉(zhuǎn)成了函數(shù)指針)。通過(guò)這個(gè)示例,我們就可以知道如果要調(diào)用Base::g()和Base::h(),其代碼如下:
(Fun)*((int*)*(int*)(&b)+0); // Base::f()
(Fun)*((int*)*(int*)(&b)+1); // Base::g()
(Fun)*((int*)*(int*)(&b)+2); // Base::h()
這個(gè)時(shí)候你應(yīng)該懂了吧。什么?還是有點(diǎn)暈。也是,這樣的代碼看著太亂了。沒(méi)問(wèn)題,讓我畫(huà)個(gè)圖解釋一下。如下所示:
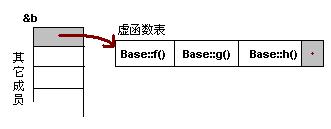
注意:在上面這個(gè)圖中,我在虛函數(shù)表的最后多加了一個(gè)結(jié)點(diǎn),這是虛函數(shù)表的結(jié)束結(jié)點(diǎn),就像字符串的結(jié)束符“\0”一樣,其標(biāo)志了虛函數(shù)表的結(jié)束。這個(gè)結(jié)束標(biāo)志的值在不同的編譯器下是不同的。在WinXP+VS2003下,這個(gè)值是NULL。而在Ubuntu 7.10 + Linux 2.6.22 + GCC 4.1.3下,這個(gè)值是如果1,表示還有下一個(gè)虛函數(shù)表,如果值是0,表示是最后一個(gè)虛函數(shù)表。
下面,我將分別說(shuō)明“無(wú)覆蓋”和“有覆蓋”時(shí)的虛函數(shù)表的樣子。沒(méi)有覆蓋父類的虛函數(shù)是毫無(wú)意義的。我之所以要講述沒(méi)有覆蓋的情況,主要目的是為了給一個(gè)對(duì)比。在比較之下,我們可以更加清楚地知道其內(nèi)部的具體實(shí)現(xiàn)。
一般繼承(無(wú)虛函數(shù)覆蓋)
下面,再讓我們來(lái)看看繼承時(shí)的虛函數(shù)表是什么樣的。假設(shè)有如下所示的一個(gè)繼承關(guān)系:
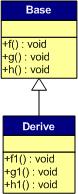
請(qǐng)注意,在這個(gè)繼承關(guān)系中,子類沒(méi)有重載任何父類的函數(shù)。那么,在派生類的實(shí)例中,其虛函數(shù)表如下所示:
對(duì)于實(shí)例:Derive d; 的虛函數(shù)表如下:
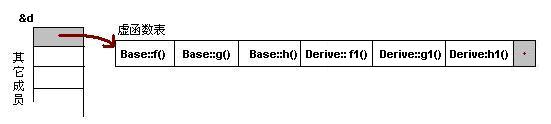
我們可以看到下面幾點(diǎn):
1)虛函數(shù)按照其聲明順序放于表中。
2)父類的虛函數(shù)在子類的虛函數(shù)前面。
我相信聰明的你一定可以參考前面的那個(gè)程序,來(lái)編寫(xiě)一段程序來(lái)驗(yàn)證。
一般繼承(有虛函數(shù)覆蓋)
覆蓋父類的虛函數(shù)是很顯然的事情,不然,虛函數(shù)就變得毫無(wú)意義。下面,我們來(lái)看一下,如果子類中有虛函數(shù)重載了父類的虛函數(shù),會(huì)是一個(gè)什么樣子?假設(shè),我們有下面這樣的一個(gè)繼承關(guān)系。
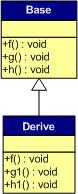
為了讓大家看到被繼承過(guò)后的效果,在這個(gè)類的設(shè)計(jì)中,我只覆蓋了父類的一個(gè)函數(shù):f()。那么,對(duì)于派生類的實(shí)例,其虛函數(shù)表會(huì)是下面的一個(gè)樣子:
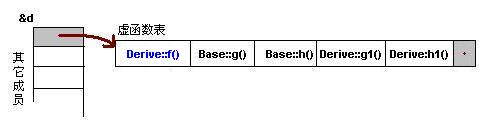
我們從表中可以看到下面幾點(diǎn),
1)覆蓋的f()函數(shù)被放到了虛表中原來(lái)父類虛函數(shù)的位置。
2)沒(méi)有被覆蓋的函數(shù)依舊。
這樣,我們就可以看到對(duì)于下面這樣的程序,
Base *b = new Derive();
b->f();
由b所指的內(nèi)存中的虛函數(shù)表的f()的位置已經(jīng)被Derive::f()函數(shù)地址所取代,于是在實(shí)際調(diào)用發(fā)生時(shí),是Derive::f()被調(diào)用了。這就實(shí)現(xiàn)了多態(tài)。
多重繼承(無(wú)虛函數(shù)覆蓋)
下面,再讓我們來(lái)看看多重繼承中的情況,假設(shè)有下面這樣一個(gè)類的繼承關(guān)系。注意:子類并沒(méi)有覆蓋父類的函數(shù)。
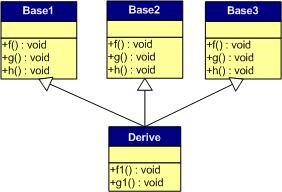
對(duì)于子類實(shí)例中的虛函數(shù)表,是下面這個(gè)樣子:
 我們可以看到:
我們可以看到:
1) 每個(gè)父類都有自己的虛表。
2) 子類的成員函數(shù)被放到了第一個(gè)父類的表中。(所謂的第一個(gè)父類是按照聲明順序來(lái)判斷的)
這樣做就是為了解決不同的父類類型的指針指向同一個(gè)子類實(shí)例,而能夠調(diào)用到實(shí)際的函數(shù)。
多重繼承(有虛函數(shù)覆蓋)
下面我們?cè)賮?lái)看看,如果發(fā)生虛函數(shù)覆蓋的情況。
下圖中,我們?cè)谧宇愔懈采w了父類的f()函數(shù):
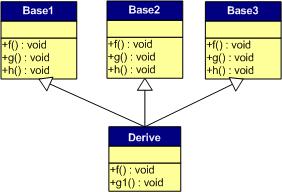
下面是對(duì)于子類實(shí)例中的虛函數(shù)表的圖:

我們可以看見(jiàn),三個(gè)父類虛函數(shù)表中的f()的位置被替換成了子類的函數(shù)指針。這樣,我們就可以任一靜態(tài)類型的父類來(lái)指向子類,并調(diào)用子類的f()了。如:
Derive d;
Base1 *b1 = &d;
Base2 *b2 = &d;
Base3 *b3 = &d;
b1->f(); //Derive::f()
b2->f(); //Derive::f()
b3->f(); //Derive::f()
b1->g(); //Base1::g()
b2->g(); //Base2::g()
b3->g(); //Base3::g()
安全性
每次寫(xiě)C++的文章,總免不了要批判一下C++。這篇文章也不例外。通過(guò)上面的講述,相信我們對(duì)虛函數(shù)表有一個(gè)比較細(xì)致的了解了。水可載舟,亦可覆舟。下面,讓我們來(lái)看看我們可以用虛函數(shù)表來(lái)干點(diǎn)什么壞事吧。
一、通過(guò)父類型的指針訪問(wèn)子類自己的虛函數(shù)
我們知道,子類沒(méi)有重載父類的虛函數(shù)是一件毫無(wú)意義的事情。因?yàn)槎鄳B(tài)也是要基于函數(shù)重載的。雖然在上面的圖中我們可以看到Base1的虛表中有Derive的虛函數(shù),但我們根本不可能使用下面的語(yǔ)句來(lái)調(diào)用子類的自有虛函數(shù):
Base1 *b1 = new Derive();
b1->f1(); //編譯出錯(cuò)
任何妄圖使用父類指針想調(diào)用子類中的未覆蓋父類的成員函數(shù)的行為都會(huì)被編譯器視為非法,所以,這樣的程序根本無(wú)法編譯通過(guò)。但在運(yùn)行時(shí),我們可以通過(guò)指針的方式訪問(wèn)虛函數(shù)表來(lái)達(dá)到違反C++語(yǔ)義的行為。(關(guān)于這方面的嘗試,通過(guò)閱讀后面附錄的代碼,相信你可以做到這一點(diǎn))
二、訪問(wèn)non-public的虛函數(shù)
另外,如果父類的虛函數(shù)是private或是protected的,但這些非public的虛函數(shù)同樣會(huì)存在于虛函數(shù)表中,所以,我們同樣可以使用訪問(wèn)虛函數(shù)表的方式來(lái)訪問(wèn)這些non-public的虛函數(shù),這是很容易做到的。
如:
class Base {
private:
virtual void f() { cout << "Base::f" << endl; }
};
class Derive : public Base{
};
typedef void(*Fun)(void);
void main() {
Derive d;
Fun pFun = (Fun)*((int*)*(int*)(&d)+0);
pFun();
}
結(jié)束語(yǔ)
C++這門(mén)語(yǔ)言是一門(mén)Magic的語(yǔ)言,對(duì)于程序員來(lái)說(shuō),我們似乎永遠(yuǎn)摸不清楚這門(mén)語(yǔ)言背著我們?cè)诟闪耸裁础P枰煜み@門(mén)語(yǔ)言,我們就必需要了解C++里面的那些東西,需要去了解C++中那些危險(xiǎn)的東西。不然,這是一種搬起石頭砸自己腳的編程語(yǔ)言。
本文來(lái)自CSDN博客,轉(zhuǎn)載請(qǐng)標(biāo)明出處:http://blog.csdn.net/hairetz/archive/2009/04/29/4137000.aspx
//轉(zhuǎn)自網(wǎng)友博客、
1、 派生類對(duì)象與普通類對(duì)象的相同之處在于,可以直接訪問(wèn)該類的所有對(duì)象(包括this指針指向的對(duì)象和其他對(duì)象)的protected和private成員(包括其基類成員)。不同之處在于派生類對(duì)象只能訪問(wèn)其對(duì)應(yīng)基類對(duì)象的protected成員(有隱式this指針傳遞),而不能訪問(wèn)其基類的其他對(duì)象的protect成員,而普通類對(duì)象則也可以直接訪問(wèn)該類所有對(duì)象的成員。
2、 在C++中,基類指針只能訪問(wèn)在該基類中被聲明(或繼承)的數(shù)據(jù)成員和成員函數(shù)(包括虛擬成員函數(shù)),而與它可能指向的實(shí)際對(duì)象無(wú)關(guān),所以如果需要用基類指針來(lái)訪問(wèn)一個(gè)沒(méi)有在該基類中聲明但是又在其派生類中定義了的成員,則需要執(zhí)行dynamic_cast來(lái)完成從基類指針到派生類指針的安全向下轉(zhuǎn)換。把一個(gè)成員聲明為虛擬的,只推延了“在程序執(zhí)行期間根據(jù)指針指向的實(shí)際類類型,對(duì)于要調(diào)用實(shí)例的解析過(guò)程”
3、 關(guān)于基類,派生類的相關(guān)補(bǔ)充:
1、 派生表中指定的類必須先被定義好,方可被指定為基類。
2、 派生類的前向聲明不能包括其派生表,而只需要類名即可。
3、 缺省的繼承是private。
4、 繼承而來(lái)的派生類的虛擬函數(shù)一般加上virtual較好,也可以省略。但基類中一定要聲明為virtual。
5、 對(duì)于基類的靜態(tài)成員,所有派生類對(duì)象都引用基類創(chuàng)建的這個(gè)相同,單一,共享的靜態(tài)成員,而不是創(chuàng)建該派生類的另一個(gè)獨(dú)立的靜態(tài)成員。
6、 友員關(guān)系不會(huì)被繼承,派生類沒(méi)有成為“向它的基類授權(quán)友誼的類”的友員。
4、 繼承機(jī)制下,派生類對(duì)象的構(gòu)造函數(shù)(析構(gòu)函數(shù))調(diào)用順序?yàn)椋?/div>
1、 基類(子對(duì)象的)構(gòu)造函數(shù),若有多個(gè)基類,則以類派生表中出現(xiàn)的順序?yàn)樾颉?/div>
2、 成員類對(duì)象的構(gòu)造函數(shù),若有多個(gè)成員類對(duì)象,則以它們?cè)陬惗x中被聲明的順序?yàn)樾颉?/div>
3、派生類自己的構(gòu)造函數(shù)。
4、派生類對(duì)象的析構(gòu)函數(shù)的調(diào)用順序與它的構(gòu)造函數(shù)相反。繼承機(jī)制下,析構(gòu)函數(shù)的行為如下:派生類的析構(gòu)函數(shù)先被調(diào)用,再靜態(tài)調(diào)用基類的析構(gòu)函數(shù)(從直接基類開(kāi)始)。注意一般基類的析構(gòu)函數(shù)不應(yīng)該是protected,因?yàn)樘摂M函數(shù)承接了“調(diào)用者所屬類類型的訪問(wèn)級(jí)別”。作為一般規(guī)則,我們建議將類層次結(jié)構(gòu)的根基類(聲明了一個(gè)或多個(gè)虛擬函數(shù))的析構(gòu)函數(shù)聲明為虛擬的。
5、 關(guān)于繼承機(jī)制下基類構(gòu)造函數(shù)(析構(gòu)函數(shù))相關(guān)的幾點(diǎn)說(shuō)明:
1、 作為一般規(guī)則,派生類構(gòu)造函數(shù)應(yīng)不能直接向一個(gè)基類的數(shù)據(jù)成員賦值,而是要把值傳遞給適當(dāng)?shù)幕悩?gòu)造函數(shù)來(lái)達(dá)到初始化賦值的目的。(一般是通過(guò)成員初始化表的方式)
2、 若基類不用于創(chuàng)建對(duì)象,則最好將其構(gòu)造函數(shù)放在protect區(qū),只允許其派生類對(duì)象調(diào)用;若基類只允許創(chuàng)建某一個(gè)特定的派生類類型的對(duì)象,則應(yīng)該將基類的構(gòu)造函數(shù)放在private區(qū),并將此特定的派生類聲明為該基類的友元來(lái)達(dá)到目的。
3、 派生類并不繼承基類的構(gòu)造函數(shù),每個(gè)派生類都必須提供自己的構(gòu)造函數(shù)集,派生類的構(gòu)造函數(shù)只能合法的調(diào)用其直接基類的構(gòu)造函數(shù)。(注意這里虛擬繼承提供了一個(gè)特例:虛擬基類的初始化變成了最終派生類的責(zé)任)。
6、 關(guān)于虛擬函數(shù)的相關(guān)
1、 必須使用指針或者引用來(lái)支持虛擬函數(shù)機(jī)制(面向?qū)ο蟪绦蛟O(shè)計(jì)),基類對(duì)象由于其靜態(tài)編譯,故不會(huì)保留派生類的類型身份。
2、 第一次引入虛擬函數(shù)的基類時(shí),必須在類體中將虛擬函數(shù)聲明為virtual,但若在該基類外部定義該虛擬函數(shù)時(shí)不能指定virtual。該基類的派生類中該虛擬函數(shù)virtual可加可不加,但從多重繼承考慮,最好加上。
3、 派生類改寫(xiě)的基類虛擬函數(shù),其原型必須與基類虛擬函數(shù)完全匹配(包括const和返回值),但返回值有個(gè)特例:派生類實(shí)例的返回值可以是基類實(shí)例返回類型的公有派生類類型。
4、 純虛擬函數(shù)(聲明后緊跟=0,函數(shù)定義可寫(xiě)可不寫(xiě))只是提供了一個(gè)可被其派生類改寫(xiě)的接口,其本身不能通過(guò)虛擬機(jī)制被調(diào)用,但可以靜態(tài)調(diào)用(寫(xiě)了函數(shù)定義的虛基類的純虛擬函數(shù))。一般來(lái)說(shuō),虛擬函數(shù)的靜態(tài)調(diào)用的目的是為了效率(避免動(dòng)態(tài)綁定)。
5、 包含(或繼承)了一個(gè)或多個(gè)純虛擬函數(shù)的類被編譯器識(shí)別為抽象基類,抽象基類不能用來(lái)創(chuàng)建獨(dú)立的類對(duì)象,只能作為子對(duì)象出現(xiàn)在后續(xù)的派生類中。
6、通過(guò)基類指針來(lái)調(diào)用的虛擬函數(shù)的真正實(shí)例是在運(yùn)行時(shí)刻確定的。但傳給虛擬函數(shù)的缺省實(shí)參是在編譯時(shí)刻根據(jù)被調(diào)用函數(shù)的對(duì)象的類型決定的(也即是若通過(guò)基類指針或引用調(diào)用派生類實(shí)例的虛擬函數(shù),則傳遞給它的缺省實(shí)參是由基類指定的)。
7、 虛擬繼承和多繼承相關(guān):
1、 虛擬繼承主要實(shí)為了解決繼承了多個(gè)基類實(shí)例,但是只需要一份單獨(dú)的共享實(shí)例的情況。
2、 非虛擬派生中,派生類只能顯式的初始化其直接基類(即派生類只能調(diào)用其直接基類的構(gòu)造函數(shù)),而在虛擬派生中,虛擬基類的初始化變成了最終派生類的責(zé)任,這個(gè)最終派生類是由每個(gè)特定的類對(duì)象聲明來(lái)決定的,其非虛擬基類的初始化同非虛擬派生一樣,只能由其直接派生類完成。(即中間派生類的對(duì)于虛擬基類構(gòu)造函數(shù)的調(diào)用被抑制)。
3、 虛擬繼承下構(gòu)造函數(shù)的調(diào)用順序按直接基類的聲明順序,對(duì)每個(gè)繼承子樹(shù)作深度優(yōu)先遍歷。第一步按此順序調(diào)用所有虛擬基類的構(gòu)造函數(shù);第二步按此順序調(diào)用非虛擬基類的構(gòu)造函數(shù)。析構(gòu)函數(shù)的調(diào)用順序與構(gòu)造函數(shù)相反。
4、 虛擬基類成員的可視性,對(duì)于虛擬基類成員的繼承比該成員后來(lái)重新定義的實(shí)例權(quán)值(優(yōu)先級(jí))小,故特化的派生類實(shí)例名覆蓋了共享的虛擬基類的實(shí)例名。而在非虛擬派生下的解析引用過(guò)程,每個(gè)繼承得到的實(shí)例都有相同的權(quán)值(優(yōu)先級(jí))。
5、 繼承下派生類的類域被嵌套在基類類域中,若一個(gè)名字在派生類域中沒(méi)有被解析出來(lái),則編譯器在外圍基類域中查找該名字定義。在多繼承下,名字解析查找過(guò)程為先是在本類類域中查找,再對(duì)繼承子樹(shù)中的所有基類同時(shí)查找,每個(gè)繼承得到的實(shí)例都有相同的權(quán)值(優(yōu)先級(jí))。若在兩個(gè)或多個(gè)基類子樹(shù)中都找到了該名字,則對(duì)其的使用是二義的。
摘要: 一、 什么是設(shè)計(jì)模式。
毫無(wú)疑問(wèn),設(shè)計(jì)模式是前人總結(jié)下來(lái),一些設(shè)計(jì)經(jīng)驗(yàn)經(jīng)過(guò)被反復(fù)使用、并為多數(shù)人知曉、經(jīng)過(guò)分類編目。模式是一種問(wèn)題的解決思路,它已經(jīng)適用于一個(gè)實(shí)踐環(huán)境,并且可以適用于其他壞境。
最終由GoF總結(jié)出23種設(shè)計(jì)模式。
二、 為什么要使用。
根本原因是為了代碼復(fù)...
閱讀全文
摘要: 1、什么是Bridge模式?這個(gè)問(wèn)題我用一言兩語(yǔ)實(shí)在無(wú)法概括其根本。不過(guò)我是這樣分析的:①、對(duì)象這個(gè)概念可以認(rèn)為是由“屬性”和“行為”兩個(gè)部分組成的。屬性我們可以認(rèn)為是一種靜止的,是一種抽象;一般情況下,行為是包含在一個(gè)對(duì)象中,但是,在有的情況下,我們需要將這些行為也進(jìn)行歸類,形成一個(gè)總的行為接口,這就是橋模式的用處。②、Br...
閱讀全文
久久综合香蕉国产蜜臀AV|
老男人久久青草av高清|
99久久精品国产免看国产一区|
亚洲精品无码专区久久久|
久久精品无码午夜福利理论片|
久久精品九九亚洲精品天堂|
久久精品成人|
精品久久久久久综合日本|
日韩欧美亚洲国产精品字幕久久久|
久久人妻无码中文字幕|
色综合久久久久|
一本色道久久88—综合亚洲精品|
国产精品久久久久久影院|
久久久久99这里有精品10|
亚洲综合婷婷久久|
久久婷婷成人综合色综合|
中文字幕久久精品
|
久久久无码精品亚洲日韩软件|
久久久久高潮综合影院|
久久AⅤ人妻少妇嫩草影院|
久久99国产综合精品免费|
久久精品国产99国产精品亚洲
|
久久国产香蕉一区精品|
色综合久久综精品|
99久久久国产精品免费无卡顿|
av色综合久久天堂av色综合在
|
久久精品水蜜桃av综合天堂|
无码任你躁久久久久久老妇|
国产免费久久精品丫丫|
99热热久久这里只有精品68|
AV狠狠色丁香婷婷综合久久|
色综合久久久久久久久五月|
99蜜桃臀久久久欧美精品网站
|
蜜臀久久99精品久久久久久小说|
亚洲国产成人久久综合碰|
日批日出水久久亚洲精品tv|
一级做a爰片久久毛片看看|
午夜精品久久久久久影视riav|
亚洲国产精品嫩草影院久久|
一本色道久久综合狠狠躁篇
|
欧美大香线蕉线伊人久久|