原作:e-maxx(Russia) 發(fā)表于 2011.8.25
翻譯:vici
對容斥原理的描述
容斥原理是一種重要的組合數(shù)學(xué)方法,可以讓你求解任意大小的集合,或者計算復(fù)合事件的概率。
描述
容斥原理可以描述如下:
要計算幾個集合并集的大小,我們要先將所有單個集合的大小計算出來,然后減去所有兩個集合相交的部分,再加回所有三個集合相交的部分,再減去所有四個集合相交的部分,依此類推,一直計算到所有集合相交的部分。
關(guān)于集合的原理公式
上述描述的公式形式可以表示如下:
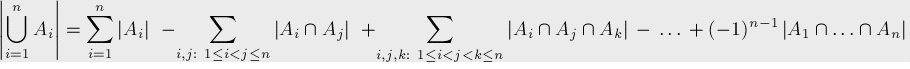
它可以寫得更簡潔一些,我們將B作為所有Ai的集合,那么容斥原理就變成了:
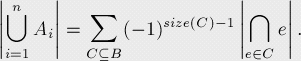
這個公式是由 De Moivre (Abraham de Moivre)提出的。
關(guān)于維恩圖的原理
用維恩圖來表示集合A、B和C:
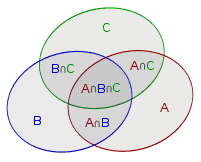
那么 的面積就是集合A、B、C各自面積之和減去
的面積就是集合A、B、C各自面積之和減去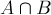 ,
, 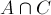 ,
, 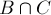 的面積,再加上
的面積,再加上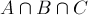 的面積。
的面積。
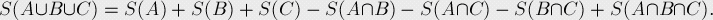
由此,我們也可以解決n個集合求并的問題。
關(guān)于概率論的原理
設(shè)事件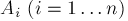 ,
,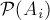 代表發(fā)生某些事件的概率(即發(fā)生其中至少一個事件的概率),則:
代表發(fā)生某些事件的概率(即發(fā)生其中至少一個事件的概率),則:
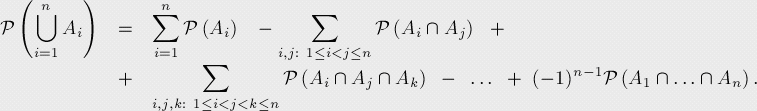
這個公式也可以用B代表Ai的集合:
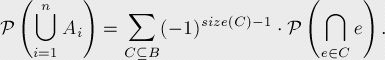
容斥原理的證明
我們要證明下面的等式:
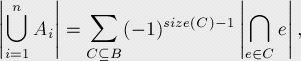
其中B代表全部Ai的集合
我們需要證明在Ai集合中的任意元素,都由右邊的算式被正好加上了一次(注意如果是不在Ai集合中的元素,是不會出現(xiàn)在右邊的算式中的)。
假設(shè)有一任意元素在k個Ai集合中(k>=1),我們來驗證這個元素正好被加了一次:
當(dāng)size(C)=1時,元素x被加了k次。
當(dāng)size(C)=2時,元素x被減了C(2,k)次,因為在k個集合中選擇2個,其中都包含x。
當(dāng)size(C)=3時,元素x被加了C(3,k)次。
……
當(dāng)size(C)=k時,元素x被加/減了C(k,k)次,符號由sign(-1)^(k-1)決定。
當(dāng)size(C)>k時,元素x不被考慮。
然后我們來計算所有組合數(shù)的和。
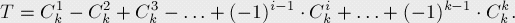
由二項式定理,我們可以將它變成:
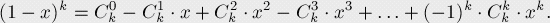
我們把x取為1,這時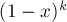 表示1-T(其中T為x被加的總次數(shù)),所以
表示1-T(其中T為x被加的總次數(shù)),所以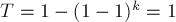 ,證明完畢。
,證明完畢。
對于實際問題的應(yīng)用
容斥原理的理論需要通過例子才能很好的理解。
首先,我們用三個簡單的例子來闡釋這個理論。然后會討論一些復(fù)雜問題,試看如何用容斥原理來解決它們。
其中的“尋找路徑數(shù)”是一個特殊的例子,它反映了容斥問題有時可以在多項式級復(fù)雜度內(nèi)解決,不一定需要指數(shù)級。
一個簡單的排列問題
由0到9的數(shù)字組成排列,要求第一個數(shù)大于1,最后一個數(shù)小于8,一共有多少種排列?
我們可以來計算它的逆問題,即第一個元素<=1或者最后一個元素>=8的情況。
我們設(shè)第一個元素<=1時有X組排列,最后一個元素>=8時有Y組排列。那么通過容斥原理來解決就可以寫成:
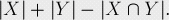
經(jīng)過簡單的組合運算,我們得到了結(jié)果:
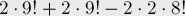
然后被總的排列數(shù)10!減,就是最終的答案了。
(0,1,2)序列問題
長度為n的由數(shù)字0,1,2組成的序列,要求每個數(shù)字至少出現(xiàn)1次,這樣的序列有多少種?
同樣的,我們轉(zhuǎn)向它的逆問題。也就是不出現(xiàn)這些數(shù)字的序列 不出現(xiàn)其中某些數(shù)字的序列。
我們定義Ai(i=0…2)表示不出現(xiàn)數(shù)字i的序列數(shù),那么由容斥原理,我們得到該逆問題的結(jié)果為:
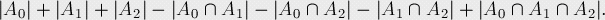
可以發(fā)現(xiàn)每個Ai的值都為2^n(因為這些序列中只能包含兩種數(shù)字)。而所有的兩兩組合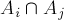 都為1(它們只包含1種數(shù)字)。最后,三個集合的交集為0。(因為它不包含數(shù)字,所以不存在)
都為1(它們只包含1種數(shù)字)。最后,三個集合的交集為0。(因為它不包含數(shù)字,所以不存在)
要記得我們解決的是它的逆問題,所以要用總數(shù)減掉,得到最終結(jié)果:
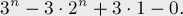
方程整數(shù)解問題
給出一個方程:
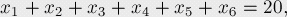
其中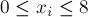 。
。
求這個方程的整數(shù)解有多少組。
我們先不去理會xi<=8的條件,來考慮所有正整數(shù)解的情況。這個很容易用組合數(shù)來求解,我們要把20個元素分成6組,也就是添加5塊“夾板”,然后在25個位置中找5塊“夾板”的位置。
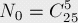
然后通過容斥原理來討論它的逆問題,也就是x>=9時的解。
我們定義Ak為xk>=9并且其他xi>=0時的集合,同樣我們用上面的添加“夾板”法來計算Ak的大小,因為有9個位置已經(jīng)被xk所利用了,所以:
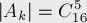
然后計算兩個這樣的集合Ak、Ap的交集:
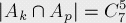
因為所有x的和不能超過20,所以三個或三個以上這樣的集合時是不能同時出現(xiàn)的,它們的交集都為0。最后我們用總數(shù)剪掉用容斥原理所求逆問題的答案,就得到了最終結(jié)果:
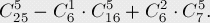
求指定區(qū)間內(nèi)與n互素的數(shù)的個數(shù):
給出整數(shù)n和r。求區(qū)間[1;r]中與n互素的數(shù)的個數(shù)。
去解決它的逆問題,求不與n互素的數(shù)的個數(shù)。
考慮n的所有素因子pi(i=1…k)
在[1;r]中有多少數(shù)能被pi整除呢?它就是:
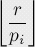
然而,如果我們單純將所有結(jié)果相加,會得到錯誤答案。有些數(shù)可能被統(tǒng)計多次(被好幾個素因子整除)。所以,我們要運用容斥原理來解決。
我們可以用2^k的算法求出所有的pi組合,然后計算每種組合的pi乘積,通過容斥原理來對結(jié)果進行加減處理。
關(guān)于此問題的最終實現(xiàn):
int solve (int n, int r) {
vector<int> p;
for (int i=2; i*i<=n; ++i)
if (n % i == 0) {
p.push_back (i);
while (n % i == 0)
n /= i;
}
if (n > 1)
p.push_back (n);
int sum = 0;
for (int msk=1; msk<(1<<p.size()); ++msk) {
int mult = 1,
bits = 0;
for (int i=0; i<(int)p.size(); ++i)
if (msk & (1<<i)) {
++bits;
mult *= p[i];
}
int cur = r / mult;
if (bits % 2 == 1)
sum += cur;
else
sum -= cur;
}
return r - sum;
}
算法的復(fù)雜度為 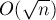 。
。
求在給定區(qū)間內(nèi),能被給定集合至少一個數(shù)整除的數(shù)個數(shù)
給出n個整數(shù)ai和整數(shù)r。求在區(qū)間[1;r]中,至少能被一個ai整除的數(shù)有多少。
解決此題的思路和上題差不多,計算ai所能組成的各種集合(這里將集合中ai的最小公倍數(shù)作為除數(shù))在區(qū)間中滿足的數(shù)的個數(shù),然后利用容斥原理實現(xiàn)加減。
此題中實現(xiàn)所有集合的枚舉,需要2^n的復(fù)雜度,求解lcm需要O(nlogr)的復(fù)雜度。
能滿足一定數(shù)目匹配的字符串的個數(shù)問題
給出n個匹配串,它們長度相同,其中有一些’?’表示待匹配的字母。然后給出一個整數(shù)k,求能正好匹配k個匹配串的字符串的個數(shù)。更進一步,求至少匹配k個匹配串的字符串的個數(shù)。
首先我們會發(fā)現(xiàn),我們很容易找到能匹配所有匹配串的字符串。只需要對比所有匹配串,去在每一列中找出現(xiàn)的字母(或者這一列全是’?’,或者這一列出現(xiàn)了唯一的字母,否則這樣的字符串就存在),最后所有字母組成的單詞即為所求。
現(xiàn)在我們來學(xué)習(xí)如何解決第一個問題:能正好匹配k個匹配串的字符串。
我們在n個匹配串中選出k個,作為集合X,統(tǒng)計滿足集合X中匹配的字符串?dāng)?shù)。求解這個問題時應(yīng)用容斥原理,對X的所有超集進行運算,得到每個X集合的結(jié)果:
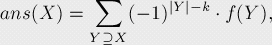
此處f(Y)代表滿足匹配集合Y的字符串?dāng)?shù)。
如果我們將所有的ans(X)相加,就可以得到最終結(jié)果:
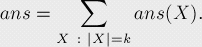
這樣,就得到了一個復(fù)雜度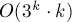 的解法。
的解法。
這個算法可以作一些改進,因為在求解ans(X)時有些Y集合是重復(fù)的。
回到利用容斥原理公式可以發(fā)現(xiàn),當(dāng)選定一個Y時,所有 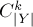 中X的結(jié)果都是相同的,其符號都為
中X的結(jié)果都是相同的,其符號都為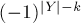 。所以可以用如下公式求解:
。所以可以用如下公式求解:
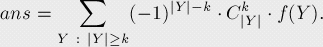
這樣就得到了一個復(fù)雜度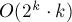 的解法。
的解法。
現(xiàn)在我們來求解第二個問題:能滿足至少k個匹配的字符串有多少個。
顯然的,我們可以用問題一的方法來計算滿足k到n的所有結(jié)果。問題一的結(jié)論依然成立,不同之處在于這個問題中的X不是大小都為k的,而是>=k的所有集合。
如此進行計算,最后將f(Y)作為另一個因子:將所有的ans做和,有點類似二項式展開:
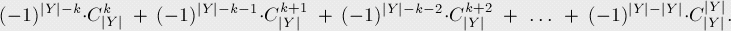
在《具體數(shù)學(xué)》( Graham, Knuth, Patashnik. "Concrete Mathematics" [1998] )中,介紹了一個著名的關(guān)于二項式系數(shù)的公式:
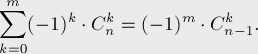
根據(jù)這個公式,可以將前面的結(jié)果進行化簡:
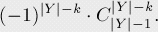
那么,對于這個問題,我們也得到了一個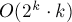 的解法:
的解法:
路徑的數(shù)目問題
在一個的 方格陣中,有k個格子是不可穿越的墻。一開始在格子(1,1)(最左下角的格子)中有一個機器人。這個機器人只能向上或向右行進,最后它將到達位于格子(n,m)的籠子里,其間不能經(jīng)過障礙物格子。求一共有多少種路線可以到達終點。
方格陣中,有k個格子是不可穿越的墻。一開始在格子(1,1)(最左下角的格子)中有一個機器人。這個機器人只能向上或向右行進,最后它將到達位于格子(n,m)的籠子里,其間不能經(jīng)過障礙物格子。求一共有多少種路線可以到達終點。
為了方便區(qū)分所有障礙物格子,我們建立坐標(biāo)系,用(x,y)表示格子的坐標(biāo)。
首先我們考慮沒有障礙物的時候:也就是如何求從一個點到另一個點的路徑數(shù)。如果從一個點在一個方向要走x個格子,在另一個方向要走y個格子,那么通過簡單的組合原理可以得知結(jié)果為:
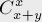
現(xiàn)在來考慮有障礙物時的情況,我們可以利用容斥原理:求出至少經(jīng)過一個障礙物時的路徑數(shù)。
對于這個例子,你可以枚舉所有障礙物的子集,作為需要要經(jīng)過的,計算經(jīng)過該集合障礙物的路徑數(shù)(求從原點到第一個障礙物的路徑數(shù)、第一個障礙物到第二個障礙物的路徑數(shù)…最后對這些路徑數(shù)求乘積),然后通過容斥原理,對這些結(jié)果作加法或減法。
然而,它是一個非多項式的解法,復(fù)雜度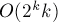 。下面我們將介紹一個多項式的解法。
。下面我們將介紹一個多項式的解法。
我們運用動態(tài)規(guī)劃:令d[i][j]代表從第i個點到第j個點,不經(jīng)過任何障礙物時的路徑數(shù)(當(dāng)然除了i和j)。那么我們總共需要k+2個點,包括k個障礙物點以及起點和終點。
首先我們算出從i點到j點的所有路徑數(shù),然后減掉經(jīng)過障礙物的那些“壞”的路線。讓我們看看如何計算“壞”的路線:枚舉i和j之間的所有障礙物點i<l<j,那么從i到j的“壞”路徑數(shù)就是所有d[i][l]和d[l][j]的乘積最后求和。再被總路徑數(shù)減掉就是d[i][j]的結(jié)果。
我們已經(jīng)知道計算總路徑數(shù)的復(fù)雜度為 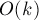 ,那么該解法的總復(fù)雜度為
,那么該解法的總復(fù)雜度為 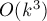 。
。
(譯注:這段算法有問題,事實上可以用O(k^2)方法解決)
素數(shù)四元組的個數(shù)問題
給出n個數(shù)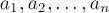 ,從其中選出4個數(shù),使它們的最大公約數(shù)為1,問總共有多少中取法。
,從其中選出4個數(shù),使它們的最大公約數(shù)為1,問總共有多少中取法。
我們解決它的逆問題:求最大公約數(shù)d>1的四元組的個數(shù)。
運用容斥原理,將求得的對于每個d的四元組個數(shù)的結(jié)果進行加減。
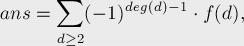
其中deg(d)代表d的質(zhì)因子個數(shù),f(d)代表四個數(shù)都能被d整除的四元組的個數(shù)。
求解f(d)時,只需要利用組合方法,求從所有滿足被d整除的ai中選4個的方法數(shù)。
然后利用容斥原理,統(tǒng)計出所有能被一個素數(shù)整除的四元組個數(shù),然后減掉所有能被兩個素數(shù)整除的四元組個數(shù),再加上被三個素數(shù)整除的四元組個數(shù)…
和睦數(shù)三元組的個數(shù)問題
給出一個整數(shù)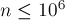 。選出a, b, c (其中2<=a<b<c<=n),組成和睦三元組,即:
。選出a, b, c (其中2<=a<b<c<=n),組成和睦三元組,即:
· 或者滿足 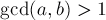 ,
, 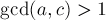 ,
, 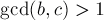
· 或者滿足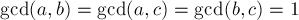
首先,我們考慮它的逆問題:也就是不和睦三元組的個數(shù)。
然后,我們可以發(fā)現(xiàn),在每個不和睦三元組的三個元素中,我們都能找到正好兩個元素滿足:它與一個元素互素,并且與另一個元素不互素。
所以,我們只需枚舉2到n的所有數(shù),將每個數(shù)的與其互素的數(shù)的個數(shù)和與其不互素的數(shù)的個數(shù)相乘,最后求和并除以2,就是要求的逆問題的答案。
現(xiàn)在我們要考慮這個問題,如何求與2到n這些數(shù)互素(不互素)的數(shù)的個數(shù)。雖然求解與一個數(shù)互素數(shù)的個數(shù)的解法在前面已經(jīng)提到過了,但在此并不合適,因為現(xiàn)在要求2到n所有數(shù)的結(jié)果,分別求解顯然效率太低。
所以,我們需要一個更快的算法,可以一次算出2到n所有數(shù)的結(jié)果。
在這里,我們可以使用改進的埃拉托色尼篩法。
· 首先,對于2到n的所有數(shù),我們要知道構(gòu)成它的素數(shù)中是否有次數(shù)大于1的,為了應(yīng)用容斥原理,我們還有知道它們由多少種不同的素數(shù)構(gòu)成。
對于這個問題,我們定義數(shù)組deg[i]:表示i由多少種不同素數(shù)構(gòu)成,以及good[i]:取值true或false,表示i包含素數(shù)的次數(shù)小于等于1是否成立。
再利用埃拉托色尼篩法,在遍歷到某個素數(shù)i時,枚舉它在2到n范圍內(nèi)的所有倍數(shù),更新這些倍數(shù)的deg[]值,如果有倍數(shù)包含了多個i,那么就把這個倍數(shù)的good[]值賦為false。
· 然后,利用容斥原理,求出2到n每個數(shù)的cnt[i]:在2到n中不與i互素的數(shù)的個數(shù)。
回想容斥原理的公式,它所求的集合是不會包含重復(fù)元素的。也就是如果這個集合包含的某個素數(shù)多于一次,它們不應(yīng)再被考慮。
所以只有當(dāng)一個數(shù)i滿足good[i]=true時,它才會被用于容斥原理。枚舉i的所有倍數(shù)i*j,那么對于i*j,就有N/i個與i*j同樣包含i(素數(shù)集合)的數(shù)。將這些結(jié)果進行加減,符號由deg[i](素數(shù)集合的大小)決定。如果deg[i]為奇數(shù),那么我們要用加號,否則用減號。
程序?qū)崿F(xiàn):
int n;
bool good[MAXN];
int deg[MAXN], cnt[MAXN];
long long solve() {
memset (good, 1, sizeof good);
memset (deg, 0, sizeof deg);
memset (cnt, 0, sizeof cnt);
long long ans_bad = 0;
for (int i=2; i<=n; ++i) {
if (good[i]) {
if (deg[i] == 0) deg[i] = 1;
for (int j=1; i*j<=n; ++j) {
if (j > 1 && deg[i] == 1)
if (j % i == 0)
good[i*j] = false;
else
++deg[i*j];
cnt[i*j] += (n / i) * (deg[i]%2==1 ? +1 : -1);
}
}
ans_bad += (cnt[i] - 1) * 1ll * (n - cnt[i] - 1);
}
return (n-1) * 1ll * (n-2) * (n-3) / 6 - ans_bad / 2;
}
最終算法的復(fù)雜度為 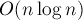 ,因為對于大部分i都要進行n/i次枚舉。
,因為對于大部分i都要進行n/i次枚舉。
錯排問題
我們想要證明如下的求解長度為n序列的錯排數(shù)的公式:
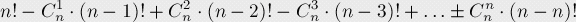
它的近似結(jié)果為:
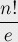
(此外,如果將這個近似式的結(jié)果向其最近的整數(shù)舍入,你就可以得到準(zhǔn)確結(jié)果)
我們定義Ak:在長度為n的序列中,有一個不動點位置為k(1<=k<=n)時的序列集合。
現(xiàn)在我們運用容斥原理來計算至少包含有一個不動點的排列數(shù),要計算這個,我們必須先算出所有Ak、以及它們的交集的排列數(shù)。
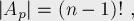
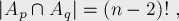
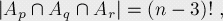
因為我們知道當(dāng)有x個不動點時,所有不動點的位置是固定的,而其它點可以任意排列。
用容斥原理對結(jié)果進行帶入,而從n個點中選x個不動點的組合數(shù)為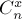 ,那么至少包含一個不動點的排列數(shù)為:
,那么至少包含一個不動點的排列數(shù)為:
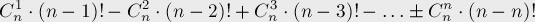
那么不包含不動點(即錯排數(shù))的結(jié)果就是:
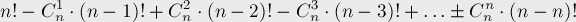
化簡這個式子,我們得到了錯排數(shù)的準(zhǔn)確式和近似式:
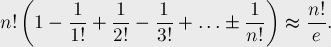
(因為括號中是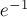 的泰勒展開式的前n+1項)
的泰勒展開式的前n+1項)
用這個式子也可以解決一些類似的問題,如果現(xiàn)在求有m個不動點的排列數(shù),那么我們可以對上式進行修改,也就是將括號中的累加到1/n!改成累加到1/(n-m)!。
在OJ的相關(guān)題目
這里列出了一些可以用容斥原理解決的習(xí)題。
· UVA #10325 "The Lottery" [難度:簡單]
· UVA #11806 "Cheerleaders" [難度:簡單]
· TopCoder SRM 477 "CarelessSecretary" [難度:簡單]
· TopCoder TCHS 16 "Divisibility" [難度:簡單]
· SPOJ #6285 NGM2 "Another Game With Numbers" [難度:簡單]
· TopCoder SRM 382 "CharmingTicketsEasy" [難度:中等]
· TopCoder SRM 390 "SetOfPatterns" [難度:中等]
· TopCoder SRM 176 "Deranged" [難度:中等]
· TopCoder SRM 457 "TheHexagonsDivOne" [難度:中等]
· SPOJ #4191 MSKYCODE "Sky Code" [難度:中等]
· SPOJ #4168 SQFREE "Square-free integers" [難度:中等]
· CodeChef "Count Relations" [難度:中等]
參考文獻
Debra K. Borkovitz.