是個(gè)經(jīng)典問(wèn)題了，求滿足a ^ 2 + b ^ 2 = c ^ 2且a、b、c兩兩互質(zhì)的三元組個(gè)數(shù)，其中a、b、c都小于等于n，同時(shí)還要求出n以內(nèi)不屬于三元組（不必互質(zhì)）的數(shù)的個(gè)數(shù)，其中n <= 1000000。
　　數(shù)據(jù)范圍很大，單純的n ^ 2的枚舉肯定是不行的。我發(fā)現(xiàn)互質(zhì)的三元組不多，想找一個(gè)辦法求出互質(zhì)的，然后篩出其他的三元組（乘以倍數(shù)），但是仍然想不出怎樣很快找到互質(zhì)的三元組。到網(wǎng)上查了一下，找到了一個(gè)很好的網(wǎng)站（http://xserve.math.nctu.edu.tw/people/cpai/carnival/fraction/05.htm）講解這個(gè)問(wèn)題。
　　首先只需找到互質(zhì)的a和b就可以了，其余的可以通過(guò)乘以一定的倍數(shù)得到。首先a和b必須不能都是奇數(shù)，否則的話，不妨設(shè)a = 2p + 1, b = 2q + 1, c = 2r。帶入a ^ 2 + b ^ 2 = c ^ 2有：2 * (r ^ 2 - p ^ 2 - q ^ 2 - p - q) = 1，出現(xiàn)了矛盾。這樣必然a和b一奇一偶，設(shè)a是偶數(shù)。恒等變換一下：（這里是x ^ 2 + y ^ 2 = z ^ 2，x是偶數(shù)）

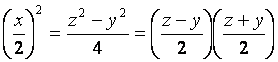
　　令u = (z - y) / 2，v = (z + y) / 2。因?yàn)閥、z互質(zhì)，那么u、v互質(zhì)。如果不互質(zhì)，有v = ku，變換后得到：z / y = (k + 1) / (k - 1)。因?yàn)閦和y互質(zhì)，這樣這個(gè)等式的解只能是z = k + 1且y = k - 1。這樣的話u = 1。可以理解為這也是互質(zhì)的特殊情況(gcd = 1)。這樣(x / 2) ^ 2 = u * v，u和v沒(méi)有公共的質(zhì)因數(shù)，因此必然u和v都是完全平方數(shù)。接下來(lái)的事情就比較簡(jiǎn)單了，令u = m ^ 2，v = n ^ 2，然后利用m和n表示x、y、z有：y = n ^ 2 - m ^ 2，x = 2 * m * n，z = n ^ 2 + m ^ 2。這樣題目中數(shù)據(jù)范圍1000000，而枚舉m和n的范圍最大1000，這個(gè)復(fù)雜度就可以接受了。枚舉的時(shí)候不用擔(dān)心出現(xiàn)重復(fù)的互質(zhì)的x與y，因?yàn)檫@里x一定是偶數(shù)，如果x和y已經(jīng)互質(zhì)，那么y一定是奇數(shù)，解是唯一的。
　　很囧的是這個(gè)巧妙的方法居然公元前250年就有大牛想到了（丟番圖），實(shí)在orz！