ŃĆĆŃĆĆÕģłÕüćĶ«Ša2 = t, ķóśńø«ŠlÖÕ«Üõ║åķĆƵĩÕģ│ń│╗ÕQÜAn = 2 * t * An-1 - An-2 (n > 2)ÕQīÕłØÕĆ╝A1 = 1, A2 = tÕQøķóśńø«Ķ”üµ▒éSn = An ^ 2 + An-1 ^ 2 + ... + A1 ^ 2ŃĆ?br>ŃĆĆŃĆĆÕÅŹÕżŹÕ║öńö©ķĆƵĩÕģ│ń│╗ÕŠŚÕł░ÕQ?br>ŃĆĆŃĆĆ
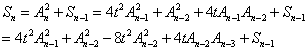
ŃĆĆŃĆĆńäČÕÉÄSn-1Õł®ńö©ńøĖÕÉīńÜäµ¢╣Õ╝ÅÕ▒ĢÕ╝ĆÕQīµŖŖ4tAn-2An-3ŠU”ÕÄ╗ÕQīÕŠŚÕłÄ═╝Ü
ŃĆĆŃĆĆ
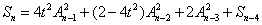
ŃĆĆŃĆĆśqÖµĀĘ׫▒µ»öĶŠāÕ«╣µśōÕŠŚÕć║SnńÜäķĆÜķĪ╣ÕQ?br>ŃĆĆŃĆĆ
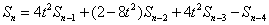
ŃĆĆŃĆĆÕĮōÕłØśqÖõĖ¬ķóśńø«õ╣ŗµēĆõ╗źµ▓Īµāø_ł░śqÖń¦Źµ¢ęÄ│ĢÕQīÕ░▒µś»ÕøĀõĖ▐ZĖĆń£ŗÕł░ķĆƵĩÕģ│ń│╗ÕQīÕ░▒µā│ńØĆńö©õĖĆĶł¼Ķ¦Żµ¢╣ń©ŗńÜäµ¢╣µ│ĢÕÄ╗µ▒éĶ¦ŻķĆÜķĪ╣ÕQīµĆØń╗┤Ķó½Õ▒ĆķÖÉõ║åÕQīÕģČÕ«×ńö©ĮÄĆÕŹĢńÜäµ¢╣Õ╝Å׫▒ÕÅ»õ╗źµÄ©Õć║µØźńÜäŃĆéõ╗źÕÉÄÕ»╣õ║ÄõĖĆõĖ¬ķŚ«ķóś’╝īÕ║öĶ»źõ╗ÄÕżÜõĖ¬µ¢╣ķØóÕÄ╗µā╗I╝īõĖŹĶāĮµāø_ĮōńäČÕĢŖŃĆéµā│ĶĄõh£Ćśqæń£ŗÕł░ńÜäõĖĆīDĄĶ»ØÕQīõ╗źµŁżĶć¬Õŗē’╝Ü
ŃĆĆŃĆƵŁŻÕłÖĶĪ©ĶŠŠÕ╝ÅķØ×ÕĖĖÕ╝║Õż¦’╝īõĮåµś»Õ«āÕŲłõĖŹĶāĮõĖ║µ»ÅõĖĆõĖ¬ķŚ«ķóśµÅÉõŠøµŁŻ╝ŗ«ńÜäĶ¦ŻÕå│µ¢ęÄĪłŃĆéõĮĀÕ║öĶ»źÕŁ”õ╣ĀŁæø_ż¤ÕżÜńÜäń¤źĶ»åÕQīõ╗źĶŠ©Õł½õ╗Ćõ╣łµŚČÕĆÖÕ«āõ╗¼µś»ÕÉłķĆéńÜäÕQīõ╗Ćõ╣łµŚČÕĆÖÕ«āõ╗¼õ╝ÜĶ¦ŻÕå│õĮĀńÜäķŚ«ķóśÕQīõ╗Ćõ╣łµŚČÕĆÖÕ«āõ╗¼õ±öńö¤ńÜäķŚ«ķóśµ»öĶ”üĶ¦ŻÕå│ńÜäķŚ«ķóśĶ┐śĶ”üÕżÜŃĆ?br>ŃĆĆŃĆĆõĖĆõ║øõØhÕQīķüćÕłŅCĖĆõĖ¬ķŚ«ķ󜵌Č׫▒µā│ÕQ?#8220;µłæń¤źķüō’╝īµłæÕ░åõĮ┐ńö©µŁŻÕłÖĶĪ©ĶŠŠÕ╝ÅŃĆ?#8221;ńÄ░Õ£©õ╗¢µ£ēõĖżõĖ¬ķŚ«ķóśõ║åŃĆéŌĆöŌĆöJamie Zawinski
sdfond 2010-03-12 13:06 ÕÅæĶĪ©Ķ»äĶ«║
]]>ŃĆÉķóśńø«Õłåµ×ÉŃĆ?br>ŃĆĆŃĆĆÕ»╣õ║ÄŗéŗńøśµöŠĶ×RķŚ«ķóśÕÅ»õ╗źńö©ń╗äÕÉłµĢ░ÕŁ”ńÜäń¤źĶ»åµØźĶ¦ŻÕå╗I╝īõĮåµś»Õ»╣õ║ÄÕɽń”üÕī║ńÜäµæåµöŠķŚ«ķóśÕQīĶÖĮńäČń╗äÕÉłµĢ░ÕŁ”ń╗ÖÕć▐Z║åŠlÅÕģĖńÜ䵯ŗńøśÕżÜÖÕ╣Õ╝Å+Õ«ęÄ¢źÕĤńÉåńÜäĶ¦Żµ│Ģ’╝īõĮåµś»Õ«×ķÖģõĖŁµŻŗńøśÕżÜÖÕ╣Õ╝ÅńÜäµ▒éĶ¦Żµś»ÕŠłÕø░ķÜäĪÜäÕQīÕøĀµŁżõĖĆĶł¼ķ£ĆĶ”üÕƤÕŖ®ńŖȵĆüÕÄŗŠ~®ÕŖ©µĆüĶ¦äÕłÆµ▒éĶ¦ŻŃĆ?br>ŃĆĆŃĆĆńÄ░Õ£©ķóśńø«õĖŁĶ”üµ▒éÕć║õ║ÆõĖŹµöšdć╗ńÜäĶ▒ĪńÜäµ¢╣µ│ĢµĢ░ÕQīĶ▒ĪńÜäµö╗Õć╗ĶĄ\ŠU┐µś»µ¢£ńÜäÕQīµś»õĖŹµś»ÕÅ»õ╗źĶĆāĶÖæķććńö©µöŠĶ×RńÜäµ¢╣µ│ĢµØźĶ¦ŻÕæóÕQ¤Õ░åŗéŗńøśķ╗æńÖĮµ¤ōĶē▓ÕQīÕ”éµ×£õĖĆõĖ¬Ķ▒ĪÕ£©ķ╗æĶē▓ńÜäµĀ╝ÕŁÉķćīķØóÕQīķéŻõ╣łÕ«āõĖĆÕ«ÜõĖŹõ╝ܵö╗Õćšdł░ńÖĮĶē▓ńÜäµĀ╝ÕŁÉ’╝īśqÖµĀĘńÜäĶ»ØÕÅ»õ╗źÕłåÕ╝ĆĶ«ĪµĢ░ÕQīńäČÕÉĵ£ĆÕÉÄÕł®ńö©õ╣śµ│ĢÕĤńÉåÕŖĀĶĄõhØź×«▐pĪīõ║åŃĆéµŖŖŗéŗńøśµŚŗĶØ{45Õ║”’╝īśqÖµĀĘĶ▒ĪńÜäµöšdć╗ĶĘ»ń║┐׫▒µś»ńø┤ńÜäõ║å’╝īÕ”éµ×£ÕŬĶĆāĶÖæõĖĆ┐UŹķó£Ķē▓ńÜäĶ»Ø’╝īķéŻõ╣łķŚ«ķóś×«▐pØ{ÕÅśµłÉõ║åń╗ÅÕģĖńÜäµöŠĶ×RķŚ«ķóśõ║å’╝īÕÅ»õ╗źÕł®ńö©ÕŖ©µĆüĶ¦äÕłÆĶ¦ŻÕå¤ļĆ?br>ŃĆĆŃĆĆĶ«Šdp[i][j]ĶĪ©ńż║ÕēŹiĶĪīµöŠõ║åjõĖ¬Ķ×RńÜäµ¢╣µ│ĢµĢ░ÕQīc[i]ĶĪ©ńż║ĮW¼iĶĪīÕÅ»õ╗źµöŠŠ|«ńÜäŗéŗÕŁÉµĢ░ķćÅÕQīķéŻõ╣łĶØ{┐U└L¢╣ĮEŗõžōÕQ?br>ŃĆĆŃĆĆŃĆĆŃĆĆdp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (c[i] - (j - 1))
ŃĆĆŃĆĆķ£ĆĶ”üµ│©µäÅńÜ䵜»cµĢ░ń╗äÕ║öĶ»źµś»Õó×Õ║ÅńÜäÕQīĶ┐ÖµĀõhēŹĶāĮõ┐ØĶ»üÕēŹķØóńÜäj-1ĶĪīµöŠõ║åĶ×RÕQīÕ»╣Õ║öĶ┐ÖõĖĆĶĪīÕ░▒µ£ēj-1õĖ¬õĮŹŠ|«õĖŹÕÅ»µöŠõ║åŃĆ?br>ŃĆĆŃĆĆśqÖõĖ¬ķóśńø«ńÜädpµ¢╣ń©ŗõĖŹķÜŠµā╗I╝īõĮåµś»Õ”éõĮĢµŖŖµ©ĪÕ×ŗĶØ{Õī¢Õł░µöŠĶ×RķŚ«ķ󜵜»õĖŹÕ«ęÄśōµāø_ł░ńÜä’╝ī׫żÕģȵś»Õ░åŗéŗńøśķ╗æńÖĮµ¤ōĶē▓ÕÉÄÕłåÕ╝ĆĶ«ĪµĢ░ńÜäµā│µ│Ģ’╝īķØ×ÕĖĖÕĘ¦Õ”ÖŃĆ?br>
ķóśńø«õ╗ŻńĀüÕQ?
1 #include <iostream>
2 #include <algorithm>
3 using namespace std;
4 const int N = 70;
5
6 void init(int n, int c1[N], int c2[N])
7 {
8 memset(c1, 0, sizeof(int) * N);
9 memset(c2, 0, sizeof(int) * N);
10 for (int i = 1; i <= n; i++)
11 {
12 for (int j = 1; j <= n; j++)
13 {
14 if ((i + j) & 1)
15 c2[(i+j)/2]++;
16 else
17 c1[(i+j)/2]++;
18 }
19 }
20 }
21 void bishops(int n, int dp[N][N], int c[N])
22 {
23 for (int i = 0; i <= n; i++)
24 dp[i][0] = 1;
25 for (int i = 1; i <= n; i++)
26 for (int j = 1; j <= c[i]; j++)
27 dp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (c[i] - j + 1);
28 }
29
30 int main()
31 {
32 int n, k, c1[N], c2[N], dp1[N][N], dp2[N][N], ans;
33
34 while (scanf("%d %d", &n, &k) == 2)
35 {
36 if (n == 0 && k == 0)
37 break;
38 init(n, c1, c2);
39 sort(c1 + 1, c1 + n + 1);
40 sort(c2 + 1, c2 + n);
41 memset(dp1, 0, sizeof(dp1));
42 memset(dp2, 0, sizeof(dp2));
43 bishops(n, dp1, c1);
44 bishops(n - 1, dp2, c2);
45 ans = 0;
46 for (int i = 0; i <= k; i++)
47 ans += dp1[n][i] * dp2[n-1][k-i];
48 printf("%d\n", ans);
49 }
50
51 return 0;
52 }
2 #include <algorithm>
3 using namespace std;
4 const int N = 70;
5
6 void init(int n, int c1[N], int c2[N])
7 {
8 memset(c1, 0, sizeof(int) * N);
9 memset(c2, 0, sizeof(int) * N);
10 for (int i = 1; i <= n; i++)
11 {
12 for (int j = 1; j <= n; j++)
13 {
14 if ((i + j) & 1)
15 c2[(i+j)/2]++;
16 else
17 c1[(i+j)/2]++;
18 }
19 }
20 }
21 void bishops(int n, int dp[N][N], int c[N])
22 {
23 for (int i = 0; i <= n; i++)
24 dp[i][0] = 1;
25 for (int i = 1; i <= n; i++)
26 for (int j = 1; j <= c[i]; j++)
27 dp[i][j] = dp[i-1][j] + dp[i-1][j-1] * (c[i] - j + 1);
28 }
29
30 int main()
31 {
32 int n, k, c1[N], c2[N], dp1[N][N], dp2[N][N], ans;
33
34 while (scanf("%d %d", &n, &k) == 2)
35 {
36 if (n == 0 && k == 0)
37 break;
38 init(n, c1, c2);
39 sort(c1 + 1, c1 + n + 1);
40 sort(c2 + 1, c2 + n);
41 memset(dp1, 0, sizeof(dp1));
42 memset(dp2, 0, sizeof(dp2));
43 bishops(n, dp1, c1);
44 bishops(n - 1, dp2, c2);
45 ans = 0;
46 for (int i = 0; i <= k; i++)
47 ans += dp1[n][i] * dp2[n-1][k-i];
48 printf("%d\n", ans);
49 }
50
51 return 0;
52 }
µ│©’╝ܵ£¼µ¢ćõĮ£õ║Ä2009“q?µ£?3µŚ?19ńé?1Õł?br>
sdfond 2010-02-06 17:58 ÕÅæĶĪ©Ķ»äĶ«║
]]>ŃĆÉķóśńø«Õłåµ×ÉŃĆ?br>ŃĆĆŃĆĆśqÖõĖ¬ķóśńø«õ╣ŹõĖĆń£ŗµī║ĮÄĆÕŹĢńÜäÕQīõĮåµś»µā│ÕüÜÕ»╣śqśµś»Ķ”üõ╗öŠlåńÜäµĆØĶĆāõĖŗńÜäŃĆéĶĪźķøåĶØ{Õī¢ńÜäµĆصā│ÕQīµ▒éÕć║µēƵ£ēÕģ▒ŠU┐ńÜäõĖēÕģāŠlä’╝īńäČÕÉÄńö©µĆ└LĢ░ÕćŵÄē׫▒µś»Į{öµĪłõ║å’╝īÕģ│ķö«×«▒µś»Õ”éõĮĢµ▒éÕģ▒ŠU┐õĖēÕģāń╗äŃĆéxÕØɵĀćńøĖÕÉīÕÆīyÕØɵĀćńøĖÕÉīńÜäµ»öĶŠāÕźĮĶ«Īń«ŚÕQīÕ£©õĖƵØĪµ¢£ŠU┐ńÜä׫ūāĖŹÕźĮń«Śõ║å’╝īńöųMĖ¬ÕøæųÅæńÄÄ═╝īÕŹ│õŗ╔µ¢£ńÄćńøĖÕÉīńÜäń║┐ÕQīń╗ÅśqćńÜäµĀ╝ńé╣µĢ░ÕÅ»ĶāĮÕÉäõĖŹńøĖÕÉīŃĆéµĆØĶĄ\ÕĮōńäČśqśµś»µ×ÜõŗDy / xÕQłõĖŹÕÉīńÜäy / x╝ŗ«Õ«Üõ║åõĖŹÕÉīńÜäń¤®Õ┼×Õī║Õ¤¤ÕQē’╝īõ╣ŗÕÉÄÕ”éõĮĢµ£ēµĢłńÜäĶ«ĪĮÄŚ’╝īµłæķććńö©ńÜäµ¢ęÄ│ĢÕÅ»ĶāĮµ£ēõ║øķ║╚Øā”ÕQīµ£ēńé╣ń▒╗Õ«ęÄ¢źńÜäµ¢╣µ│ĢŃĆéõ╗źµ¢£ńÄćõĖ║a / bõĖ▐ZŠŗÕQ?a, b) = gÕQīķéŻõ╣łm * nńÜäÕī║Õ¤¤ÕåģõĖĆիܵ£ē(m - a + 1) * (n - b + 1)õĖ¬ķéŻõ╣łÕż¦ńÜäń¤®ÕĮó’╝īśqÖµĀĘńÜäń¤®ÕĮóń╗ÅśqćńÜäµĀ╝ńé╣µĢ░µś»(g + 1)ÕQøńäČÕÉÄÕøĀõĖ║ÕÉīĮ{ēµ¢£ńÄćÕ░ÅõĖĆńé╣ńÜäń¤®Õ┼×(a - a / g, b - b / g)õ╣¤µś»ÕŁśÕ£©ńÜä’╝īõĖ¬µĢ░ÕÉīµĀĘÕÅ»õ╗źŠl¤Ķ«ĪÕć║µØźÕQīõĮåµś»µ£ēõ║øÕż¦ń¤®Õ┼×Õīģµŗ¼õ║å’╝īĶ”üÕÄ╗µÄē’╝øÕøĀµŁż×«▒ķććńö©Ķ┐Ö┐UŹµĆصā│ÕQīÕģłµ▒éÕć║Õż¦ń¤®ÕĮóńÜäõĖ¬µĢ░ÕQīńäČÕÉÄõŠØŗŲĪÕŠĆõĖŗÕćÅÕQīÕ░▒ÕÅ»õ╗źķü┐ÕģŹķćŹÕżŹĶ«ĪµĢ░õ║åŃĆéĶÖĮńäČĶ┐ÖµĀĘÕżŹµØéÕ║”µ£ēńé╣ķ½ś’╝īõĖŹĶ┐ćµ×üķÖɵĢ░µŹ«śqśµś»µ»öĶŠāÕ┐½ńÜäĶĘæÕć║µØźõ║åŃĆ?br>ŃĆĆŃĆĆĶ»┤ńÜäÕÅ»ĶāĮõĖŹÕż¬µĖģµźÜÕQīÕģĘõĮōõ╗ŻńĀüÕ”éõĖŗ’╝Ü
1 #include <cstdio>
2 #include <iostream>
3 using namespace std;
4 const int N = 1024;
5
6 bool tag[N][N];
7 long long calc(long long n)
8 {
9 if (n <= 2)
10 return 0;
11 return n * (n - 1) * (n - 2) / 6;
12 }
13 int gcd(int a, int b)
14 {
15 return b == 0 ? a : gcd(b, a % b);
16 }
17
18 int main()
19 {
20 int m, n, g, a, b, timer = 1, cnt[N], ta, tb;
21 long long ans;
22
23 while (scanf("%d %d", &m, &n) == 2)
24 {
25 memset(tag, 0, sizeof(tag));
26 if (m == 0 && n == 0)
27 break;
28 ans = calc((m + 1) * (n + 1)) - calc(m + 1) * (n + 1) - calc(n + 1) * (m + 1);
29 for (int i = m; i >= 1; i--)
30 for (int j = n; j >= 1; j--)
31 {
32 g = gcd(i, j);
33 a = i / g, b = j / g;
34 if (tag[a][b]) continue;
35 memset(cnt, 0, sizeof(cnt));
36 tag[a][b] = 1;
37 a = i, b = j;
38 ta = i / g, tb = j / g;
39 for (int k = g; k >= 2; k--)
40 {
41 cnt[k] += (m - a + 1) * (n - b + 1);
42 ans -= calc(k + 1) * cnt[k] * 2;
43 for (int t = 1; t <= k - 2; t++)
44 cnt[k-t] -= (t + 1) * cnt[k];
45 a -= ta, b -= tb;
46 }
47 }
48 cout << "Case " << timer++ << ": " << ans << endl;
49 }
50
51 return 0;
52 }
53
2 #include <iostream>
3 using namespace std;
4 const int N = 1024;
5
6 bool tag[N][N];
7 long long calc(long long n)
8 {
9 if (n <= 2)
10 return 0;
11 return n * (n - 1) * (n - 2) / 6;
12 }
13 int gcd(int a, int b)
14 {
15 return b == 0 ? a : gcd(b, a % b);
16 }
17
18 int main()
19 {
20 int m, n, g, a, b, timer = 1, cnt[N], ta, tb;
21 long long ans;
22
23 while (scanf("%d %d", &m, &n) == 2)
24 {
25 memset(tag, 0, sizeof(tag));
26 if (m == 0 && n == 0)
27 break;
28 ans = calc((m + 1) * (n + 1)) - calc(m + 1) * (n + 1) - calc(n + 1) * (m + 1);
29 for (int i = m; i >= 1; i--)
30 for (int j = n; j >= 1; j--)
31 {
32 g = gcd(i, j);
33 a = i / g, b = j / g;
34 if (tag[a][b]) continue;
35 memset(cnt, 0, sizeof(cnt));
36 tag[a][b] = 1;
37 a = i, b = j;
38 ta = i / g, tb = j / g;
39 for (int k = g; k >= 2; k--)
40 {
41 cnt[k] += (m - a + 1) * (n - b + 1);
42 ans -= calc(k + 1) * cnt[k] * 2;
43 for (int t = 1; t <= k - 2; t++)
44 cnt[k-t] -= (t + 1) * cnt[k];
45 a -= ta, b -= tb;
46 }
47 }
48 cout << "Case " << timer++ << ": " << ans << endl;
49 }
50
51 return 0;
52 }
53
sdfond 2009-10-15 19:54 ÕÅæĶĪ©Ķ»äĶ«║
]]>ŃĆĆŃĆĆõ╣¤Õ░▒µś»õĖĆõĖ¬Õ«╣µ¢źÕĤńÉåŃĆéńäČÕÉĵĆ╚ØÜäµ£¤µ£øE = sigma{C(n, i) * P(i) * i * n * d}ÕQīi = 0 ... NŃĆ?br>ŃĆĆŃĆĆśqÖõĖ¬Õ╝ÅÕŁÉÕłŚÕć║µØźÕÉĵĆÄõ╣łõ╣¤µ▒éõĖŹÕć║Šlōµ×£ŃĆéµÖÜõĖŖimemsÕæŖĶ»ēõ║åµłæõĖĆõĖ¬ÕŠłĮÄĆÕŹĢńÜäµÄ©Õ»╝µ¢ęÄ│ĢŃĆéÕ»╣õ║ÄõĖĆõĖ¬ÕĢåÕ║ŚµØźĶ»▀_╝īõĖĆõĖ¬õØhõĖŹÕÄ╗ńÜäµ”éńÄ浜»(N - 1) / NÕQīķéŻõ╣łMõĖ¬õØhķāĮõĖŹÕÄ╚ØÜäµ”éńÄ浜?(N - 1) / N) ^ MÕQīńö©1ÕćÅÕÄ╗śqÖõĖ¬Šlōµ×£×«▒µś»Ķé»Õ«ÜĶćø_░æµ£ēõØhÕÄ╗Ķ┐ÖõĖ¬ÕĢåÕ║ŚńÜäµ”éńÄćŃĆéńäČÕÉĵĆ╚ØÜäµ£¤µ£ø׫ūā╣śõ╗źNõĖ¬ÕĢåÕ║Ś’╝īÕåŹõ╣śõ╗źĶĄÜķÆ▒µĢ░n * d׫▒ÕÅ»õ╗źõ║åŃĆéÕŠłÕĘ¦Õ”ÖÕQīÕøĀõĖ▐Z╗¢µś»õ╗ÄÕĢåÕ║ŚńÜäĶ¦ÆÕ║”ńø┤µÄźĶĆāĶÖæńÜäķŚ«ķóś’╝īĶĆīõĖŹĶĆāĶÖæÕĢåÕ║ŚńÜäõØhµĢÄ═╝īśqÖµĀĘ׫ūāĖŹńö©ÕłŚµ”éńÄćÕłåÕĖāõ║åŃĆ?br>ŃĆĆŃĆĆõĮåµś»õĖŖķØóńÜäÕģ¼Õ╝ÅÕ░▒õĖŹĶāĮµÄ©Õ»╝Õć║µŁŻ╝ŗ«ń╗ōµ×£õ║åõ╣ł’╝īÕÉÄµØźÕÅłµÄ©õ║åõĖĆõĖŗ’╝īÕÅæńÄ░µś»ÕÅ»õ╗źńÜäÕQłńģ¦ńØĆŠlōµ×£ńī? -!ÕQēŃĆ?br>ŃĆĆŃĆĆÕģĘõĮōńÜäµÄ©Õ»╝ÕŠłķ║╚Øā”ÕQīõĮåµś»µĆ╚ØÜäµØźĶ»┤ńö©Õł░õ║åń╗äÕÉłµĢ░ÕŁ”ńÜäÕćĀõĖ¬Õģ¼Õ╝ÅŃĆéķ”¢Õģ?nbsp;k * C(n, k) = n * C(n - 1, k - 1)ÕQīÕł®ńö©Ķ┐ÖõĖ¬Õģ¼Õ╝ŵŖŖÕż¢ķØóńÜäiµČłÕÄ╗ŃĆéńäČÕÉĵ£ēpascalķĆƵĩÕ╝Å’╝ÜC(n, k) = C(n - 1, k) + C(n - 1, k - 1)ŃĆ鵳æõ╗¼ÕłåÕł½ĶĆāĶÖæ(i / N) ^ MÕēŹķØóńÜäń│╗µĢÄ═╝īÕÅ»õ╗źÕÅæńÄ░ķāĮµś»õĖżõĖ¬õ║īķĪ╣Õ╝Åń│╗µĢ░ńøĖõ╣śńÜäµ¢╣Õ╝ÅŃĆéµŖŖÕģČõĖŁńÜäõĖĆõĖ¬Õł®ńö©pascalÕģ¼Õ╝ÅÕ▒ĢÕ╝ĆÕÉÄ’╝īÕć║ńÄ░õ║åÕ┼×Õ”éC(n, 0) - C(n, 1) + C(n, 2) - ...õ╣ŗń▒╗ńÜäÕ╝ÅÕŁÉ’╝īŠlōµ×£µś?ÕQīµČłÕÄųM║åŃĆéÕē®õĖŗńÜäśqśµś»õĖżõĖ¬õ║īķĪ╣Õ╝Åń│╗µĢ░ńÜäõ╣śń¦»ÕQīõĖŹśqćķāĮµś»Ķ┐Ö┐UŹÕ┼×Õ╝ÅńÜäÕQÜC(n, k) * C(k, r)ÕQīÕ«āĮ{ēõ║ÄC(n, r) * C(n - 1, k - 1)ŃĆéĶ┐ÖµĀĘÕÅśÕĮóõ╣ŗÕÉĵ£ēõĖĆõĖ¬Õģ¼Õģ▒ķĪ╣׫▒ÕÅ»õ╗źµÅÉÕć║ÕÄ╗õ║å’╝īķćīķØóśqśµś»ÕĮóÕ”é(1 - 1) ^ nńÜäÕ┼×Õ╝ÅŃĆéĶ┐ÖµĀ’L╗ōµ×£Õ░▒µś?ŃĆéÕ£©Ķ«Īń«ŚõĖŗõĖĆÖÕ╣ńÜäŠp└LĢ░ńÜ䵌ČÕĆÖ’╝īĮW¼õĖĆŗŲĪÕ▒ĢÕ╝ĆÕÉÄķćīķØóµü░ÕźĮÕīģÕɽõ║åÕēŹõĖĆÖÕ╣ńÜäŠp└LĢ░ÕQīńø┤µÄźÕ░▒µś?µČłÕÄ╗õ║å’╝īńäČÕÉÄŠl¦ń«ŗÕł®ńö©õĖŖķØóńÜäµ¢╣µ│ĢÕ▒ĢÕ╝ĆŃĆéõĖŁķŚ┤µÄ©Õ»╝ńÜäśqćń©ŗõĖŁĶ┐śķ£ĆĶ”üµĘ╗ÕŖĀõĖĆõ║øÕĆķgžō0ńÜäķĪ╣õŠ┐õ║ÄŠl¦ń«ŗńÜäµÄ©Õ»╣{Ć?br>ŃĆĆŃĆĆśqÖõĖ¬µ¢ęÄ│ĢÕŠłķ║╗ńā”’╝īõĖŹĶ┐ćµÄ©Õ»╝śqćń©ŗõĖŁĶ┐śµś»ńö©ÕłŅC║åÕŠłÕżÜń¤źĶ»åńÜä’╝ī׫▒ÕĮōÕżŹõ╣Āõ║? -!ÕģČÕ«×śqÖõĖ¬µÄ©Õ»╝Ķ”üõĖŹµś»ń¤źķüōõ║åµ£ĆÕÉÄńÜäÕģ¼Õ╝Åõ╣¤õĖŹµĢóµÄ©ÕQīÕ«×Õ£©Õż¬ķ║╚Øā”ÕQīń£ŗµØźĶ┐śµś»Õ¤║µ£¼ÕŖ¤ŗŲĀń╝║ÕĢŖ’╝īĶĆīõĖöĮÄŚµ”éńÄćńÜäķóśńø«śqśµś»Ķ”üÕżÜŠlāõ╣ĀŠlāõ╣ĀŃĆéÕÅ”Õż¢µ│©µäŵĆØń╗┤ńÜäńüĄŗz└LƦ’╝īÕģČÕ«×ĮÄĆÕŹĢÕüܵ│ĢõĖŹķÜŠµā│ÕQīõĮåµś»µ£ĆÕ╝ĆÕ¦ŗĶó½ÕÉēÕż¦ńēøĶ»»Õ»ķg║åÕQīÕ░▒ńö©õ║åõĖĆõĖ¬õĖźµĀ╝ńÜäµÄ©Õ»╝µ¢ęÄ│ĢÕQīńŗ¼ń½ŗµĆØĶĆāĶ┐śµś»ÕŠłķćŹĶ”üńÜäŃĆ?br>
ķóśńø«õ╗ŻńĀüÕQ?br>
1 #include <cstdio>
2 #include <cmath>
3
4 int main()
5 {
6 double N, M, n, d;
7
8 while (scanf("%lf %lf %lf %lf", &N, &M, &n, &d) == 4)
9 printf("%.3lf\n", n * d * N * (1.0 - pow(1.0 - 1.0 / N, M)));
10
11 return 0;
12 }
13
2 #include <cmath>
3
4 int main()
5 {
6 double N, M, n, d;
7
8 while (scanf("%lf %lf %lf %lf", &N, &M, &n, &d) == 4)
9 printf("%.3lf\n", n * d * N * (1.0 - pow(1.0 - 1.0 / N, M)));
10
11 return 0;
12 }
13
sdfond 2009-06-18 21:48 ÕÅæĶĪ©Ķ»äĶ«║
]]>ŃĆÉń«Śµ│ĢÕłåµ×ÉŃĆ?br>ŃĆĆŃĆƵä¤Ķ¦ēµ╗ĪµüČÕ┐āńÜäõĖĆõĖ¬ķóśńø«’╝īķ£ĆĶ”üń¢»ńŗéńÜäµēŠĶ¦äÕŠŗŃĆéķ”¢ÕģłÕ«╣µśōń£ŗÕć°ÖĄ\ÕŠäµĢ░µś»õĖĆõĖ¬ń╗äÕÉłµĢ░ÕQīÕŲłõĖöµ»ÅõĖĆÕ▒éķāĮµś»µ©ĪÕģŁÕ¾@ńÄ»ńÜäŃĆéõĮåµś»µĆĵĀʵēæųł░Õ▒éµĢ░ÕQłõ╣¤×«▒µś»µ£Ćń¤ŁĶĄ\ÕŠäķĢ┐Õ║”’╝ēÕæó’╝¤µ£ĆÕ╝ĆÕ¦ŗµā│Õ╗║ń½ŗÕØɵĀćŠp╚ØäČÕÉÄÕł®ńö©ÕćĀõĮĢµ¢╣µ│Ģń«ŚÕć║µØźÕQīõĮåµś»Õ”éõĮĢµŚĀĶ«║µś»ĮWøÕŹĪ׫öÕØɵĀćń│╗śqśµś»µ×üÕØɵĀćń│╗ńÜäÕŠÅń½ŗķāĮµś»Õø░ķÜäĪÜäÕQøńäČÕÉĵā│ÕŁśÕøŠ“q┐µÉ£ÕQīÕÅæńÄ░ń®║ķŚ┤õĖŹÕż¤ŃĆéÕÉÄµØźÕÅæńÄÄ═╝īµŖŖÕøŠÖÕ║µŚČķÆłĶØ{90Õ║”’╝īÕć║ńÄ░õ║åõĖĆõĖ¬ÕŠłµ£ēµäŵĆØńÜäĶ¦äÕŠŗŃĆéõ╗źÕĤńé╣ÕQłµĢ░ÕŁŚõžō1ÕQēõžōõĖŁÕ┐āÕ╗║ń½ŗÕØɵĀćŠp╗’╝īõĖŹĶ┐ćÕØɵĀćńÜäķĆēÕÅ¢ķ£ĆĶ”üõĖĆõ║øµŖĆÕʦŃĆéÕÅ»õ╗źń£ŗÕć║µĢ░ÕŁŚµś»õĖĆÕ▒éÕ▒éÕłåÕĖāńÜä’╝īÕÅ¢xÕĘ”ĶŠ╣ńÜäńé╣ÕØɵĀćõĖ║’╝ł-2ÕQ?ÕQē’╝īõ╗źÕÉĵ»ÅÕŠĆÕĘ”Õó×ÕŖĀõĖĆÕ▒é’╝īµ©¬ÕØɵĀćÕ░▒ÕÅśÕī¢2ŃĆéÕģČÕ«×ÕÆīÕĤńé╣ŠUĄÕØɵĀćńøĖÕÉīõĖöõĮŹõ║ÄÕģČÕĘ”ĶŠ╣ńÜäńéęÄü░ÕźĮµś»µ»ÅõĖĆÕ▒éµĢ░ÕŁŚµ£ĆÕż¦ńÜäŠlōńé╣ÕQüĶ┐ÖµĀĘÕŬĶ”üńĪ«Õ«Üõ║åśqÖõĖ¬ńé╣’╝īÕÅ»õ╗źµīēńģ¦ķĆåµŚČķÆłńÜäÖÕ║Õ║ÅõŠØµ¼ĪŠlÖĶ┐ÖõĖĆÕ▒éńÜäµēƵ£ēńé╣ńÜäÕØɵĀćµÄ©Õć║µØźŃĆéĶ┐ÖµĀ°P╝īŠlÖÕ«ÜõĖĆõĖ¬µĢ░ÕŁŚ’╝īµłæõ╗¼ÕÅ»õ╗źµĀęÄŹ«µ»ÅõĖĆÕ▒éµ£ĆÕż¦ńÜäµĢ░ÕŁŚµÄ©Õć║śqÖõĖ¬µĢ░ńÜäÕØɵĀćŃĆ?br>ŃĆĆŃĆĆńÄ░Õ£©µ£ēõ║åÕØɵĀćÕQłÕÅ»õ╗źń£ŗµłÉµś»µø╝ÕōłÖÕ┐ÕØɵĀć’╝ēÕQīÕ░▒ÕÅ»õ╗źµÄ©µĄŗĶĘ»ÕŠäõ║åŃĆéµŖŖõĖżõĖ¬µĢ░ÕŁŚńÜäÕØɵĀćµ▒éÕĘ«’╝ī׫▒ÕÅ»õ╗źń£ŗµłÉµś»õĖĆõĖ¬Õ£©ÕĤńé╣õ║åŃĆéÕØɵĀćÕÆīĶĘ»ÕŠäńÜäÕģ│ŠpųMĖŹµś»ÕŠłÕźĮµēŠÕQīÕåÖõ║?ŃĆ?ĶĪīÕÅæńÄŅC║åõĖĆõĖ¬ÕŠłĶ»ĪÕ╝éńÜäĶ¦äÕŠŗŃĆéÕģłµŖŖÕØɵĀćÕī¢µłÉµŁŻńÜä’╝īńäČÕÉÄÕÅæńÄ░x >= yńÜ䵌ČÕĆÖÕ░▒µś»C( (x + y) / 2, y)ÕQīÕÉ”ÕłÖµś»C( y, (y - x) / 2)ŃĆéõ╣ŗÕÉÄÕ░▒µś»ķ½śŠ_æų║”õ║åŃĆ?br>
ķóśńø«õ╗ŻńĀüÕQ?br>
1 import java.util.*;
2 import java.math.*;
3
4 class point
5 {
6 int x, y;
7 public point(int x, int y)
8 {
9 this.x = x;
10 this.y = y;
11 }
12 }
13 class Main
14 {
15 public static void main(String[] args)
16 {
17 Scanner in = new Scanner(System.in);
18 int a, b, len;
19 BigInteger ans;
20 point pa, pb;
21
22 while (in.hasNext())
23 {
24 a = in.nextInt();
25 b = in.nextInt();
26 if (a == 0 && b == 0)
27 break;
28 pa = GetCoordinate(a);
29 pb = GetCoordinate(b);
30 pa.x = pb.x - pa.x;
31 pa.y = pb.y - pa.y;
32 pa.x = pa.x < 0 ? -pa.x : pa.x;
33 pa.y = pa.y < 0 ? -pa.y : pa.y;
34 if (pa.x >= pa.y)
35 {
36 len = (pa.x + pa.y) / 2;
37 ans = C(len, pa.y);
38 }
39 else
40 {
41 len = pa.y;
42 ans = C(len, (pa.y - pa.x) / 2);
43 }
44 System.out.print("There ");
45 if (ans.compareTo(BigInteger.ONE) == 0)
46 System.out.print("is 1 route");
47 else
48 System.out.print("are " + ans + " routes");
49 System.out.println(" of the shortest length " + len + ".");
50 }
51 }
52 static BigInteger C(int n, int k)
53 {
54 BigInteger ret = BigInteger.ONE;
55 if (k > n - k)
56 k = n - k;
57 for (int i = 1; i <= k; i++)
58 {
59 ret = ret.multiply(new BigInteger(new String(n - i + 1 + "")));
60 ret = ret.divide(new BigInteger(new String(i + "")));
61 }
62 return ret;
63 }
64 static point GetCoordinate(int n)
65 {
66 int[][] dir = new int[][]{{1, -1}, {2, 0}, {1, 1}, {-1, 1}, {-2, 0}, {-1, -1}};
67 int i = 0, j = 0, k = 0, tx, ty, cnt = 0, delta;
68 point p = new point(0, 0);
69
70 if (n == 1)
71 return p;
72 for (i = 2; i <= 1000; i++)
73 if ((3 * i * i - 3 * i + 1) >= n)
74 break;
75 delta = 3 * i * i - 3 * i + 1 - n;
76 i--;
77 tx = -2 * i;
78 ty = 0;
79 boolean flag = false;
80 for (j = 0; j < 6; j++)
81 {
82 for (k = 0; k < i; k++)
83 {
84 if (cnt == delta)
85 {
86 flag = true;
87 break;
88 }
89 cnt++;
90 tx += dir[j][0];
91 ty += dir[j][1];
92 }
93 if (flag)
94 break;
95 }
96 p.x = tx;
97 p.y = ty;
98
99 return p;
100 }
101 }
102
2 import java.math.*;
3
4 class point
5 {
6 int x, y;
7 public point(int x, int y)
8 {
9 this.x = x;
10 this.y = y;
11 }
12 }
13 class Main
14 {
15 public static void main(String[] args)
16 {
17 Scanner in = new Scanner(System.in);
18 int a, b, len;
19 BigInteger ans;
20 point pa, pb;
21
22 while (in.hasNext())
23 {
24 a = in.nextInt();
25 b = in.nextInt();
26 if (a == 0 && b == 0)
27 break;
28 pa = GetCoordinate(a);
29 pb = GetCoordinate(b);
30 pa.x = pb.x - pa.x;
31 pa.y = pb.y - pa.y;
32 pa.x = pa.x < 0 ? -pa.x : pa.x;
33 pa.y = pa.y < 0 ? -pa.y : pa.y;
34 if (pa.x >= pa.y)
35 {
36 len = (pa.x + pa.y) / 2;
37 ans = C(len, pa.y);
38 }
39 else
40 {
41 len = pa.y;
42 ans = C(len, (pa.y - pa.x) / 2);
43 }
44 System.out.print("There ");
45 if (ans.compareTo(BigInteger.ONE) == 0)
46 System.out.print("is 1 route");
47 else
48 System.out.print("are " + ans + " routes");
49 System.out.println(" of the shortest length " + len + ".");
50 }
51 }
52 static BigInteger C(int n, int k)
53 {
54 BigInteger ret = BigInteger.ONE;
55 if (k > n - k)
56 k = n - k;
57 for (int i = 1; i <= k; i++)
58 {
59 ret = ret.multiply(new BigInteger(new String(n - i + 1 + "")));
60 ret = ret.divide(new BigInteger(new String(i + "")));
61 }
62 return ret;
63 }
64 static point GetCoordinate(int n)
65 {
66 int[][] dir = new int[][]{{1, -1}, {2, 0}, {1, 1}, {-1, 1}, {-2, 0}, {-1, -1}};
67 int i = 0, j = 0, k = 0, tx, ty, cnt = 0, delta;
68 point p = new point(0, 0);
69
70 if (n == 1)
71 return p;
72 for (i = 2; i <= 1000; i++)
73 if ((3 * i * i - 3 * i + 1) >= n)
74 break;
75 delta = 3 * i * i - 3 * i + 1 - n;
76 i--;
77 tx = -2 * i;
78 ty = 0;
79 boolean flag = false;
80 for (j = 0; j < 6; j++)
81 {
82 for (k = 0; k < i; k++)
83 {
84 if (cnt == delta)
85 {
86 flag = true;
87 break;
88 }
89 cnt++;
90 tx += dir[j][0];
91 ty += dir[j][1];
92 }
93 if (flag)
94 break;
95 }
96 p.x = tx;
97 p.y = ty;
98
99 return p;
100 }
101 }
102
sdfond 2009-06-16 22:12 ÕÅæĶĪ©Ķ»äĶ«║
]]>#include <cstdio>
const int N = 10010;
int main()
{
int a[N], n, mod[N] = {0}, tmp = 0, len = 0, pos;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
if (len) continue;
tmp = (tmp + a[i]) % n;
if (tmp == 0)
{
len = i;
pos = 1;
}
if (mod[tmp])
{
len = i - mod[tmp];
pos = mod[tmp] + 1;
}
else
mod[tmp] = i;
}
printf("%d\n", len);
for (int i = 0; i < len; i++)
printf("%d\n", a[pos+i]);
return 0;
}
const int N = 10010;
int main()
{
int a[N], n, mod[N] = {0}, tmp = 0, len = 0, pos;
scanf("%d", &n);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
if (len) continue;
tmp = (tmp + a[i]) % n;
if (tmp == 0)
{
len = i;
pos = 1;
}
if (mod[tmp])
{
len = i - mod[tmp];
pos = mod[tmp] + 1;
}
else
mod[tmp] = i;
}
printf("%d\n", len);
for (int i = 0; i < len; i++)
printf("%d\n", a[pos+i]);
return 0;
}
sdfond 2009-06-12 09:09 ÕÅæĶĪ©Ķ»äĶ«║
]]> 1 #include <cstdio>
2 const int N = 12;
3
4 int p[N], ans;
5 long long gcd(long long a, long long b)
6 {
7 return b == 0 ? a : gcd(b, a % b);
8 }
9 void calc_sg(long long tol, int m, int dep, long long v, bool mark)
10 {
11 if (dep == m)
12 {
13 if (mark) ans -= tol / v;
14 else ans += tol / v;
15 return;
16 }
17 calc_sg(tol, m, dep + 1, v, mark);
18 if (v <= tol)
19 calc_sg(tol, m, dep + 1, v / gcd(v, p[dep]) * p[dep], mark ^ 1);
20 }
21
22 int main()
23 {
24 int T, m, n, a, g;
25
26 scanf("%d", &T);
27 while (T--)
28 {
29 g = 0;
30 bool mark = 1;
31 scanf("%d %d", &m, &n);
32 for (int i = 0; i < m; i++)
33 scanf("%d", &p[i]);
34 for (int i = 0; i < n; i++)
35 {
36 scanf("%d", &a);
37 if (!mark) continue;
38 ans = 0;
39 calc_sg(a, m, 0, 1, 0);
40 g ^= ans;
41 for (int j = 0; j < m; j++)
42 if (a % p[j] == 0)
43 {
44 mark = 0;
45 break;
46 }
47 }
48 if (!mark) puts("Xiao Hong");
49 else printf("%s\n", g ? "Xiao Hong" : "Xiao Gang");
50 }
51
52 return 0;
53 }
54
2 const int N = 12;
3
4 int p[N], ans;
5 long long gcd(long long a, long long b)
6 {
7 return b == 0 ? a : gcd(b, a % b);
8 }
9 void calc_sg(long long tol, int m, int dep, long long v, bool mark)
10 {
11 if (dep == m)
12 {
13 if (mark) ans -= tol / v;
14 else ans += tol / v;
15 return;
16 }
17 calc_sg(tol, m, dep + 1, v, mark);
18 if (v <= tol)
19 calc_sg(tol, m, dep + 1, v / gcd(v, p[dep]) * p[dep], mark ^ 1);
20 }
21
22 int main()
23 {
24 int T, m, n, a, g;
25
26 scanf("%d", &T);
27 while (T--)
28 {
29 g = 0;
30 bool mark = 1;
31 scanf("%d %d", &m, &n);
32 for (int i = 0; i < m; i++)
33 scanf("%d", &p[i]);
34 for (int i = 0; i < n; i++)
35 {
36 scanf("%d", &a);
37 if (!mark) continue;
38 ans = 0;
39 calc_sg(a, m, 0, 1, 0);
40 g ^= ans;
41 for (int j = 0; j < m; j++)
42 if (a % p[j] == 0)
43 {
44 mark = 0;
45 break;
46 }
47 }
48 if (!mark) puts("Xiao Hong");
49 else printf("%s\n", g ? "Xiao Hong" : "Xiao Gang");
50 }
51
52 return 0;
53 }
54
sdfond 2009-06-02 16:01 ÕÅæĶĪ©Ķ»äĶ«║
]]>polyaķóśńø«ÕQ?br>HOJ 2084 The Colored Cubes
HOJ 2647 Megaminx
POJ 1286 Necklace of Beads
POJ 2409 Let it Bead
TOJ 2795 The Queen's New Necklaces
HDU 1812 Count the Tetris
UVa 11255 Necklace
POJ 2154 Color
POJ 2888 Magic Bracelet
UVa 10601 Cubes
NUAA 1110
sdfond 2009-05-12 11:20 ÕÅæĶĪ©Ķ»äĶ«║
]]>ÕģČõĖŁA =(Ak-1 Ak-2 ... A1)ÕQīIµś»ÕŹĢõĮŹń¤®ķś³cĆ?br>ńäČÕÉĵ×äķĆĀõĖĆõĖ¬k * 1ÕłŚÕÉæķćÅbÕQ?br>
śqÖµĀĘÕQīM * bõ╣ŗÕÉÄb0ńÜäÕĆ╝Õ░▒µś»f(k)ÕQīõ╗źµŁżń▒╗µÄ©’╝īM ^ n * bõ╣ŗÕÉÄb0ńÜäÕĆ╝Õ░▒µś»f(k-1+n)ÕQīń«Śµ│ĢÕżŹµØéÕ║”O(k ^ 3 * logn)ŃĆ?br>
sdfond 2009-05-08 22:08 ÕÅæĶĪ©Ķ»äĶ«║
]]>1.µÄÆÕłŚŠläÕÉłõĖÄÕ«╣µ¢źÕĤńÉ?br>µÄÆÕłŚŠläÕÉłķćīķØóńÜ?õĖ¬ķćŹĶ”üńÜäÕ¤║µ£¼ÕĤńÉåÕQÜÕŖĀµ│ĢÕĤńÉåŃĆüõ╣śµ│ĢÕĤńÉåŃĆüÕćŵ│ĢÕĤńÉåŃĆüķÖżµ│ĢÕĤńÉ?br>ÕēŹķØóõĖżõĖ¬µ£ĆõĖ║Õ¤║µ£¼’╝īÕÉÄķØóõĖżõĖ¬µś»µĀ╣µŹ«ÕēŹõĖżõĖ¬ŗzäĪö¤Õć║µØźńÜäŃĆéõ╣śµ│ĢÕĤńÉåµ£ēńÜ䵌ČÕĆÖńÜäÕ║öńö©ÕŠłÕķyÕ”Ö’╝īÕÅ»õ╗źõĮ£õžōõĖĆ┐UŹµēōÕ╝ƵĆØĶĄ\ńÜäÕŖ×µ│ĢŃĆ?br>Õ¤║µ£¼ńÜäµÄÆÕłŚń╗äÕÉłõ╣ŗÕÉÄ’╝īµÄźõĖŗµØźÕ╝ĢÕć▐Z║åÕżÜķćŹķøåŃĆéÕżÜķćŹķøåńÜäµÄÆÕłŚń╗äÕÉłµś»õĖĆõĖ¬ÕŠłŠlÅÕģĖńÜäķŚ«ķóś’╝īµĆ╚Ø╗ōÕ”éõĖŗÕQ?br>ÕżÜķćŹķøåńÜäµÄÆÕłŚÕQ?br>ŃĆĆŃĆĆÕģ©µÄÆÕłŚńÜäĶ»ØÕŬķ£ĆÕ║öńö©ķÖżµ│ĢÕĤńÉå׫▒ÕÅ»õ╗źõ║åŃĆénõĖ¬Õģāń┤ĀńÜäÕżÜķćŹķøåńÜärµÄÆÕłŚķ£ĆĶ”üÕł®ńö©µīćµĢ░ńö¤µłÉÕćĮµĢ░µØźÕüÜŃĆ?br>ÕżÜķćŹķøåńÜäŠläÕÉłÕQ?br>ŃĆĆŃĆĆnõĖ¬Õģāń┤ĀńÜäÕżÜķćŹķøåńÜärŠläÕÉłÕQīÕ”éµ×£r׫Åõ║ÄĮ{ēõ║Äõ╗ųMĮĢõĖĆõĖ¬Õģāń┤ĀÕÅ»ķĆēńÜäõĖ¬µĢ░ÕQīķéŻõ╣łÕ░▒ÕĮÆń╗ōõĖ║ń╗ÅÕģĖńÜäõĖŹÕ«Üµ¢╣ń©ŗńÜäĶ¦ŻµĢ░ķŚ«ķóś’╝īÕÅ»õ╗źÕł®ńö©“ķÜöµØ┐µ│?#8221;µØźÕüÜŃĆéń╗ōµ×£Õ░▒µś»õĖĆõĖ¬ń╗äÕÉłµĢ░ŃĆéÕ”éµ×£rÕż¦õ║ĵ¤Éõ║øÕģāń┤ĀńÜäÕÅ»ķĆēõĖ¬µĢÄ═╝īķéŻõ╣łõĖĆ┐UŹµ¢╣µ│Ģµś»Õł®ńö©Õ«ęÄ¢źÕĤńÉåÕQīõĖĆ┐UŹµ¢╣µ│ĢĶ┐śµś»Ķ”üõŠØķØĀńö¤µłÉÕćĮµĢ░ÕQłń╝¢ĮEŗÕ║ÅńÜ䵌ČÕĆÖÕÅ»õ╗źńö©ÕŖ©ÕĮÆÕüÜ’╝ēŃĆ?br>Õ”éµ×£µś»õĖĆõĖ¬ńÄ»ÕĮóńÜäµÄÆÕłŚŠläÕÉłÕQīķéŻõ╣łķŚ«ķóśÕ░▒Õø░ķÜŠĶ«ĖÕżÜÕQīĶ”üÕł®ńö©Š|«µŹóŠ¤żÕÆīpolyaÕ«ÜńÉåŃĆ?br>ŃĆĆŃĆĆÕŹĢń║»ńÜäõŠØķØĀÕøøÖÕ╣Õ¤║µ£¼ÕĤńÉåµØźĶ«ĪµĢ░ÕQīµ£ēńÜ䵌ČÕĆÖõ╝ܵśæųŠŚÕŖøõĖŹõ╗ÄÕ┐āÕQīĶ┐ÖõĖ¬µŚČÕĆÖÕ░▒ķ£ĆĶ”üÕ«╣µ¢źÕĤńÉåńÜäÕĖ«ÕŖ®ŃĆéÕ«╣µ¢źÕĤńÉåńē╣Õł½ķĆéÕÉłĶ¦ŻÕå│ĶŗźÕ╣▓ķÖÉÕłČµØĪõÜgńÜäõ║żŃĆüÕŲłķŚ«ķóśÕQīõ╣¤µś»µēōÕ╝ƵĆØĶĄ\ńÜäõĖĆ┐UŹµ¢╣µ│ĢŃĆ?br>ŃĆĆŃĆĆÕł®ńö©Õ«ęÄ¢źÕĤńÉåĶ¦ŻÕå│ńÜäń╗ÅÕģöRŚ«ķóśµ£ēÕQÜķöÖµÄÆķŚ«ķóś’╝īÕĖ”ń”üµŁóõĮŹŠ|«ńÜäµÄÆÕłŚŃĆéń”üõĮŹµÄÆÕłŚµĆ╗Ķ¦ēÕŠŚńö©Õ«ęÄ¢źÕĤńÉåĶ¦ŻÕå│ńÜäõĖŹÕż¤õ╝śŠ¤Ä’╝īõĖŹń¤źķüōµ£ēµ▓Īµ£ēÕÅ»õ╗źŠ~¢ń©ŗńÜäµĢ░ÕŁ”µ¢╣µ│ĢŃĆéĶ┐śµ£ēõĖĆõĖ¬Õø░µāæńÜäķŚ«ķóś×«▒µś»Õ«ęÄ¢źÕĤńÉåÕÆīmobiusÕÅŹµ╝öńÜäÕģ│Šp╗’╝īķéŻõĖ¬Õ£░µ¢╣ÕźĮµÖ”µČ®ŃĆéŃĆ?br>ŃĆĆŃĆĆĶʤµÄÆÕłŚń╗äÕÉłńøĖÕģ│ńÜäśqśµ£ē׫▒µś»ńö¤µłÉµÄÆÕłŚÕÆīń╗äÕÉłŃĆéńö¤µłÉµÄÆÕłŚÕł®ńö©ķéŻõĖ¬õ╗Ćõ╣łÕŁŚÕģĖÕ║ŵ│ĢÕźĮÕāÅĶā÷Õż¤õ║åÕQīń╝¢ĮEŗÕźĮÕ«×ńÄ░ŃĆéńö¤µłÉń╗äÕÉłµ¢╣µ│Ģń▒╗õ╝╣{Ć?br>
2.õ║īķĪ╣Õ╝ÅÕ«ÜńÉ?br>µ£ēÕŠłÕżÜÕģ¼Õ╝Å’╝īńö©ńÜ䵌ČÕĆÖÕÅ»õ╗źńÄ░µ¤źŃĆéń╗łõ║Äń¤źķüōõ║åõĖēĶ¦ÆÕĮóµĢ░ÕĤµØźĶʤµÄÆÕłŚń╗äÕÉłµ£ēÕģ╗I╝īĶĆīõĖöµś»õĖĆõĖ¬ÕŠłĮÄĆŗzüńÜäÕģ¼Õ╝ÅŃĆ?br>ÕŠłÕżÜÕģ¼Õ╝ÅńÜäµÄ©Õ»╝ńö©ńÜäµĆصā│ÕŠłÕ”ÖŃĆéµ£ēõĖĆõĖ¬ÕŠłÕźĮńÜäµĆصā│׫▒µś»µŖ?1 + x) ^ nÕł®ńö©õ║īķĪ╣Õ╝ÅÕ«ÜńÉåÕ▒ĢÕ╝ĆÕQīńäČÕÉĵ▒éÕ»╣{Ćüµ▒é┐U»ÕłåÕQīÕ▒ģńäČÕÅ»õ╗źÕ»╝Õć║ÕŠłÕżÜõĖŹÕÅ»µĆØĶ««ńÜäÕģ¼Õ╝ÅŃĆ?br>śqśµ£ēõĖĆõĖ¬ÕŠłķćŹĶ”üńÜäÕ«ÜńÉåÕ░▒µś»pascalÕ«ÜńÉåÕQīpascalķĆƵĩÕ╝ÅÕŠłµ£ēńö©ÕQłÕ▒ĢÕ╝ĆÕÉĵ£ēõĖżń¦ŹÕĮóÕ╝ÅÕQīõĖĆ┐UŹµś»õĖŖõĖŗķÖÉÕØćõĖŹÕ«ÜÕQīõĖĆ┐UŹµś»õĖŗķÖÉõĖŹÕ«ÜÕQē’╝īÕÅ»õ╗źĶ¦ŻÕå│ÕŠłÕżÜŠläÕÉłµĢ░ńÜäµ▒éÕÆīķŚ«ķóśŃĆ?br>ÕÅ”Õż¢õĖĆõĖ¬ķćŹĶ”üńÜäÕ«ÜńÉå׫▒µś»ńēøķĪ┐õ║īķĪ╣Õ╝ÅÕ«ÜńÉå’╝īÕ£©ńö¤µłÉÕćĮµĢŅCĖŁÕ║öńö©“q┐µ│øÕQīÕŻ׫▒µś»µÄ©Õ»╝ĶĄõhØźµ£ēńé╣ŠJüŃĆ?br>
3.ķĆƵĩÕģ│ń│╗ÕÆīńö¤µłÉÕćĮµĢ?br>ŃĆĆŃĆƵ▒éĶ¦ŻŠU┐µĆ¦ķĆƵĩÕģ│ń│╗ńÜäńē╣ÕŠüµ¢╣ĮEŗńÜäµ¢ęÄ│Ģśqśµś»µ£ēõĖĆÕ«ÜõŁhÕĆ╝ńÜäÕQīõĮåµś»ń╝¢ĮEŗõĖŹķĆéńö©ŃĆénĶ¦Żń║┐µĆ¦ķĮÉŗŲĪķĆƵĩµ¢╣ń©ŗµ£ēń¤®ķśĄĶ¦Żµ│ĢŃĆéń©ŹÕŠ«ÕżŹµØéńé╣ńÜäķĆƵĩÕģ│ń│╗ÕQłķØ׊U┐µĆ¦’╝ēÕQīńē╣ÕŠüµ¢╣ĮEŗÕ░▒õĖŹÕż¤ńö©õ║åÕQīÕ┐ģÖÕ╚ØźŁÕć║ńö¤µłÉÕćĮµĢ░Ķ┐ÖõĖ¬µ£ēÕŖøńÜ䵣”ÕÖ©ŃĆéµä¤Ķ¦ēńö¤µłÉÕćĮµĢ░Õ«×Õ£©µś»Õż¬õ╝śŠ¤ÄŃĆüÕż¬Õ╝║Õż¦õ║åŃĆéńö¤µłÉÕćĮµĢ░ńÜäÕģ│ķö«×«▒µś»Ķ”üµŖŖÕżÜķĪ╣Õ╝ŵŗåÕłåµłÉ(1-rx)^nśqÖń¦ŹÕĮóÕ╝ÅÕQīĶ┐ÖµĀĘÕ░▒ÕÅ»õ╗źÕł®ńö©ńēøķĪ┐õ║īķĪ╣Õ╝ÅÕ«ÜńÉåÕ▒ĢÕ╝Ćõ║åŃĆ?br>ŃĆĆŃĆĆÕ£©ńē╣īDŖĶ«ĪµĢ░Õ║ÅÕłŚķćīķØóµÅÉÕłŅC║åńøÆĶŻģńÉāķŚ«ķóśŃĆéÕ░åpõĖ¬õĖŹÕÉīńÜäńÉāµöŠÕģźkõĖ¬ńøĖÕÉīńÜäńøÆÕŁÉÕQłµ»ÅõĖ¬ńøÆÕŁÉķØ×ĮI║’╝ēńÜäµ¢╣µ│ĢµĢ░µś»ń¼¼õ║īń▒╗StirlingµĢ░S(p, k)ÕQøÕ░åpõĖ¬ńøĖÕÉīńÜäńÉāµöŠÕģźkõĖ¬ńøĖÕÉīńÜäńøÆÕŁÉÕQłµ»ÅõĖ¬ńøÆÕŁÉķØ×ĮI║’╝ēńÜäµ¢╣µ│ĢµĢ░µś»ÕłåµŗåµĢ░ÕQīÕÅ»õ╗źÕĮÆŠlōõžōµĢ┤µĢ░ÕłÆÕłåķŚ«ķóśÕQīńö©ÕŖ©µĆüĶ¦äÕłÆµ▒éĶ¦Ż’╝ø׫åpõĖ¬õĖŹÕÉīńÜäńøÆÕŁÉµöæųģźõĖŹÕÉīńÜäkõĖ¬ńøÆÕŁÉÕŲłõĖöµ»ÅõĖ¬ķØ×ĮI║ńÜäµ¢ęÄ│ĢµĢŅCžōk! * S(p, k)ŃĆ?br>ŃĆĆŃĆƵ£ēÕćĀõĖ¬ÕŠłŠlÅÕģĖńÜäķĆƵĩÕģ│ń│╗ÕQܵ¢Éµ│óķéŻÕźæµĢ░ÕłŚŃĆüCatalanµĢÄ═╝łÕćĀń¦ŹŠlÅÕģĖńÜäÕ┼×Õ╝Å’╝ÜõĖēĶ¦ÆÕē¢ÕłåµĢ░ŃĆüõ║īÕÅēńö¤µłÉµĀæõĖ¬µĢ░ŃĆ?1-1Õ║ÅÕłŚŃĆüÕŖĀµŗ¼ÕÅĘÕ║ÅÕłŚĮ{ēńŁēÕQēŃĆüStirlingµĢÄ═╝łõĖżń¦ŹÕQīń¼¼õ║īń¦Źµ»öĶŠāÕĖĖńö©ÕQēŃĆüµ▒ēĶ»║ÕĪöŃĆünõĖ¬Õ£åÕłćÕē▓“q│ķØóµĢ░ŃĆünµØĪńø┤ŠU┐kõĖ¬õ║żńé╣ÕłćÕē▓ÕŃ^ķØóµĢ░Į{ēńŁēŃĆ鵣żÕż¢’╝īµĀŲDĄ\ÕŠäõĖŁµÅÉÕł░ńÜäÕŃ^┐UģRĆüÕÅŹ×«äÕÆīõĖĆõĖĆÕ»╣Õ║öśqÖõĖē┐UŹÕłåµ×ÉķŚ«ķóśńÜäµ¢ęÄ│Ģõ╣¤ÕŠłÕĆ╝ÕŠŚÕƤķē┤ŃĆ?br>
4.polyaÕ«ÜńÉå µ»öĶŠāÕżŹµØéÕQīĶ┐ćõĖĆķśĄÕŁÉÕźĮÕźĮµĆ╚Ø╗ōõĖŗŃĆ?img src ="http://www.shnenglu.com/sdfond/aggbug/81808.html" width = "1" height = "1" />
sdfond 2009-05-04 09:17 ÕÅæĶĪ©Ķ»äĶ«║
]]>sdfond 2009-04-30 09:12 ÕÅæĶĪ©Ķ»äĶ«║
]]>#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010;
struct Node
{
int v, id;
};
Node arr[N];
bool cmp(const Node &n1, const Node &n2)
{
return n1.v < n2.v;
}
int main()
{
int n, mine, cnt, pos, tol, ans, tmp, mini;
bool tag[N];
while (scanf("%d", &n) == 1)
{
mini = 0x3fffffff;
memset(tag, 0, sizeof(tag));
for (int i = 0; i < n; i++)
{
scanf("%d", &arr[i].v);
mini <?= arr[i].v;
arr[i].id = i;
}
sort(arr, arr + n, cmp);
ans = 0;
for (int i = 0; i < n; i++)
{
if (tag[i])
continue;
if (i == arr[i].id)
continue;
pos = i;
mine = arr[i].v;
cnt = 0;
tol = mine;
while (arr[pos].id != i)
{
cnt++;
pos = arr[pos].id;
tag[pos] = 1;
tol += arr[pos].v;
mine <?= arr[pos].v;
}
tmp = tol + (cnt - 1) * mine;
tmp <?= tol + mine + (cnt + 2) * mini;
ans += tmp;
}
printf("%d\n", ans);
}
return 0;
}
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010;
struct Node
{
int v, id;
};
Node arr[N];
bool cmp(const Node &n1, const Node &n2)
{
return n1.v < n2.v;
}
int main()
{
int n, mine, cnt, pos, tol, ans, tmp, mini;
bool tag[N];
while (scanf("%d", &n) == 1)
{
mini = 0x3fffffff;
memset(tag, 0, sizeof(tag));
for (int i = 0; i < n; i++)
{
scanf("%d", &arr[i].v);
mini <?= arr[i].v;
arr[i].id = i;
}
sort(arr, arr + n, cmp);
ans = 0;
for (int i = 0; i < n; i++)
{
if (tag[i])
continue;
if (i == arr[i].id)
continue;
pos = i;
mine = arr[i].v;
cnt = 0;
tol = mine;
while (arr[pos].id != i)
{
cnt++;
pos = arr[pos].id;
tag[pos] = 1;
tol += arr[pos].v;
mine <?= arr[pos].v;
}
tmp = tol + (cnt - 1) * mine;
tmp <?= tol + mine + (cnt + 2) * mini;
ans += tmp;
}
printf("%d\n", ans);
}
return 0;
}
sdfond 2009-04-17 09:05 ÕÅæĶĪ©Ķ»äĶ«║
]]>