n階常系數線性齊次遞推關系的解法有很多,特征方程法、生成函數法,但是對于編程最實用的是矩陣解法。
我們定義所要求的f(n) = Ak-1 * f(n - 1) + Ak-2 * f(n - 2) + ... + A0 * f(n-k),其中f(0)...f(k-1)的初值已經給好。
構造k * k的矩陣M:
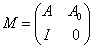
其中A =(Ak-1 Ak-2 ... A1),I是單位矩陣。
然后構造一個k * 1列向量b:

這樣,M * b之后b0的值就是f(k),以此類推,M ^ n * b之后b0的值就是f(k-1+n),算法復雜度O(k ^ 3 * logn)。
posted on 2009-05-08 22:08
sdfond 閱讀(511)
評論(0) 編輯 收藏 引用 所屬分類:
Algorithm - Combinatorics