紅黑樹的平衡
紅黑樹首先是一棵二叉查找樹,它每個結(jié)點都被標上了顏色(紅色或黑色),紅黑樹滿足以下5個性質(zhì):
1、 每個結(jié)點的顏色只能是紅色或黑色。
2、 根結(jié)點是黑色的。
3、 每個葉子結(jié)點都帶有兩個空的黑色結(jié)點(被稱為黑哨兵),如果一個結(jié)點n的只有一個左孩子,那么n的右孩子是一個黑哨兵;如果結(jié)點n只有一個右孩子,那么n的左孩子是一個黑哨兵。
4、 如果一個結(jié)點是紅的,則它的兩個兒子都是黑的。也就是說在一條路徑上不能出現(xiàn)相鄰的兩個紅色結(jié)點。
5、 對于每個結(jié)點來說,從該結(jié)點到其子孫葉結(jié)點的所有路徑上包含相同數(shù)目的黑結(jié)點。
紅黑樹的這5個性質(zhì)中,第3點是比較難理解的,但它卻非常有必要。我們看圖1中的左邊這張圖,如果不使用黑哨兵,它完全滿足紅黑樹性質(zhì),結(jié)點50到兩個葉結(jié)點8和葉結(jié)點82路徑上的黑色結(jié)點數(shù)都為2個。但如果加入黑哨兵后(如圖1右圖中的小黑圓點),葉結(jié)點的個數(shù)變?yōu)?/span>8個黑哨兵,根結(jié)點50到這8個葉結(jié)點路徑上的黑高度就不一樣了,所以它并不是一棵紅黑樹。
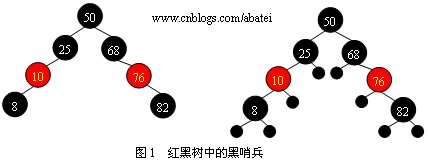
要看真正的紅黑樹請在以上動畫中添加幾個結(jié)點,看看是否滿足以上性質(zhì)。
紅黑樹的旋轉(zhuǎn)操作
紅黑樹的旋轉(zhuǎn)操作和AVL樹一樣,分為LL、RR、LR、RL四種旋轉(zhuǎn)類型,差別在于旋轉(zhuǎn)完成后改變的是結(jié)點的顏色,而不是平衡因子。旋轉(zhuǎn)動畫演示請參考AVL這篇文章中的Flash動畫:
http://www.cnblogs.com/abatei/archive/2008/11/17/1335031.html
紅黑樹上結(jié)點的插入
在討論紅黑樹的插入操作之前必須要明白,任何一個即將插入的新結(jié)點的初始顏色都為紅色。這一點很容易理解,因為插入黑點會增加某條路徑上黑結(jié)點的數(shù)目,從而導(dǎo)致整棵樹黑高度的不平衡。但如果新結(jié)點父結(jié)點為紅色時(如圖2所示),將會違返紅黑樹性質(zhì):一條路徑上不能出現(xiàn)相鄰的兩個紅色結(jié)點。這時就需要通過一系列操作來使紅黑樹保持平衡。

為了清楚地表示插入操作以下在結(jié)點中使用“新”字表示一個新插入的結(jié)點;使用“父”字表示新插入點的父結(jié)點;使用“叔”字表示“父”結(jié)點的兄弟結(jié)點;使用“祖”字表示“父”結(jié)點的父結(jié)點。插入操作分為以下幾種情況:
1、黑父
如圖3所示,如果新點的父結(jié)點為黑色結(jié)點,那么插入一個紅點將不會影響紅黑樹的平衡,此時插入操作完成。紅黑樹比AVL樹優(yōu)秀的地方之一在于黑父的情況比較常見,從而使紅黑樹需要旋轉(zhuǎn)的幾率相對AVL樹來說會少一些。
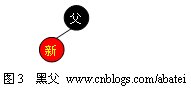
2.紅父
如果新點的父結(jié)點為紅色,這時就需要進行一系列操作以保證整棵樹紅黑性質(zhì)。如圖3所示,由于父結(jié)點為紅色,此時可以判定,祖父結(jié)點必定為黑色。這時需要根據(jù)叔父結(jié)點的顏色來決定做什么樣的操作。青色結(jié)點表示顏色未知。由于有可能需要根結(jié)點到新點的路徑上進行多次旋轉(zhuǎn)操作,而每次進行不平衡判斷的起始點(我們可將其視為新點)都不一樣。所以我們在此使用一個藍色箭頭指向這個起始點,并稱之為判定點。
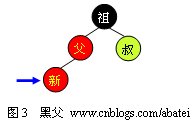
2.1 紅叔
當叔父結(jié)點為紅色時,如圖4所示,無需進行旋轉(zhuǎn)操作,只要將父和叔結(jié)點變?yōu)楹谏瑢⒆娓附Y(jié)點變?yōu)榧t色即可。但由于祖父結(jié)點的父結(jié)點有可能為紅色,從而違反紅黑樹性質(zhì)。此時必須將祖父結(jié)點作為新的判定點繼續(xù)向上進行平衡操作。
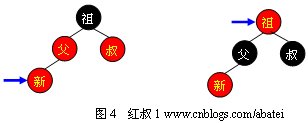
需要注意,無論“父”在“叔”的左邊還是右邊,無論“新”是“父”的左孩子還是右孩子,它們的操作都完全一樣。
2.2 黑叔
當叔父結(jié)點為黑色時,需要進行旋轉(zhuǎn),以下圖示了所有的旋轉(zhuǎn)可能
情形1:
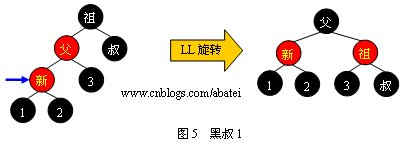
情形2:
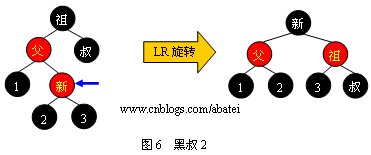
情形3:
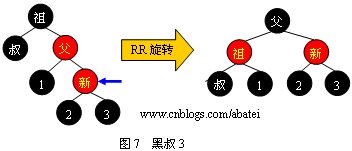
情形4:
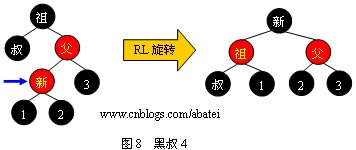
可以觀察到,當旋轉(zhuǎn)完成后,新的旋轉(zhuǎn)根全部為黑色,此時不需要再向上回溯進行平衡操作,插入操作完成。需要注意,上面四張圖的“叔”、“1”、“2”、“3”結(jié)點有可能為黑哨兵結(jié)點。
其實紅黑樹的插入操作不是很難,甚至比AVL樹的插入操作還更簡單些。但刪除操作就遠遠比AVL樹復(fù)雜得多,下面就介紹紅黑樹的刪除操作。
紅黑樹上結(jié)點的刪除
紅黑樹本身是一棵二叉查找樹,它的刪除和二叉查找樹的刪除類似。首先要找到真正的刪除點,當被刪除結(jié)點n存在左右孩子時,真正的刪除點應(yīng)該是n的中序遍在前驅(qū),關(guān)于這一點請復(fù)習(xí)二叉查找樹的刪除。如圖9所示,當刪除結(jié)點20時,實際被刪除的結(jié)點應(yīng)該為18,結(jié)點20的數(shù)據(jù)變?yōu)?/span>18。
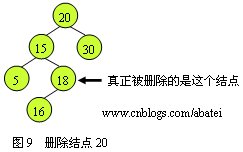
所以可以推斷出,在進行刪除操作時,真正的刪除點必定是只有一個孩子或沒有孩子的結(jié)點。而根據(jù)紅黑樹的性質(zhì)可以得出以下兩個結(jié)論:
1、 刪除操作中真正被刪除的必定是只有一個紅色孩子或沒有孩子的結(jié)點。
2、 如果真正的刪除點是一個紅色結(jié)點,那么它必定是一個葉子結(jié)點。
理解這兩點非常重要,如圖10所示,除了情況(a)外,其他任一種況結(jié)點N都無法滿足紅黑樹性質(zhì)。
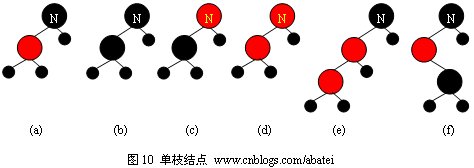
在以下討論中,我們使用藍色箭頭表示真正的刪除點,它也是旋轉(zhuǎn)操作過程中的第一個判定點;真正的刪除點使用“舊”標注,舊點所在位置將被它的的孩子結(jié)點所取代(最多只有一個孩子),我們使用“新”表示舊點的孩子結(jié)點。刪除操作可分為以下幾種情形:
1、舊點為紅色結(jié)點
若舊點為紅色結(jié)點,則它必定是葉子結(jié)點,直接刪除即可。如圖11所示
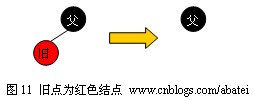
2、一紅一黑
當舊點為黑色結(jié)點,新點為紅色結(jié)點時,將新點取代舊點位置后,將新點染成黑色即可(如圖12所示)。這里需要注意:舊點為紅色,新點為黑色的情況不可能存在。
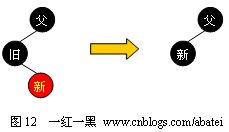
3、雙黑
當舊點和新點都為黑色時(新點為空結(jié)點時,亦屬于這種情況),情況比較復(fù)雜,需要根據(jù)舊點兄弟結(jié)點的顏色來決定進行什么樣的操作。我們使用“兄”來表示舊點的兄弟結(jié)點。這里可分為紅兄和黑兄兩種情況:
3.1 紅兄
由于兄弟結(jié)點為紅色,所以父結(jié)點必定為黑色,而舊點被刪除后,新點取代了它的位置。下圖演示了兩種可能的情況:
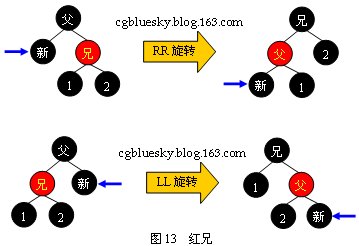
紅兄的情況需要進行RR或LL型旋轉(zhuǎn),然后將父結(jié)點染成紅色,兄結(jié)點染成黑色。然后重新以新點為判定點進行平衡操作。我們可以觀察到,旋轉(zhuǎn)操作完成后,判定點沒有向上回溯,而是降低了一層,此時變成了黑兄的情況。
3.2 黑兄
黑兄的情況最為復(fù)雜,需要根據(jù)黑兄孩子結(jié)點(這里用“侄”表示)和父親結(jié)點的顏色來決定做什么樣的操作。
3.2.1 黑兄二黑侄紅父
如圖14所示,這種情況比較簡單,只需將父結(jié)點變?yōu)楹谏纸Y(jié)點變?yōu)楹谏陆Y(jié)點變?yōu)楹谏纯桑瑒h除操作到此結(jié)束。
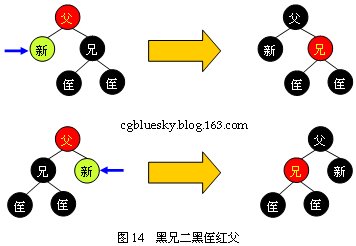
3.2.2 黑兄二黑侄黑父
如圖15所示,此時將父結(jié)點染成新結(jié)點的顏色,新結(jié)點染成黑色,兄結(jié)點染成紅色即可。當新結(jié)點為紅色時,父結(jié)點被染成紅色,此時需要以父結(jié)點為判定點繼續(xù)向上進行平衡操作。
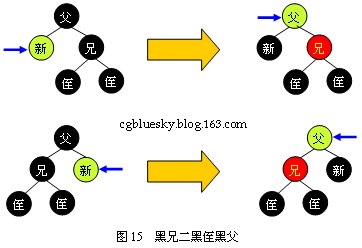
3.2.3 黑兄紅侄
黑兄紅侄有以下四種情形,下面分別進行圖示:
情形1:
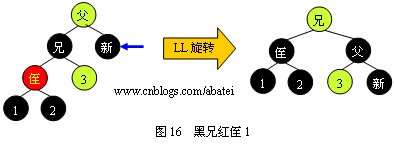
情形2:
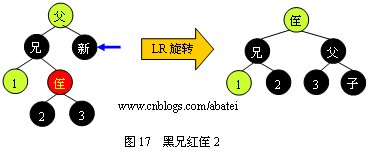
情形3:

情形4:
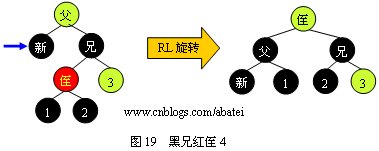
由以上圖例所示,看完以上四張圖的兄弟有可能會有一個疑問,如果情形1和情形2中的兩個侄子結(jié)點都為紅色時,是該進行LL旋轉(zhuǎn)還是進行LR旋轉(zhuǎn)呢?答案是進行LL旋轉(zhuǎn)。情形3和情形4則是優(yōu)先進行RR旋轉(zhuǎn)的判定。
紅黑樹的代碼實現(xiàn)