問題一：求N個點中斜率最大的兩個點。
要解決該問題，我們首先證明一個結(jié)論：三個點a、b、c，若x_a < x_b < x_c則斜率最大者必定是ab或者是bc，而不會是ac。證明如下：
我們用k表示斜率，
不妨假設k_ac > k_ab，即(y_c - y_a)/(x_c - x_a) - (y_b - y_a)/(x_b - x_a) > 0
則可以推出x_a * y_b + x_b * y_c + x_c * y_a > x_a * y_c + x_b * y_a + x_c * y_b
那么可以得出k_bc - k_ac = (y_c - y_b)/(x_c - x_b) - (y_c - y_a)/(x_c - x_a)  = (x_a * y_b + x_b * y_c + x_c * y_a) - (x_a * y_c + x_b * y_a + x_c * y_b) > 0
所以可以知道如果ac斜率大于ab，那么它就不可能大于bc
同理可以得出若ac斜率大于bc，那么它就不可能大于ab
證畢。
有了上面的證明，我們就可以先對N個點的橫坐標排序，然后再計算a[i]與a[i + 1]的斜率，取最大值即可。
代碼略。

問題二：求N個點中距離最遠的兩點距離。
典型的求凸包直徑問題，這里先講解一下如何利用Graham scanning方法在O(nlogn)時間內(nèi)求凸包，然后利用旋轉(zhuǎn)卡殼法在O(n)時間內(nèi)求凸包直徑。
該問題面試中一般不會問到，太過復雜，不過應該學習這種思想。
1）Graham scanning求凸包：
首先：選取N個點中y坐標最小的點為P₀，若有多個點y坐標相同，則取x坐標最小的點為P₀，即P₀為坐標系中左下角的點。
然后：根據(jù)direction(P₀, P_i, P_j)來排序，direction()函數(shù)是求P₀P_i向量和P₀P_j向量的叉積，叉積的作用是判定P₀P_i向量在P₀P_j向量的逆時針方向還是順時針方向，如果P₀P_i X P₀P_j > 0則說明P₀P_i在P₀P_j的順時針方向，否則在逆時針方向。另外叉積的值的絕對值還表示以P₀P_iP_j三點組成的三角形的面積，因為P₀P_i X P₀P_j = |P₀P_i| * |P₀P_j| * sin∠P_iP₀P_j，這個結(jié)論會在卡殼時用到。有了上面的知識，可以知道排序后的結(jié)果是所有節(jié)點圍繞P₀以逆時針方向排列。
再次：將點P₀和點P₁入棧，然后從P₂到P_n循環(huán)執(zhí)行下面操作：若direction(P_{stack[top - 1]}, P_stack[top], P_i) < 0，則刪除棧頂元素，即top--（因為排序的時候，如果兩個節(jié)點對P₀的向量叉積若相等，則距離P₀遠的節(jié)點排在后面，所以這里如果上述等式等于0的話則可以肯定P_i到P_{stack[top - 1]}的距離比P_stack[top]到P_{stack[top - 1]}的距離遠，所以可以直接將P_stack[top]出棧，當然也可以不出棧，因為某個在凸包多邊形的某條邊上的點，可以算作凸包的點，也可以去掉），否則P_i進棧。直到P_n判斷完畢。
最后：棧stack中的所有點就是凸包多邊形的點，并且從棧底到棧頂以逆時針排列。
上面算法表述的比較羅嗦，看下面的圖示就明白了：
首先是排序，然后是P₀和P₁入棧：



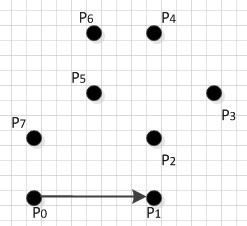
然后是判斷P₂是否應該入棧：



因為P₀P₁ X P₀P₂ > 0，所以P₂入棧：



然后判斷P₃是否應該入棧：



因為P₁P₂ X P₁P₃ < 0，所以P₂出棧P₃入棧：



判斷P₄是否應該入棧：



因為P₁P₃ X P₁P₄ > 0，所以P₄入棧：



判斷P₅是否應該入棧：



因為P₃P₄ X P₃P₅ > 0，所以P₅入棧：



判斷P₆是否應該入棧：



因為P₄P₅ X P₄P₆ < 0，所以p₅出棧P₆入棧：



最后p7入棧，形成最終的凸包：



通過以上圖示過程可以清晰明白凸包的構(gòu)建過程。證明過程比較復雜，詳見《算法導論》。