欧美交受高潮1,蜜桃av噜噜一区,av成人毛片

LLawliet — Tue, 25 Oct 2011 15:52:00 GMT

1043: Atlantis

Result	TIME Limit	MEMORY Limit	Run Times	AC Times	JUDGE
	3s	8192K	431	155	Standard

There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.

Input

The input file consists of several test cases. Each test case starts with a line containing a single integer n(1 < n < 100) of available maps. The n following lines describe one map each. Each of these lines containsfour numbers x1;y1;x2;y2 (0 < x1 < x2 < 100000;0 < y1 < y2 < 100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.The input file is terminated by a line containing a single 0. Don’t process it1.

Output

For each test case, your program should output one section. The first line of each section must be “Testcase #k”, where k is the number of the test case (starting with 1). The second one must be “Total explored area: a”, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.

Output a blank line after each test case.

Sample Input

2
10 10 20 20
15 15 25 25.5
0

Sample Output

Test case #1
Total explored area: 180.00

题目的意思是�l�定n个矩形的2n个坐标，求矩形的覆盖面积。如果开一个大的bool数组�Q�将覆盖�q�的部分更新为true�Q�再从头到尾扫描一遍，在坐标范围比较小的情况下�Q�可以求解。但是如果坐标x,y的取��D��围很大，比如[-10^8,10^8]�Q�用上面�q�个�Ҏ��׃��能求解了�Q�而且坐标�q�有可能是实敎ͼ�上面的方法就更加不可行了�Q�需要寻找一�U�新的解法，��是下面要说到的“��L��?#8221;�?br /> 注意到要表示一个矩形，只需要知道其2个顶点的坐标��可以了(最左下�Q�最右上)。可以用2个数�l�x[0...2n-1]�Q�y[0...2n-1]记录下矩形Ri�?个坐�?x1,y1)�Q?x2,y2)�Q�然后将数组x[0...xn-1]�Q�y[0...2n-1]排序�Q��ؓ下一步的扫描�U�作准备�Q�这��是��L��化的思想。这题还可以用线�D�|��做进一步优化，但是�q�里只介�l�离散化的思想�?br /> 看下面这个例子：�?个矩�?1,1)�Q?3,3)�?2,2)�Q?4,4)。如图：

    图中虚线表示扫描�U�，下一步工作只需要将�q?个矩形覆盖过的部分的bool数组的对应位�|�更��Cؓtrue�Q�接下去用扫描线从左到右�Q�从上到下扫描一遍，��可以求出矩形覆盖的总面�U��?br />    �q�个囑֯�应的bool数组的值如下：
    1 1 0                       1 2 3
    1 1 1       <---->       4 5 6
    0 1 1                       7 8 9

代码�Q?/div>

#include<stdio.h>
#include<iostream>
#include<algorithm>
#define MAXN 201
using namespace std;

struct Node
{
    int l, r;//�U�段树的左右整点
    int c;//c用来记录重叠情况
    double cnt, lf, rf;//
    //cnt用来计算实在的长度，rf,lf分别是对应的左右真实的��Q�Ҏ��端点
} segTree[MAXN * 3];
struct Line
{
    double x, y1, y2;
    int f;
} line[MAXN];
//把一�D�|��q��于y轴的�U�段表示成数�l?nbsp;�Q?br />//x是线�D늚�x坐标�Q�y1,y2�U�段对应的下端点和上端点的坐�?br />//一个矩�?nbsp;�Q�左边的那条边f�?�Q�右边的�?1�Q?br />//用来记录重叠情况�Q�可以根据这个来计算�Q�nod节点中的c

bool cmp(Line a,Line b)//sort排序的函�?/span>
{
    return a.x < b.x;
}

double y[MAXN];//记录y坐标的数�l?/span>
void Build(int t,int l,int r)//构造线�D�|��
{
    segTree[t].l = l;
    segTree[t].r = r;
    segTree[t].cnt = segTree[t].c = 0;
    segTree[t].lf = y[l];
    segTree[t].rf = y[r];
    if (l + 1 == r) return;
    int mid = (l + r) >> 1;
    Build(t << 1, l, mid);
    Build(t << 1 | 1, mid, r);//递归构�?/span>
}
void calen(int t)//计算长度
{
    if (segTree[t].c > 0)
    {
        segTree[t].cnt = segTree[t].rf - segTree[t].lf;
        return;
    }
    if (segTree[t].l + 1 == segTree[t].r)
        segTree[t].cnt = 0;
    else
        segTree[t].cnt = segTree[t << 1].cnt + segTree[t << 1 | 1].cnt;
}
void update(int t, Line e)//加入�U�段e�Q�后更新�U�段�?/span>
{
    if (e.y1 == segTree[t].lf && e.y2 == segTree[t].rf)
    {
        segTree[t].c += e.f;
        calen(t);
        return;
    }
    if (e.y2 <= segTree[t << 1].rf)
        update(t << 1, e);
    else
    if(e.y1 >= segTree[t << 1 | 1].lf)
        update(t << 1 | 1, e);
    else
    {
        Line tmp = e;
        tmp.y2 = segTree[t << 1].rf;
        update(t << 1, tmp);
        tmp = e;
        tmp.y1 = segTree[t << 1 | 1].lf;
        update(t << 1 | 1, tmp);
    }
    calen(t);
}
int main()
{
    int i, n, t, iCase = 0;
    double x1, y1, x2, y2;
    while(scanf("%d", &n) && n)
    {
        iCase++;
        t = 1;
        for(i = 1; i <= n; i++)
        {
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            line[t].x = x1;
            line[t].y1 = y1;
            line[t].y2 = y2;
            line[t].f = 1;
            y[t] = y1;
            t++;
            line[t].x = x2;
            line[t].y1 = y1;
            line[t].y2 = y2;
            line[t].f = -1;
            y[t] = y2;
            t++;
        }
        sort(line + 1, line + t, cmp);
        sort(y + 1, y + t);
        Build(1, 1, t - 1);
        update(1, line[1]);
        double res = 0;
        for(i = 2; i < t; i++)
        {
            res += segTree[1].cnt * (line[i].x - line[i - 1].x);
            update(1, line[i]);
        }
        printf("Test case #%d\n", iCase);
        printf("Total explored area: %.2lf\n\n", res);
    }
    return 0;
}

LLawliet 2011-10-25 23:52 发表评论

LLawliet — Tue, 25 Oct 2011 12:55:00 GMT

We can number binary trees using the following scheme:

The empty tree is numbered 0.
The single-node tree is numbered 1.
All binary trees having m nodes have numbers less than all those having m+1 nodes.
Any binary tree having m nodes with left and right subtrees L and R is numbered n such that all trees having m nodes numbered > n have either

Left subtrees numbered higher than L, or
A left subtree = L and a right subtree numbered higher than R.

The first 10 binary trees and tree number 20 in this sequence are shown below:

Your job for this problem is to output a binary tree when given its order number.

Input

Input consists of multiple problem instances. Each instance consists of a single integer n, where 1 <= n <= 500,000,000. A value of n = 0 terminates input. (Note that this means you will never have to output the empty tree.)

Output

For each problem instance, you should output one line containing the tree corresponding to the order number for that instance. To print out the tree, use the following scheme:

A tree with no children should be output as X.
A tree with left and right subtrees L and R should be output as (L')X(R'), where L' and R' are the representations of L and R.
If L is empty, just output X(R').
If R is empty, just output (L')X.

Sample Input

Sample Output

X 
((X)X(X))X
(X(X(((X(X))X(X))X(X))))X(((X((X)X((X)X)))X)X)

思�\�Q?br />a数组表示节点��Cؓj所能表�C�最大的数�?br />则第j个节�Ҏ��能表�C�的数a[j]�W�合卡特兰数�Q?br />a[j] = a[0] * a[j - 1] + a[1] * a[j - 2] + ...... + a[j - 1] * a[0];
表示�Q�有j个节�?= 左边0个节点的个数 * 双��j - 1个节点的个数 + ...... + 左边j - 1个节点的个数 * 双��0个节点的个数�?br />
之后�Ҏ��d��的n�Q�判断出节点敎ͼ�在再判断出左右的节点数和左右所代表的数�?br />然后调用递归�?br />

#include <cstdio>
#include <cstring>
using namespace std;

int a[25], b[25];

void solve(int n)
{
    int t, i, j;
    if (n == 0) return;
    if (n == 1)
    {
        printf("X");
        return;
    }
    for (j = 1;; ++j)
    {
        if (b[j] >= n)
            break;
    }
    n = n - b[j - 1];
    for (i = 0; i < j; ++i)
    {
        t = a[i] * a[j - 1 - i];
        if (n > t)
        {
            n = n - t;
        }
        else
            break;
    }
    if (i != 0)
    {
        printf("(");
        solve(b[i - 1] + 1 + (n - 1)/ a[j - 1 - i]);
        printf(")");
    }
    printf("X");
    if (i != j - 1)
    {
        printf("(");
        solve(b[j - 2 - i] + 1 + (n - 1) % a[j - 1 - i]);
        printf(")");
    }
}

int main()
{
    int n;
    int i, j;
    b[0] = 0;
    a[0] = b[1] = a[1] = 1;
    for (i = 2; i < 20; ++i)
    {
        a[i] = 0;
        for (j = 0; j < i; ++j)
        {
            a[i] += a[j] * a[i - j - 1];
        }
        b[i] = b[i - 1] + a[i];
    }
    while (scanf("%d", &n) && n)
    {
        solve(n);
        printf("\n");
    }
    return 0;
}

LLawliet 2011-10-25 20:55 发表评论

JOJ1037�Q�Operand

LLawliet — Tue, 25 Oct 2011 11:53:00 GMT

Professor Maple teaches mathematics in a university. He have invented a function for the purpose of obtaining the operands from an expression. The function named op(i,e) can be described as follows: The expression e may be divided into sub-expression(s) by the operator, which has the lowest priority in the expression. For example, the expression “a*b+b*c+c*d” should be divided into three sub-expressions “a*b”, “b*c” and “c*d”, because the operator “+” has the lowest priority. The purpose of this function is to extract the ith sub-expression as the result. So, in the example above, op(2,e)=b*c.

If we regard the sub-expression as the main expression, it might be divided again and again. Obviously, the dividing process is recursive. As you see, the following example is much more complex:

Let p:=a^b*c+(d*c)^f*z+b
op(1,op(1,op(2,p)))=(d*c)
op(1,op(1,op(1,op(2,p))))=d*c
op(2,op(2,p))=z
op(3,p)=b
op(1,op(3,p))=b

Professor Maple is so lazy that he would leave the work to computer rather than do it himself, when the expression is long and complicated. Of course, without your program, the computer won’t work out the result automatically.

Input

The input file contains several test cases. The last test case in the input file is followed by a line containing a symbol “*”, indicating the end of the input data. Each test case consists of two parts. The first part describes the expression, while the second part contains several questions, which should be calculated according to the expression.

The first line of each test case contains an expression consists of the expression name, “:=” and the content of the expression. The expression name is a lowercase. And the content is composed by lowercases and operators “+”, “(”, “)”, “*” and “^”. For example, here is a valid expression, p:=a^b*c+(d*c)^f*z+b. Among those operators, “(” and “)” have the highest priority. The operator “^” has a lower priority, and then “*”. The priority of the operator “+” is the lowest.

The second line of each test case contains an integer n indicating n questions based on the above expression. This is followed by n lines. Each of them contains the description of one question, which consists of integers. For example, the question with three integers “2 1 1” describes the function op(1,op(1,op(2,e))). To compute this function, we have to keep to the following sequence: First, according to the first integer 2, divide the expression and extract the 2nd sub-expression. Then, according to the second integer 1, divide the sub-expression and extract the 1st one. Finally, according to the third integer 1, divide the outcome again, and extract the result.

Output

For each test case, display the expression name and a colon on the first line. Then display the result of each question on a line. The layout of the output is shown in the sample output.

You may assume that all expressions and functions are always valid.

Display a blank line between test cases.

Sample Input

p:=a^b*c+(d*c)^f*z+b 
4 
2 1 1 
2 2 
3 
3 1 
a:=(x+y) 
3 
1 
1 2 
1 2 1 
*

Sample Output

Expression p: 
op(1,op(1,op(2,p)))=(d*c) 
op(2,op(2,p))=z 
op(3,p)=b 
op(1,op(3,p))=b  

Expression a: 
op(1,a)=x+y 
op(2,op(1,a))=y 
op(1,op(2,op(1,a)))=y

模拟题，处理好原字符串的优先�U�就行了�?br />代码�Q?br />

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;

int find(char c)
{
    if (c == '(' || c == ')') return 4;
    if (c == '^') return 3;
    if (c == '*') return 2;
    if (c == '+') return 1;
    return 1000;
}

char s[101];
string e;
int n, i, j, k, p[101], r[101], v[101], head, tail, x, ri, d = 0;

int main()
{
    while (scanf("%s", s), s[0] != '*')
    {
        if (d++) puts("");
        head = 0;
        e = "";
        while (s[head] != ':')
          e += s[head++];
        head += 2;
        printf("Expression %s:\n", e.c_str());
        tail = strlen(s) - 1;
        x = 0;
        for (i = head; i <= tail; ++i)
        {
            if (s[i] == ')') x -= 4;
            v[i] = find(s[i]) + x;
            if (s[i] == '(') x += 4;
        }
        scanf("%d\n", &k);
        for (i = 0; i < k; ++i)
        {
            ri = 0;
            int head1 = 3, min1, t;
            tail = strlen(s);
            char c;
            while ((c = getchar()) != '\n')
            {
                cin.putback(c);
                scanf("%d", &n);
                r[ri++] = n;
                min1 = 1000;
                for (j = head1; j < tail; ++j)
                  if (v[j] < min1) min1 = v[j];
                if (s[head1] == '(' && s[tail - 1] == ')' && min1 == v[head1])
                {
                    head1++;
                    tail--;
                }
                else
                  if (head1 + 1 == tail){}
                else
                {
                    p[0] = head1 - 1;
                    for (j = head1, t = 1; j < tail; ++j)
                      if (v[j] == min1)
                      {
                          p[t++] = j;
                      }
                    p[t] = tail;
                    head1 = p[n - 1] + 1;
                    tail = p[n];
                }
            }
            for (j = ri - 1; j >= 0; --j)
              printf("op(%d,", r[j]);
            printf("%s", e.c_str());
            for (j = 0; j < ri; ++j)
              printf(")");
            printf("=");
            for (j = head1; j < tail; ++j)
                printf("%c", s[j]);
            puts("");
        }
    }
    return 0;
}

LLawliet 2011-10-25 19:53 发表评论

POJ1679:The Unique MST

LLawliet — Mon, 17 Oct 2011 13:07:00 GMT

The Unique MST

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 11943		Accepted: 4112

Description

Given a connected undirected graph, tell if its minimum spanning tree is unique.

Definition 1 (Spanning Tree): Consider a connected, undirected graph G = (V, E). A spanning tree of G is a subgraph of G, say T = (V', E'), with the following properties:
1. V' = V.
2. T is connected and acyclic.

Definition 2 (Minimum Spanning Tree): Consider an edge-weighted, connected, undirected graph G = (V, E). The minimum spanning tree T = (V, E') of G is the spanning tree that has the smallest total cost. The total cost of T means the sum of the weights on all the edges in E'.

Input

The first line contains a single integer t (1 <= t <= 20), the number of test cases. Each case represents a graph. It begins with a line containing two integers n and m (1 <= n <= 100), the number of nodes and edges. Each of the following m lines contains a triple (xi, yi, wi), indicating that xi and yi are connected by an edge with weight = wi. For any two nodes, there is at most one edge connecting them.

Output

For each input, if the MST is unique, print the total cost of it, or otherwise print the string 'Not Unique!'.

Sample Input

Sample Output

3 
Not Unique!

Source

POJ Monthly--2004.06.27 srbga@P

代码�Q?br />

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

typedef struct
{
    int x, y, w;
} edge;

edge s[10010];
int top, t[10010];

bool cmp(edge a, edge b)
{
    return a.w < b.w;
}

int kru(int n, int m, int x)
{
    int i, j, a, b, tag[110], tem, sum, k;
    for (i = 0; i < n; ++i)
    {
        tag[i] = i;
    }
    k = 1, j = 0, sum = 0;
    while (k < n)
    {
        a = s[j].x - 1;
        b = s[j].y - 1;
        if (j == x)
        {
            j++;
            continue;
        }
        if (tag[a] != tag[b])
        {
            if (x == -1)
            {
                t[top] = j;
                top++;
            }
            tem = tag[b];
            k++, sum += s[j].w;
            for (i =  0; i < n; ++i)
            {
                if (tag[i] == tem)
                {
                    tag[i] = tag[a];
                }
            }
        }
        j++;
    }
    return sum;
}
int main()
{
    int p, n, m, cmin;
    scanf("%d", &p);
    while (p--)
    {
        int flag = 1;
        scanf("%d%d", &n, &m);
        for (int i = 0; i < m; ++i)
            scanf("%d%d%d", &s[i].x, &s[i].y, &s[i].w);
        sort(s, s + m, cmp);
        top = 0;
        int min = kru(n, m, -1);
        int key = top;
        for (int l = 0; l < key; ++l)
        {
            cmin = kru(n, m, t[l]);
            if (cmin == min)
            {
                flag = 0;
                printf("Not Unique!\n");
                break;
            }
        }
        if (flag)
        printf("%d\n", min);
    }
    return 0;
}

LLawliet 2011-10-17 21:07 发表评论

POJ3463�Q�Sightseeing

LLawliet — Mon, 17 Oct 2011 08:30:00 GMT

Sightseeing

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 4917		Accepted: 1688

Description

Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights.

Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.

There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.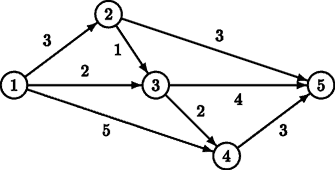

For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.

Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.

Input

The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:

One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.
M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.
The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.
One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.
There will be at least one route from S to F.

Output

For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 10⁹ = 1,000,000,000.

Sample Input

Sample Output

3
2

Hint

The first test case above corresponds to the picture in the problem description.

Source

BAPC 2006 Qualification

思�\:

依据描写可知�Q�本题的要求即便要求出最短�\和比最短�\�?的次短�\�Q�因而可用Dijkstra来处理。翔实做法如下：用两�l�数��d��登记最短�\和次短�\的长度（dist�Q�，条数�Q�cnt�Q�，拜会�W�号�Q�used�Q�，��Z��个优先队列，元素单位包括节点序号�Q�v�Q�，该节点�\�l�长�Q�len�Q�，以及登记路径�U�类�Q�ref�Q�，每次从优先队列中取出��用节点后，用它所登记的�\径长更新待比拟�\径，��d��用它和目前所登记的该节点的最短�\径以及此�D��\径比拟，中意更新条�g则登记�\径种�c�，�q�生成新节点加入优先队列�Q�同时更新目前节点处该种�c��\径条数。万一不中意条件然而中意�؜同联�p�，则增加相应的条数到该节点所登记的�\径条��C��?/span>

代码�Q?br />

#include <cstdio>
#include <memory.h>
#include <queue>
#define N 1001
#define M 10001
#define INF 0x7fffffff
#define clr(a) memset(a, 0, sizeof(a))
using namespace std;

struct Edge
{
    int v, len, ref;
    Edge *link;
    Edge new_E(int v1, int l, int r)
    {
        v = v1, len = l, ref = r;
        return *this;
    }
} *E[N], mempool[M];

int dist[N][2], used[N][2], cnt[N][2];
int n, m, memh, S, T;

void AddEdge(int u, int v, int len)
{
    Edge *e = &mempool[memh++];
    e -> v = v;
    e -> len = len;
    e -> link = E[u];
    E[u] = e;
}

bool operator < (Edge a, Edge b)
{
    return a.len > b.len;
}

priority_queue <Edge, vector <Edge> > Q;

void InitData()
{
    int i, u, v, len;
    memh = 0;
    scanf("%d%d", &n, &m);
    clr(E);
    for (i = 1; i <= m; ++i)
    {
        scanf("%d%d%d", &u, &v, &len);
        AddEdge(u, v, len);
    }
    scanf("%d%d", &S, &T);
}

int Dijstra()
{
    Edge D, P;
    clr(cnt);
    clr(used);
    for (int i = 1; i <= n; ++i)
        dist[i][0] = dist[i][1] = INF;
    dist[S][0] = 0;
    cnt[S][0] = 1;
    while (!Q.empty())
        Q.pop();
    Q.push(D.new_E(S, 0, 0));
    while (!Q.empty())
    {
        P = Q.top();
        Q.pop();
        if (!used[P.v][P.ref])
        {
            used[P.v][P.ref] = 1;
            for (Edge *e = E[P.v]; e; e = e -> link)
            {
                int tmp = P.len + e -> len;
                if (tmp < dist[e -> v][0])
                {
                    if (dist[e -> v][0] != INF)
                    {
                        dist[e -> v][1] = dist[e -> v][0];
                        cnt[e -> v][1] = cnt[e -> v][0];
                        Q.push(D.new_E(e -> v, dist[e -> v][0], 1));
                    }
                    dist[e -> v][0] = tmp;
                    cnt[e -> v][0] = cnt[P.v][P.ref];
                    Q.push(D.new_E(e -> v, tmp, 0));
                }
                else
                if (tmp == dist[e -> v][0])
                {
                    cnt[e -> v][0] += cnt[P.v][P.ref];
                }
                else
                if (tmp < dist[e -> v][1])
                {
                    dist[e -> v][1] = tmp;
                    cnt[e -> v][1] = cnt[P.v][P.ref];
                    Q.push(D.new_E(e -> v, tmp, 1));
                }
                else
                if (dist[e -> v][1] == tmp)
                {
                    cnt[e -> v][1] += cnt[P.v][P.ref];
                }
            }
        }
    }
    if (dist[T][1] - 1 == dist[T][0])
        cnt[T][0] += cnt[T][1];
    return cnt[T][0];
}

int main()
{
    int T;
    scanf("%d", &T);
    while (T--)
    {
        InitData();
        printf("%d\n", Dijstra());
    }
}

LLawliet 2011-10-17 16:30 发表评论

POJ3522:Slim Span

LLawliet — Mon, 17 Oct 2011 07:54:00 GMT

Slim Span

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 4023		Accepted: 2116

Description

Given an undirected weighted graph G, you should find one of spanning trees specified as follows.

The graph G is an ordered pair (V, E), where V is a set of vertices {v₁, v₂, …, v_n} and E is a set of undirected edges {e₁, e₂, …, e_m}. Each edge e ∈ E has its weight w(e).

A spanning tree T is a tree (a connected subgraph without cycles) which connects all the n vertices with n − 1 edges. The slimness of a spanning tree T is defined as the difference between the largest weight and the smallest weight among the n − 1 edges of T.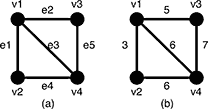

Figure 5: A graph G and the weights of the edges

For example, a graph G in Figure 5(a) has four vertices {v₁, v₂, v₃, v₄} and five undirected edges {e₁, e₂, e₃, e₄, e₅}. The weights of the edges are w(e₁) = 3, w(e₂) = 5, w(e₃) = 6, w(e₄) = 6, w(e₅) = 7 as shown in Figure 5(b).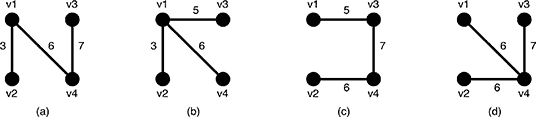

Figure 6: Examples of the spanning trees of G

There are several spanning trees for G. Four of them are depicted in Figure 6(a)~(d). The spanning tree T_a in Figure 6(a) has three edges whose weights are 3, 6 and 7. The largest weight is 7 and the smallest weight is 3 so that the slimness of the tree T_a is 4. The slimnesses of spanning trees T_b, T_c and T_d shown in Figure 6(b), (c) and (d) are 3, 2 and 1, respectively. You can easily see the slimness of any other spanning tree is greater than or equal to 1, thus the spanning tree Td in Figure 6(d) is one of the slimmest spanning trees whose slimness is 1.

Your job is to write a program that computes the smallest slimness.

Input

The input consists of multiple datasets, followed by a line containing two zeros separated by a space. Each dataset has the following format.

n	m
a₁	b₁	w₁
	⋮
a_m	b_m	w_m

Every input item in a dataset is a non-negative integer. Items in a line are separated by a space. n is the number of the vertices and m the number of the edges. You can assume 2 ≤ n ≤ 100 and 0 ≤ m ≤ n(n − 1)/2. a_k and b_k (k = 1, …, m) are positive integers less than or equal to n, which represent the two vertices v_{a_k} and v_{b_k} connected by the kth edge e_k. w_k is a positive integer less than or equal to 10000, which indicates the weight of e_k. You can assume that the graph G = (V, E) is simple, that is, there are no self-loops (that connect the same vertex) nor parallel edges (that are two or more edges whose both ends are the same two vertices).

Output

For each dataset, if the graph has spanning trees, the smallest slimness among them should be printed. Otherwise, −1 should be printed. An output should not contain extra characters.

Sample Input

Sample Output

Source

Japan 2007

题目��是生成一��|��Q�要求边权最大减最��的差最��?br />�Ҏ��Kruskal思想�Q�把�Ҏ��序，之后枚�D一下就行了�?br />
代码�Q?br />

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int M = 5005;
const int INF = 1 << 29;

struct edge
{
    int st, ed, w;
    bool operator < (edge a) const
    {
        return w < a.w;
    }
} e[M];

int n, m, ans, num, temp;
int f[105], rank[105];

void makeset()
{
    for (int i = 1; i <= n; ++i)
        f[i] = i;
    memset(rank, 0, sizeof(rank));
}

int find(int x)
{
    while (f[x] != x) x = f[x];
    return x;
}

void unionset(int a, int b)
{
    int p = find(a);
    int q = find(b);
    if (rank[p] > rank[q])
        f[q] = p;
    else
    if (rank[p] < rank[q])
        f[p] = q;
    else
    {
        f[p] = q;
        rank[q]++;
    }
}

void kruskal()
{
    ans = INF;
    for (int i = 0; i < m - n + 2; ++i)
    {
        makeset();
        temp = -1;
        num = 0;
        for (int j = i; j < m; ++j)
        {
            if (find(e[j].st) != find(e[j].ed))
            {
                num++;
                unionset(e[j].st, e[j].ed);
                if (num == n - 1)
                {
                    temp = e[j].w - e[i].w;
                    break;
                }
            }
        }
        if (temp == -1) break;
        if (temp != -1 && temp < ans) ans = temp;
    }
    if (ans >= INF) printf("-1\n");
    else printf("%d\n", ans);
}

int main()
{
    while (scanf("%d%d", &n, &m), n || m)
    {
        for (int i = 0; i < m; ++i)
            scanf("%d%d%d", &e[i].st, &e[i].ed, &e[i].w);
        sort(e, e + m);
        kruskal();
    }
    return 0;
}

LLawliet 2011-10-17 15:54 发表评论

POJ2449�Q�Remmarguts' Date

LLawliet — Mon, 17 Oct 2011 07:19:00 GMT

Remmarguts' Date

Time Limit: 4000MS		Memory Limit: 65536K
Total Submissions: 12450		Accepted: 3422

Description

"Good man never makes girls wait or breaks an appointment!" said the mandarin duck father. Softly touching his little ducks' head, he told them a story.

"Prince Remmarguts lives in his kingdom UDF – United Delta of Freedom. One day their neighboring country sent them Princess Uyuw on a diplomatic mission."

"Erenow, the princess sent Remmarguts a letter, informing him that she would come to the hall and hold commercial talks with UDF if and only if the prince go and meet her via the K-th shortest path. (in fact, Uyuw does not want to come at all)"

Being interested in the trade development and such a lovely girl, Prince Remmarguts really became enamored. He needs you - the prime minister's help!

DETAILS: UDF's capital consists of N stations. The hall is numbered S, while the station numbered T denotes prince' current place. M muddy directed sideways connect some of the stations. Remmarguts' path to welcome the princess might include the same station twice or more than twice, even it is the station with number S or T. Different paths with same length will be considered disparate.

Input

The first line contains two integer numbers N and M (1 <= N <= 1000, 0 <= M <= 100000). Stations are numbered from 1 to N. Each of the following M lines contains three integer numbers A, B and T (1 <= A, B <= N, 1 <= T <= 100). It shows that there is a directed sideway from A-th station to B-th station with time T.

The last line consists of three integer numbers S, T and K (1 <= S, T <= N, 1 <= K <= 1000).

Output

A single line consisting of a single integer number: the length (time required) to welcome Princess Uyuw using the K-th shortest path. If K-th shortest path does not exist, you should output "-1" (without quotes) instead.

Sample Input

Sample Output

Source

POJ Monthly,Zeyuan Zhu

�W�K短�\问题�Q�大概意思就是给你N个点�Q�M条边�Q�边是有向的�Q�给你每条边的边权，�l�你一个S起始点，T�l�束点，和一个K�Q�求S到T的第K短�\�?br />SPFA+A*启发式搜索�?br />
说说启发式搜索吧�Q?br />

通常在解决问题的时候，我们需要用到搜索算法，由已知状态推出新的状态，然后��验新的状态是不是��是我们要求的最优解。检验完所有的状态实际上��q��当于遍历了一张隐式图。遗憄��是，所有的状态组成的状态空间往往是成指数�U�别增长的，也就造成了遍历需要用到指数��别的旉��Q�因此，�U��a的暴力搜索，时空效率都比较低。当�Ӟ��我们在生�z�M��遇到了类��g��搜烦的问题，我们�q�不会盲目地��L��L��一�U�状态，我们会通过我们的思维�Q�选择一条最接近于目标的路径或者是�q�似于最短的路径��d��成搜索�Q务。当我们惌��计算机去完成�q�样一��Ҏ��索�Q务的时候，��得让计��机像�h一栯��够区分尽量短的�\径，以便高效地找到最优解。这时可以把计算机看作是一�U�智能体(agent)可以实现由初始状态向目标状态的转移�?/span>

有一�U�贪心策略，��x��一步�{�U�都��p��机选择当前的最优解生成新的状态，一直到辄��标状态�ؓ止。这样做的时间效率虽然较高，但是贪心的策略只是用��C��局部的最优解�Q��ƈ不能保证最后到辄��标状态得到的是全局最优解。在能保证全局最优解的范围内�Q�贪心算法还是很有用的。比如说我们熟知�?/span>Dijkstra��法求单源最短�\。每�ơ选择距离源节�Ҏ��短距��ȝ��待扩展节点进行扩展，最后就能生成源节点到所有节点的最短�\径。下面会讲到Dijkstra的扩展，当理解了�q�个��法之后�Q�我惻I��你会�?/span>Dijkstra有更深入的理解�?/span>

�q�就�?/span>A*��法。定义初始状�?/span>S�Q�目标状�?/span>t�Q?/span>g(s)是由初始状态�{�U�d��当前状�?/span>s所�l�过的�\径长度，h*(s)是当前状�?/span>s距离目标状�?/span>t的实际长度，但是一般情况下我们是不知道h*(s)的值的�Q�所以还要定义一个估价函�?/span>h(s)�Q�是�?/span>h*(s)函数值的下界的估计，也就是有h(s)<=h*(s)�Q�这样需要一个条�Ӟ��使得�?/span>s1生成的每状�?/span>s2�Q�都�?/span>h(s1)<=h(s2)�Q�这是一个相容的��C�h函数。再定义f(s)=g(s)+h(s)为启发函敎ͼ�因�ؓh(s)是单调递增的，所�?/span>f(s)也是单调递增的。这�?/span>f(s)��׃��计出了由初始状态的��M��代�h�?/span>A*��法��通过构造这样一个启发函敎ͼ��所有的待扩展状态加入到队列里，每次从队列里选择f(s)值最��的状态进行扩展。由于启发函数的作用�Q��得计��机在进行状态�{�Uȝ��时候尽量避开了不可能产生最优解的分支，而选择相对较接�q�最优解的�\径进行搜索，提高了搜索效率�?/span>

讲到�q�里�Q�可能已�l�对A*��法的概忉|��点眉目了。下面我再来做一个比较，��q��上面讲到�?/span>Dijkstra的例子�?/span>Dijkstra��法说的是每�ơ选择距离源点最短距��ȝ��点进行扩展。当然可以看做事先将源点到所有节点距��ȝ��g��存在一个优先队列里�Q�每�ơ从优先队列里出队最短距��ȝ��Ҏ��展，每个点的扩展涉及到要更新队列里所有待扩展节点的距��d��|��每个节点只能�q�队一�ơ，��需要有一个表来记录每个节点的入队�ơ数�Q�就是算法中用到的标记数�l�）。将Dijkstra求最短�\的方法扩展，�q�道题目要求的是两点间第k短�\。类比于Dijkstra��法可以首先��定下面几个搜烦�{�略�Q?/span>

1�?/span>用优先队列保存节点进行搜索�?/span>

2�?/span>攑ּ�每个节点的入队次敎ͼ��?/span>k短�\�Q�每个节点可以入�?/span>k�ơ�?/span>

首先看第一个策略，�?/span>A*��法中用优先队列��是要用到启发函�?/span>f(s)��定状态在优先队列里面的优先��。其�?/span>Dijkstra用到的优先队列实际上��是��C�h函数��gؓ0�Q�启发函�?/span>f(s)=g(s)�Q�即是选取到源点距��L��q�的点进行扩展。因�?/span>h(s)=0满��了估价函数相容这个条件。这题求k短�\��׃��能单�U�的使用h(s)=0�q�个��C�h函数。解册��道题的时候选取h(x)=dt(x), dt(x)�?/span>x节点到目标节点的最短距��R��最短距��d��以开始由Dijkstra直接求得�?/span>

再看�W�二个策略，控制每个节点的入队（或出队）�ơ数�?/span>k�ơ，可以扑ֈ��W?/span>k短�\径。可能这��h��有点主观的套用，那么我就先来证明�q�样一个结论：

如果x�?/span>s�?/span>t的第k短�\径上的一个节点，那么��p��条�\�?/span>s�?/span>x�?/span>s�?/span>x的第m短�\径，则不可能�?/span>m>k。用反证法很�Ҏ��得出�Q�如果这条�\径是s�?/span>x的第m短�\径，如果m>k�Q�那么经�q?/span>x�?/span>t的�\径就�?/span>m-1条比当前路径要短�Q�不�W�合当前路径�?/span>s�?/span>t的第k短�\径�?br />

代码�Q?br />

#include <cstdio>
#include <algorithm>
#include <queue>
#include <vector>
#include <cstring>
#define MAXN 10005 //�Ҏ��
#define inf 1 << 25
using namespace std;

int dis[MAXN];

struct node
{
    int v, dis;
};

struct edge
{
    int v, w;
    friend bool operator < (edge a, edge b)
    {
        return (a.w + dis[a.v]) > (b.w + dis[b.v]);
    }
};

vector <node> map[MAXN];
vector <node> remap[MAXN];

int n, m; //n是节�Ҏ��Q�m是边数�?/span>
int s, t, k;  //s是�v始点�Q�t是结束点�Q�k是第k��?/span>

void init()
{
    int i;
    for (i = 0; i < MAXN; ++i)
        map[i].clear();
    for (i = 0; i < MAXN; ++i)
        remap[i].clear();
}

void spfa(int s)
{
    int i;
    bool used[MAXN];
    memset(used, 0, sizeof(used));
    for (i = 0; i < MAXN; ++i)
        dis[i] = inf;
    dis[s] = 0;
    used[s] = true;
    queue <int> q;
    q.push(s);
    while (!q.empty())
    {
        int u = q.front();
        q.pop();
        used[u] = false;
        for (i = 0; i < remap[u].size(); ++i)
        {
            node p = remap[u][i];
            if (dis[p.v] > dis[u] + p.dis)
            {
                dis[p.v] = dis[u] + p.dis;
                if (!used[p.v])
                {
                    used[p.v] = true;
                    q.push(p.v);
                }
            }
        }
    }
}

int a_star()
{
    if (s == t)
        k++;   //注意�Q��v始和�l�束一��P��k�?1�Q?/span>
    if (dis[s] == inf)
        return -1;
    int i, x, len, cnt[MAXN];
    edge n1, n2;
    priority_queue <edge> q;
    memset(cnt, 0, sizeof(cnt));
    n1.v = s;
    n1.w = 0;
    q.push(n1);
    while (!q.empty())
    {
        n2 = q.top();
        q.pop();
        x = n2.v;
        len = n2.w;
        cnt[x]++;
        if (cnt[t] == k)
            return len;
        if (cnt[x] > k)
            continue;
        for (i = 0; i < map[n2.v].size(); ++i)
        {
            n1.v = map[n2.v][i].v;
            n1.w = len + map[n2.v][i].dis;
            q.push(n1);
        }
    }
    return -1;
}

int main()
{
    int i;
    node p;
    while (scanf("%d%d", &n, &m) != EOF)
    {
        init();
        int a, b, l;
        for (i = 1; i <= m; ++i)
        {
            scanf("%d%d%d", &a, &b, &l);
            p.v = b;
            p.dis = l;
            map[a].push_back(p);
            p.v = a;
            remap[b].push_back(p);
        }
        scanf("%d%d%d", &s, &t, &k);
        spfa(t);
        int ans = a_star();
        printf("%d\n", ans);
    }
    return 0;
}

LLawliet 2011-10-17 15:19 发表评论