Taxi Cab Scheme

Description

Running a taxi station is not all that simple. Apart from the obvious demand for a centralised coordination of the cabs in order to pick up the customers calling to get a cab as soon as possible,there is also a need to schedule all the taxi rides which have been booked in advance.Given a list of all booked taxi rides for the next day, you want to minimise the number of cabs needed to carry out all of the rides.
For the sake of simplicity, we model a city as a rectangular grid. An address in the city is denoted by two integers: the street and avenue number. The time needed to get from the address a, b to c, d by taxi is |a - c| + |b - d| minutes. A cab may carry out a booked ride if it is its first ride of the day, or if it can get to the source address of the new ride from its latest,at least one minute before the new ride's scheduled departure. Note that some rides may end after midnight.

Input

On the first line of the input is a single positive integer N, telling the number of test scenarios to follow. Each scenario begins with a line containing an integer M, 0 < M < 500, being the number of booked taxi rides. The following M lines contain the rides. Each ride is described by a departure time on the format hh:mm (ranging from 00:00 to 23:59), two integers a b that are the coordinates of the source address and two integers c d that are the coordinates of the destination address. All coordinates are at least 0 and strictly smaller than 200. The booked rides in each scenario are sorted in order of increasing departure time.

Output

For each scenario, output one line containing the minimum number of cabs required to carry out all the booked taxi rides.

Sample Input

2

2

08:00 10 11 9 16

08:07 9 16 10 11

2

08:00 10 11 9 16

08:06 9 16 10 11

Sample Output

1

2

Source

Northwestern Europe 2004

       根據(jù)這道題目的意思，我們可以建一張圖，對(duì)于兩個(gè)booked taxi ride，ri和rj如果一輛車能夠先完成ri的任務(wù)再有時(shí)間趕去完成rj的任務(wù)，那么就建立一條ri指向rj的邊。

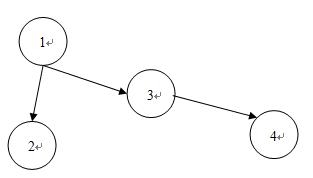
       按照題目的要求，要選擇最少的taxi來(lái)完成這些任務(wù)。顯然在上面這個(gè)例子中，需要安排2輛taxi。結(jié)合這個(gè)圖，可以把題目的要求轉(zhuǎn)化為找出最少的路徑條數(shù)，使得這些路徑覆蓋途中所有的邊，例如可以選擇2條路徑1->3->4和1->2就可以覆蓋所有的邊。也可以選擇1->3->4和2（因?yàn)?/span>2作為初始站，不需要由1轉(zhuǎn)移過(guò)來(lái)）。對(duì)于一條連續(xù)的路徑vi1->vi2->…vik由于這條路徑上的任務(wù)實(shí)際上是由一輛taxi來(lái)完成的，可以吧這條路徑退化成兩個(gè)點(diǎn)vi1->vik。有了這兩步建圖的步驟以后，問(wèn)題的求解就可以變?yōu)檎页鲰旤c(diǎn)集的一個(gè)最小子集，使這個(gè)頂點(diǎn)子集覆蓋所有的邊（每條邊都至少和一個(gè)頂點(diǎn)集的頂點(diǎn)相連）。這個(gè)問(wèn)題就是圖的最小點(diǎn)覆蓋。再看這張圖，還有一些性質(zhì)能夠讓我們更好地求出最小點(diǎn)覆蓋。這個(gè)圖是一個(gè)有向無(wú)環(huán)圖，沒(méi)有自環(huán)，就可以拆點(diǎn)，把原先建的圖變成一張二分圖。

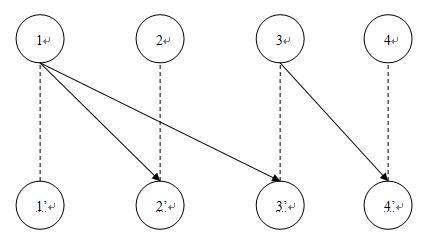
可以再圖中看出，上面舉出的一條路徑1->3->4對(duì)應(yīng)了這個(gè)二分圖中的路徑1->3’->3->4’，在這個(gè)二分圖中就需要求一個(gè)最大獨(dú)立子集（這里的4點(diǎn)就是一條路徑的終點(diǎn)，沒(méi)一條路徑即對(duì)應(yīng)有一個(gè)終點(diǎn)！）。二分圖的最大獨(dú)立數(shù)是總點(diǎn)數(shù)與最大匹配數(shù)的差值。接下來(lái)建圖，拆點(diǎn)，求二分圖最大匹配就能解決這道題目了。

 1#include <stdio.h>
 2#include <string.h>
 3#include <algorithm>
 4using namespace std;
 5
 6struct Point
 7{
 8    int x,y;
 9};
10struct P
11{
12    int s,e;
13    struct Point s1,s2;
14}p[505];
15int n,g[505][505],match[505];
16bool chk[505];
17
18/**//*int abs(int a)
19{
20    return a < 0 ? -a : a;
21}*/
22bool operator <(const P a, const P b)
23{
24    return a.s < b.s;
25}
26int dfs(int v)
27{
28    int i,t;
29    for(i=0; i<n; i++)
30    {
31        if(!chk[i] && g[v][i])
32        {
33            t=match[i];
34            chk[i]=true;
35            match[i]=v;
36            if(t == -1 || dfs(t)) return 1;
37            match[i]=t;
38        }
39    }
40    return 0;
41}
42int Twomatch()
43{
44    int i,ans=0;
45    memset(match,-1,sizeof(match));
46    for(i=0; i<n; i++)
47    {
48        memset(chk,false,sizeof(chk));
49        if(dfs(i)) ans++;
50    }
51    return ans;
52}
53
54int main()
55{
56    int i,cases,a,b,j,cnt;
57    char temp[10];
58    //freopen("in.txt","r",stdin);
59    scanf("%d",&cases);
60    while(cases--)
61    {
62        scanf("%d",&n);
63
64        for(i=0; i<n; i++)
65        {
66            scanf("%s",temp);
67            scanf("%d%d%d%d",&p[i].s1.x,&p[i].s1.y,&p[i].s2.x,&p[i].s2.y);
68            sscanf(temp,"%d%*[:]%d",&a,&b);
69            p[i].s=a*60+b;
70            p[i].e=p[i].s+abs(p[i].s2.x-p[i].s1.x)+abs(p[i].s2.y-p[i].s1.y);
71        }
72        //sort(p,p+n);
73        cnt=0;
74        memset(g,0,sizeof(g));
75        for(i=0; i<n; i++)
76        {
77            for(j=0; j<n; j++)
78            {
79                if(p[i].e+abs(p[i].s2.x-p[j].s1.x)+abs(p[i].s2.y-p[j].s1.y) < p[j].s && i != j)
80                    g[i][j]=1;
81            }
82        }
83        printf("%d\n",n-Twomatch());
84    }
85    return 0;
86}
87