1. 給定a、b兩個(gè)文件,各存放50億個(gè)url,每個(gè)url各占64字節(jié),內(nèi)存限制是4G,讓你找出a、b文件共同的url?
方案1:可以估計(jì)每個(gè)文件安的大小為50G×64=320G,遠(yuǎn)遠(yuǎn)大于內(nèi)存限制的4G。所以不可能將其完全加載到內(nèi)存中處理。考慮采取分而治之的方法。
s 遍歷文件a,對每個(gè)url求取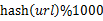 ,然后根據(jù)所取得的值將url分別存儲到1000個(gè)小文件(記為
,然后根據(jù)所取得的值將url分別存儲到1000個(gè)小文件(記為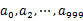 )中。這樣每個(gè)小文件的大約為300M。
)中。這樣每個(gè)小文件的大約為300M。
s 遍歷文件b,采取和a相同的方式將url分別存儲到1000各小文件(記為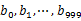 )。這樣處理后,所有可能相同的url都在對應(yīng)的小文件(
)。這樣處理后,所有可能相同的url都在對應(yīng)的小文件(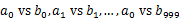 )中,不對應(yīng)的小文件不可能有相同的url。然后我們只要求出1000對小文件中相同的url即可。
)中,不對應(yīng)的小文件不可能有相同的url。然后我們只要求出1000對小文件中相同的url即可。
s 求每對小文件中相同的url時(shí),可以把其中一個(gè)小文件的url存儲到hash_set中。然后遍歷另一個(gè)小文件的每個(gè)url,看其是否在剛才構(gòu)建的hash_set中,如果是,那么就是共同的url,存到文件里面就可以了。
方案2:如果允許有一定的錯(cuò)誤率,可以使用Bloom filter,4G內(nèi)存大概可以表示340億bit。將其中一個(gè)文件中的url使用Bloom filter映射為這340億bit,然后挨個(gè)讀取另外一個(gè)文件的url,檢查是否與Bloom filter,如果是,那么該url應(yīng)該是共同的url(注意會有一定的錯(cuò)誤率)。
2. 有10個(gè)文件,每個(gè)文件1G,每個(gè)文件的每一行存放的都是用戶的query,每個(gè)文件的query都可能重復(fù)。要求你按照query的頻度排序。
方案1:
s 順序讀取10個(gè)文件,按照hash(query)%10的結(jié)果將query寫入到另外10個(gè)文件(記為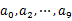 )中。這樣新生成的文件每個(gè)的大小大約也1G(假設(shè)hash函數(shù)是隨機(jī)的)。
)中。這樣新生成的文件每個(gè)的大小大約也1G(假設(shè)hash函數(shù)是隨機(jī)的)。
s 找一臺內(nèi)存在2G左右的機(jī)器,依次對![clip_image010[1] clip_image010[1]](http://images.cnblogs.com/cnblogs_com/youwang/WindowsLiveWriter/1340f2e6fa8e_D5D1/clip_image010%5B1%5D_thumb.png) 用hash_map(query, query_count)來統(tǒng)計(jì)每個(gè)query出現(xiàn)的次數(shù)。利用快速/堆/歸并排序按照出現(xiàn)次數(shù)進(jìn)行排序。將排序好的query和對應(yīng)的query_cout輸出到文件中。這樣得到了10個(gè)排好序的文件(記為
用hash_map(query, query_count)來統(tǒng)計(jì)每個(gè)query出現(xiàn)的次數(shù)。利用快速/堆/歸并排序按照出現(xiàn)次數(shù)進(jìn)行排序。將排序好的query和對應(yīng)的query_cout輸出到文件中。這樣得到了10個(gè)排好序的文件(記為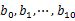 )。
)。
s 對![clip_image012[1] clip_image012[1]](http://images.cnblogs.com/cnblogs_com/youwang/WindowsLiveWriter/1340f2e6fa8e_D5D1/clip_image012%5B1%5D_thumb.png) 這10個(gè)文件進(jìn)行歸并排序(內(nèi)排序與外排序相結(jié)合)。
這10個(gè)文件進(jìn)行歸并排序(內(nèi)排序與外排序相結(jié)合)。
方案2:
一般query的總量是有限的,只是重復(fù)的次數(shù)比較多而已,可能對于所有的query,一次性就可以加入到內(nèi)存了。這樣,我們就可以采用trie樹/hash_map等直接來統(tǒng)計(jì)每個(gè)query出現(xiàn)的次數(shù),然后按出現(xiàn)次數(shù)做快速/堆/歸并排序就可以了。
方案3:
與方案1類似,但在做完hash,分成多個(gè)文件后,可以交給多個(gè)文件來處理,采用分布式的架構(gòu)來處理(比如MapReduce),最后再進(jìn)行合并。
3. 有一個(gè)1G大小的一個(gè)文件,里面每一行是一個(gè)詞,詞的大小不超過16字節(jié),內(nèi)存限制大小是1M。返回頻數(shù)最高的100個(gè)詞。
方案1:順序讀文件中,對于每個(gè)詞x,取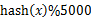 ,然后按照該值存到5000個(gè)小文件(記為
,然后按照該值存到5000個(gè)小文件(記為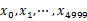 )中。這樣每個(gè)文件大概是200k左右。如果其中的有的文件超過了1M大小,還可以按照類似的方法繼續(xù)往下分,知道分解得到的小文件的大小都不超過1M。對每個(gè)小文件,統(tǒng)計(jì)每個(gè)文件中出現(xiàn)的詞以及相應(yīng)的頻率(可以采用trie樹/hash_map等),并取出出現(xiàn)頻率最大的100個(gè)詞(可以用含100個(gè)結(jié)點(diǎn)的最小堆),并把100詞及相應(yīng)的頻率存入文件,這樣又得到了5000個(gè)文件。下一步就是把這5000個(gè)文件進(jìn)行歸并(類似與歸并排序)的過程了。
)中。這樣每個(gè)文件大概是200k左右。如果其中的有的文件超過了1M大小,還可以按照類似的方法繼續(xù)往下分,知道分解得到的小文件的大小都不超過1M。對每個(gè)小文件,統(tǒng)計(jì)每個(gè)文件中出現(xiàn)的詞以及相應(yīng)的頻率(可以采用trie樹/hash_map等),并取出出現(xiàn)頻率最大的100個(gè)詞(可以用含100個(gè)結(jié)點(diǎn)的最小堆),并把100詞及相應(yīng)的頻率存入文件,這樣又得到了5000個(gè)文件。下一步就是把這5000個(gè)文件進(jìn)行歸并(類似與歸并排序)的過程了。
4. 海量日志數(shù)據(jù),提取出某日訪問百度次數(shù)最多的那個(gè)IP。
方案1:首先是這一天,并且是訪問百度的日志中的IP取出來,逐個(gè)寫入到一個(gè)大文件中。注意到IP是32位的,最多有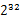 個(gè)IP。同樣可以采用映射的方法,比如模1000,把整個(gè)大文件映射為1000個(gè)小文件,再找出每個(gè)小文中出現(xiàn)頻率最大的IP(可以采用hash_map進(jìn)行頻率統(tǒng)計(jì),然后再找出頻率最大的幾個(gè))及相應(yīng)的頻率。然后再在這1000個(gè)最大的IP中,找出那個(gè)頻率最大的IP,即為所求。
個(gè)IP。同樣可以采用映射的方法,比如模1000,把整個(gè)大文件映射為1000個(gè)小文件,再找出每個(gè)小文中出現(xiàn)頻率最大的IP(可以采用hash_map進(jìn)行頻率統(tǒng)計(jì),然后再找出頻率最大的幾個(gè))及相應(yīng)的頻率。然后再在這1000個(gè)最大的IP中,找出那個(gè)頻率最大的IP,即為所求。
5. 在2.5億個(gè)整數(shù)中找出不重復(fù)的整數(shù),內(nèi)存不足以容納這2.5億個(gè)整數(shù)。
方案1:采用2-Bitmap(每個(gè)數(shù)分配2bit,00表示不存在,01表示出現(xiàn)一次,10表示多次,11無意義)進(jìn)行,共需內(nèi)存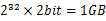 內(nèi)存,還可以接受。然后掃描這2.5億個(gè)整數(shù),查看Bitmap中相對應(yīng)位,如果是00變01,01變10,10保持不變。所描完事后,查看bitmap,把對應(yīng)位是01的整數(shù)輸出即可。
內(nèi)存,還可以接受。然后掃描這2.5億個(gè)整數(shù),查看Bitmap中相對應(yīng)位,如果是00變01,01變10,10保持不變。所描完事后,查看bitmap,把對應(yīng)位是01的整數(shù)輸出即可。
方案2:也可采用上題類似的方法,進(jìn)行劃分小文件的方法。然后在小文件中找出不重復(fù)的整數(shù),并排序。然后再進(jìn)行歸并,注意去除重復(fù)的元素。
6. 海量數(shù)據(jù)分布在100臺電腦中,想個(gè)辦法高校統(tǒng)計(jì)出這批數(shù)據(jù)的TOP10。
方案1:
s 在每臺電腦上求出TOP10,可以采用包含10個(gè)元素的堆完成(TOP10小,用最大堆,TOP10大,用最小堆)。比如求TOP10大,我們首先取前10個(gè)元素調(diào)整成最小堆,如果發(fā)現(xiàn),然后掃描后面的數(shù)據(jù),并與堆頂元素比較,如果比堆頂元素大,那么用該元素替換堆頂,然后再調(diào)整為最小堆。最后堆中的元素就是TOP10大。
s 求出每臺電腦上的TOP10后,然后把這100臺電腦上的TOP10組合起來,共1000個(gè)數(shù)據(jù),再利用上面類似的方法求出TOP10就可以了。
7. 怎么在海量數(shù)據(jù)中找出重復(fù)次數(shù)最多的一個(gè)?
方案1:先做hash,然后求模映射為小文件,求出每個(gè)小文件中重復(fù)次數(shù)最多的一個(gè),并記錄重復(fù)次數(shù)。然后找出上一步求出的數(shù)據(jù)中重復(fù)次數(shù)最多的一個(gè)就是所求(具體參考前面的題)。
8. 上千萬或上億數(shù)據(jù)(有重復(fù)),統(tǒng)計(jì)其中出現(xiàn)次數(shù)最多的錢N個(gè)數(shù)據(jù)。
方案1:上千萬或上億的數(shù)據(jù),現(xiàn)在的機(jī)器的內(nèi)存應(yīng)該能存下。所以考慮采用hash_map/搜索二叉樹/紅黑樹等來進(jìn)行統(tǒng)計(jì)次數(shù)。然后就是取出前N個(gè)出現(xiàn)次數(shù)最多的數(shù)據(jù)了,可以用第6題提到的堆機(jī)制完成。
9. 1000萬字符串,其中有些是重復(fù)的,需要把重復(fù)的全部去掉,保留沒有重復(fù)的字符串。請?jiān)趺丛O(shè)計(jì)和實(shí)現(xiàn)?
方案1:這題用trie樹比較合適,hash_map也應(yīng)該能行。
10. 一個(gè)文本文件,大約有一萬行,每行一個(gè)詞,要求統(tǒng)計(jì)出其中最頻繁出現(xiàn)的前10個(gè)詞,請給出思想,給出時(shí)間復(fù)雜度分析。
方案1:這題是考慮時(shí)間效率。用trie樹統(tǒng)計(jì)每個(gè)詞出現(xiàn)的次數(shù),時(shí)間復(fù)雜度是O(n*le)(le表示單詞的平準(zhǔn)長度)。然后是找出出現(xiàn)最頻繁的前10個(gè)詞,可以用堆來實(shí)現(xiàn),前面的題中已經(jīng)講到了,時(shí)間復(fù)雜度是O(n*lg10)。所以總的時(shí)間復(fù)雜度,是O(n*le)與O(n*lg10)中較大的哪一個(gè)。
11. 一個(gè)文本文件,找出前10個(gè)經(jīng)常出現(xiàn)的詞,但這次文件比較長,說是上億行或十億行,總之無法一次讀入內(nèi)存,問最優(yōu)解。
方案1:首先根據(jù)用hash并求模,將文件分解為多個(gè)小文件,對于單個(gè)文件利用上題的方法求出每個(gè)文件件中10個(gè)最常出現(xiàn)的詞。然后再進(jìn)行歸并處理,找出最終的10個(gè)最常出現(xiàn)的詞。
12. 100w個(gè)數(shù)中找出最大的100個(gè)數(shù)。
方案1:在前面的題中,我們已經(jīng)提到了,用一個(gè)含100個(gè)元素的最小堆完成。復(fù)雜度為O(100w*lg100)。
方案2:采用快速排序的思想,每次分割之后只考慮比軸大的一部分,知道比軸大的一部分在比100多的時(shí)候,采用傳統(tǒng)排序算法排序,取前100個(gè)。復(fù)雜度為O(100w*100)。
方案3:采用局部淘汰法。選取前100個(gè)元素,并排序,記為序列L。然后一次掃描剩余的元素x,與排好序的100個(gè)元素中最小的元素比,如果比這個(gè)最小的要大,那么把這個(gè)最小的元素刪除,并把x利用插入排序的思想,插入到序列L中。依次循環(huán),知道掃描了所有的元素。復(fù)雜度為O(100w*100)。
13. 尋找熱門查詢:
搜索引擎會通過日志文件把用戶每次檢索使用的所有檢索串都記錄下來,每個(gè)查詢串的長度為1-255字節(jié)。假設(shè)目前有一千萬個(gè)記錄,這些查詢串的重復(fù)讀比較高,雖然總數(shù)是1千萬,但是如果去除重復(fù)和,不超過3百萬個(gè)。一個(gè)查詢串的重復(fù)度越高,說明查詢它的用戶越多,也就越熱門。請你統(tǒng)計(jì)最熱門的10個(gè)查詢串,要求使用的內(nèi)存不能超過1G。
(1) 請描述你解決這個(gè)問題的思路;
(2) 請給出主要的處理流程,算法,以及算法的復(fù)雜度。
方案1:采用trie樹,關(guān)鍵字域存該查詢串出現(xiàn)的次數(shù),沒有出現(xiàn)為0。最后用10個(gè)元素的最小推來對出現(xiàn)頻率進(jìn)行排序。
14. 一共有N個(gè)機(jī)器,每個(gè)機(jī)器上有N個(gè)數(shù)。每個(gè)機(jī)器最多存O(N)個(gè)數(shù)并對它們操作。如何找到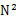 個(gè)數(shù)中的中數(shù)?
個(gè)數(shù)中的中數(shù)?
方案1:先大體估計(jì)一下這些數(shù)的范圍,比如這里假設(shè)這些數(shù)都是32位無符號整數(shù)(共有![clip_image018[1] clip_image018[1]](http://images.cnblogs.com/cnblogs_com/youwang/WindowsLiveWriter/1340f2e6fa8e_D5D1/clip_image018%5B1%5D_thumb.png) 個(gè))。我們把0到
個(gè))。我們把0到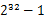 的整數(shù)劃分為N個(gè)范圍段,每個(gè)段包含
的整數(shù)劃分為N個(gè)范圍段,每個(gè)段包含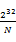 個(gè)整數(shù)。比如,第一個(gè)段位0到
個(gè)整數(shù)。比如,第一個(gè)段位0到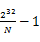 ,第二段為
,第二段為![clip_image026[1] clip_image026[1]](http://images.cnblogs.com/cnblogs_com/youwang/WindowsLiveWriter/1340f2e6fa8e_D5D1/clip_image026%5B1%5D_thumb.png) 到
到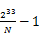 ,…,第N個(gè)段為
,…,第N個(gè)段為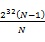 到
到![clip_image024[1] clip_image024[1]](http://images.cnblogs.com/cnblogs_com/youwang/WindowsLiveWriter/1340f2e6fa8e_D5D1/clip_image024%5B1%5D_thumb.png) 。然后,掃描每個(gè)機(jī)器上的N個(gè)數(shù),把屬于第一個(gè)區(qū)段的數(shù)放到第一個(gè)機(jī)器上,屬于第二個(gè)區(qū)段的數(shù)放到第二個(gè)機(jī)器上,…,屬于第N個(gè)區(qū)段的數(shù)放到第N個(gè)機(jī)器上。注意這個(gè)過程每個(gè)機(jī)器上存儲的數(shù)應(yīng)該是O(N)的。下面我們依次統(tǒng)計(jì)每個(gè)機(jī)器上數(shù)的個(gè)數(shù),一次累加,直到找到第k個(gè)機(jī)器,在該機(jī)器上累加的數(shù)大于或等于
。然后,掃描每個(gè)機(jī)器上的N個(gè)數(shù),把屬于第一個(gè)區(qū)段的數(shù)放到第一個(gè)機(jī)器上,屬于第二個(gè)區(qū)段的數(shù)放到第二個(gè)機(jī)器上,…,屬于第N個(gè)區(qū)段的數(shù)放到第N個(gè)機(jī)器上。注意這個(gè)過程每個(gè)機(jī)器上存儲的數(shù)應(yīng)該是O(N)的。下面我們依次統(tǒng)計(jì)每個(gè)機(jī)器上數(shù)的個(gè)數(shù),一次累加,直到找到第k個(gè)機(jī)器,在該機(jī)器上累加的數(shù)大于或等于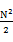 ,而在第k-1個(gè)機(jī)器上的累加數(shù)小于
,而在第k-1個(gè)機(jī)器上的累加數(shù)小于![clip_image034[1] clip_image034[1]](http://images.cnblogs.com/cnblogs_com/youwang/WindowsLiveWriter/1340f2e6fa8e_D5D1/clip_image034%5B1%5D_thumb.png) ,并把這個(gè)數(shù)記為x。那么我們要找的中位數(shù)在第k個(gè)機(jī)器中,排在第
,并把這個(gè)數(shù)記為x。那么我們要找的中位數(shù)在第k個(gè)機(jī)器中,排在第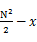 位。然后我們對第k個(gè)機(jī)器的數(shù)排序,并找出第
位。然后我們對第k個(gè)機(jī)器的數(shù)排序,并找出第![clip_image036[1] clip_image036[1]](http://images.cnblogs.com/cnblogs_com/youwang/WindowsLiveWriter/1340f2e6fa8e_D5D1/clip_image036%5B1%5D_thumb.png) 個(gè)數(shù),即為所求的中位數(shù)。復(fù)雜度是
個(gè)數(shù),即為所求的中位數(shù)。復(fù)雜度是 的。
的。
方案2:先對每臺機(jī)器上的數(shù)進(jìn)行排序。排好序后,我們采用歸并排序的思想,將這N個(gè)機(jī)器上的數(shù)歸并起來得到最終的排序。找到第![clip_image034[2] clip_image034[2]](http://images.cnblogs.com/cnblogs_com/youwang/WindowsLiveWriter/1340f2e6fa8e_D5D1/clip_image034%5B2%5D_thumb.png) 個(gè)便是所求。復(fù)雜度是
個(gè)便是所求。復(fù)雜度是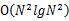 的。
的。
15. 最大間隙問題
給定n個(gè)實(shí)數(shù)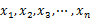 ,求著n個(gè)實(shí)數(shù)在實(shí)軸上向量2個(gè)數(shù)之間的最大差值,要求線性的時(shí)間算法。
,求著n個(gè)實(shí)數(shù)在實(shí)軸上向量2個(gè)數(shù)之間的最大差值,要求線性的時(shí)間算法。
方案1:最先想到的方法就是先對這n個(gè)數(shù)據(jù)進(jìn)行排序,然后一遍掃描即可確定相鄰的最大間隙。但該方法不能滿足線性時(shí)間的要求。故采取如下方法:
s 找到n個(gè)數(shù)據(jù)中最大和最小數(shù)據(jù)max和min。
s 用n-2個(gè)點(diǎn)等分區(qū)間[min, max],即將[min, max]等分為n-1個(gè)區(qū)間(前閉后開區(qū)間),將這些區(qū)間看作桶,編號為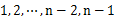 ,且桶
,且桶 的上界和桶i+1的下屆相同,即每個(gè)桶的大小相同。每個(gè)桶的大小為:
的上界和桶i+1的下屆相同,即每個(gè)桶的大小相同。每個(gè)桶的大小為: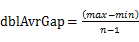 。實(shí)際上,這些桶的邊界構(gòu)成了一個(gè)等差數(shù)列(首項(xiàng)為min,公差為
。實(shí)際上,這些桶的邊界構(gòu)成了一個(gè)等差數(shù)列(首項(xiàng)為min,公差為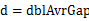 ),且認(rèn)為將min放入第一個(gè)桶,將max放入第n-1個(gè)桶。
),且認(rèn)為將min放入第一個(gè)桶,將max放入第n-1個(gè)桶。
s 將n個(gè)數(shù)放入n-1個(gè)桶中:將每個(gè)元素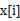 分配到某個(gè)桶(編號為index),其中
分配到某個(gè)桶(編號為index),其中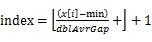 ,并求出分到每個(gè)桶的最大最小數(shù)據(jù)。
,并求出分到每個(gè)桶的最大最小數(shù)據(jù)。
s 最大間隙:除最大最小數(shù)據(jù)max和min以外的n-2個(gè)數(shù)據(jù)放入n-1個(gè)桶中,由抽屜原理可知至少有一個(gè)桶是空的,又因?yàn)槊總€(gè)桶的大小相同,所以最大間隙不會在同一桶中出現(xiàn),一定是某個(gè)桶的上界和氣候某個(gè)桶的下界之間隙,且該量筒之間的桶(即便好在該連個(gè)便好之間的桶)一定是空桶。也就是說,最大間隙在桶i的上界和桶j的下界之間產(chǎn)生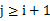 。一遍掃描即可完成。
。一遍掃描即可完成。
16. 將多個(gè)集合合并成沒有交集的集合:給定一個(gè)字符串的集合,格式如: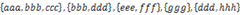 。要求將其中交集不為空的集合合并,要求合并完成的集合之間無交集,例如上例應(yīng)輸出
。要求將其中交集不為空的集合合并,要求合并完成的集合之間無交集,例如上例應(yīng)輸出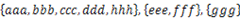 。
。
(1) 請描述你解決這個(gè)問題的思路;
(2) 給出主要的處理流程,算法,以及算法的復(fù)雜度;
(3) 請描述可能的改進(jìn)。
方案1:采用并查集。首先所有的字符串都在單獨(dú)的并查集中。然后依掃描每個(gè)集合,順序合并將兩個(gè)相鄰元素合并。例如,對于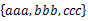 ,首先查看aaa和bbb是否在同一個(gè)并查集中,如果不在,那么把它們所在的并查集合并,然后再看bbb和ccc是否在同一個(gè)并查集中,如果不在,那么也把它們所在的并查集合并。接下來再掃描其他的集合,當(dāng)所有的集合都掃描完了,并查集代表的集合便是所求。復(fù)雜度應(yīng)該是O(NlgN)的。改進(jìn)的話,首先可以記錄每個(gè)節(jié)點(diǎn)的根結(jié)點(diǎn),改進(jìn)查詢。合并的時(shí)候,可以把大的和小的進(jìn)行合,這樣也減少復(fù)雜度。
,首先查看aaa和bbb是否在同一個(gè)并查集中,如果不在,那么把它們所在的并查集合并,然后再看bbb和ccc是否在同一個(gè)并查集中,如果不在,那么也把它們所在的并查集合并。接下來再掃描其他的集合,當(dāng)所有的集合都掃描完了,并查集代表的集合便是所求。復(fù)雜度應(yīng)該是O(NlgN)的。改進(jìn)的話,首先可以記錄每個(gè)節(jié)點(diǎn)的根結(jié)點(diǎn),改進(jìn)查詢。合并的時(shí)候,可以把大的和小的進(jìn)行合,這樣也減少復(fù)雜度。
17. 最大子序列與最大子矩陣問題
數(shù)組的最大子序列問題:給定一個(gè)數(shù)組,其中元素有正,也有負(fù),找出其中一個(gè)連續(xù)子序列,使和最大。
方案1:這個(gè)問題可以動態(tài)規(guī)劃的思想解決。設(shè)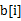 表示以第i個(gè)元素
表示以第i個(gè)元素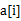 結(jié)尾的最大子序列,那么顯然
結(jié)尾的最大子序列,那么顯然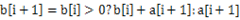 。基于這一點(diǎn)可以很快用代碼實(shí)現(xiàn)。
。基于這一點(diǎn)可以很快用代碼實(shí)現(xiàn)。
最大子矩陣問題:給定一個(gè)矩陣(二維數(shù)組),其中數(shù)據(jù)有大有小,請找一個(gè)子矩陣,使得子矩陣的和最大,并輸出這個(gè)和。
方案1:可以采用與最大子序列類似的思想來解決。如果我們確定了選擇第i列和第j列之間的元素,那么在這個(gè)范圍內(nèi),其實(shí)就是一個(gè)最大子序列問題。如何確定第i列和第j列可以詞用暴搜的方法進(jìn)行。